nLab AdS-CFT in condensed matter physics

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Discuss this page |
Contents

Context

Solid state physics

String theory

Ingredients

Critical string models

Extended objects

Topological strings

Backgrounds

Phenomenology

Contents

Idea

The AdS-CFT correspondence applies exactly only to a few highly symmetric quantum field theories, notably to N=4 D=4 super Yang-Mills theory. However, it still applies in adjusted form when moving away from these special points in field theory space (e.g Park 2022).

For instance quantum chromodynamics (one sector of the standard model of particle physics) is crucially different from but still similar enough to N=4 D=4 super Yang-Mills theory that some of its observables, in particular otherwise intractable non-perturbative effects, have been argued to be usefully approximated by AdS-CFT-type dual gravity-observables, for instance the shear viscosity of the quark-gluon plasma. This is hence also called the AdS/QCD correspondence.

Similarly, as far as systems in condensed matter physics are described well by some effective field theory, one may ask whether this, in turn, is usefully related to gravity on some anti de-Sitter spacetime and use this to study the solid state system, notably its non-perturbative effects. This area goes under the name AdS/CMT.

Andreas Karch writes here:

These anomalous transport coefficients have first been calculated in AdS/CFT. The relevant references are [8], [9] and [10] in the Son/Surowka paper. In the AdS/CFT calculations these particular transport coefficients only arise due to Chern-Simons terms, which are the bulk manifestation of the field theory anomalies. At that point it was obvious to many of us that there should be a purely field theory based calculation, only using anomalies, that can derive these terms. Son and Surowka knew about this. They were sitting next door to me when they started these calculations. Many of us tried to find these purely field theory based arguments and failed. Son and Surowka succeeded.

If you ask anyone serious about applying AdS/CFT to strongly coupled field theories why they are doing this, they would (hopefully) give you an answer along the lines of “AdS/CFT provides us with toy models of strongly coupled dynamics. While the field theories that have classical AdS duals are rather special, we can still learn important qualitative insights and find new ways to think about strongly coupled field theories.” Once AdS/CFT stumbles on a new phenomenon in these solvable toy models, we want to go back to see whether we can understand it without the crutch of having to rely on AdS/CFT. Any result that only applies in theories with holographic dual is somewhat limited in its applications. In this sense, anomalous transport is a poster child for what AdS/CFT can be used for: a new phenomenon that had been missed completely by people studying field theory gets uncovered by studying these toy models. Once we knew what to look for, a purely field theoretic argument was found that made the AdS/CFT derivation obsolete.

This is applied AdS/CFT as it should be. Solvable examples exhibit new connections which then can be proven to be correct more generally and are not limited to the toy models that were used to uncover them.

Similarly Hartnoll, Lucas & Sachdev 2016, p. 8:

Our main objective here is to make clear that explicit examples of the duality are known in various dimensions and that they are found by using string theory as a bridge between quantum field theory and gravity.

Properties

Description by tensor networks

Discussion of renormalization and entangled states of non-perturbative effects in solid state physics proceeds via tensor networks (Swingle 09, Swingle 13) and the resulting discovery of the relation to holographic entanglement entropy.

In this context, a tensor network is a string diagram with an attitude, in that it is (just) a string diagram, but with

  1. the tensor product of all its external objects regarded as a space of states of a quantum system;

  2. the element in that tensor product defined by the string diagram regarded a a state (wave function) of that quantum system.

For instance, if 𝔤\mathfrak{g} is a metric Lie algebra (with string diagram-notation as shown there), and with each tensor product-power of its dual vector space regarded as Hilbert space, hence as a space of quantum states, via the given inner product on 𝔤\mathfrak{g}, then an example of a tree tensor network state is the following:

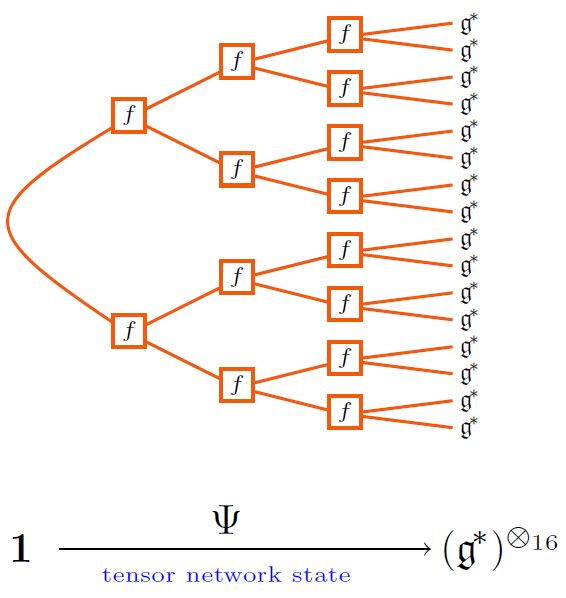
The quantum states arising this way are generically highly entangled: roughly they are the more entangled the more vertices there are in the corresponding tensor network.

Tree tensor network states in the form of Bruhat-Tits trees play a special role in the AdS/CFT correspondence, either as

  1. a kind of lattice QFT-approximation to an actual boundary CFT quantum state,

  2. as the p-adic geometric incarnation of anti de Sitter spacetime in the p-adic AdS/CFT correspondence,

  3. as a reflection of actual crystal-site quantum states in AdS/CFT in solid state physics:

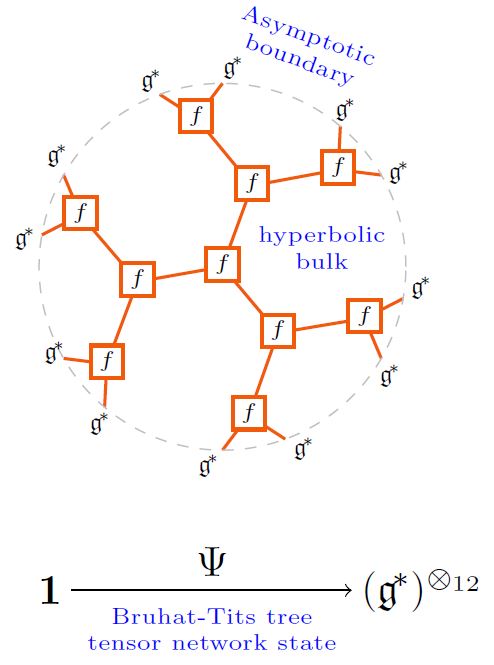
graphics from Sati-Schreiber 19c

For Bruhat-Tits tree tensor network states one finds that the holographic entanglement entropy of the tensor subspace associated with an interval on the boundary becomes proportional, for large number of vertices, to the hyperbolic bulk boundary length of the segment of the tree network that ends on this interval, according to the Ryu-Takayanagi formula (PYHP 15, Theorem 2). For more on this see below.

References

General

The original article (according to ZLSS15, p. ix), regarding AdS4/CFT3-duality (hence with the bulk theory being 11d supergravity, whence “M-theory”) as a tool for understanding strongly coupled condensed matter physics (specifically superconductivity):

and further discussion along these lines (for more referenceson holographic superconductors see below):

Monographs:

Reviews and lectures:

See also:

On Lifshitz holography relevant fordescribing disorder systems:

  • Chanyong Park, Holographic two-point functions in a disorder system [arXiv:2209.07721]

On holographic description of phonon gases in non-merallic crystals:

  • Xiangqing Kong, Tao Wang, Liu Zhao, High temperature AdS black holes are low temperature quantum phonon gases [arXiv:2209.12230]

On holographic description of quantum spin chains:

  • Naoto Yokoi, Yasuyuki Oikawa, Eiji Saitoh, Holographic Dual of Quantum Spin Chain as Chern-Simons-Scalar Theory [arXiv:2310.01890]

On phase transitions:

Via supergravity

Usage of full supergravity (retaining the gravitino) for AdS-CMT, with application to graphene-like systems:

Exposition:

Background discussion of supergravity with asymptotic boundaries (in the D'Auria-Fré formulation):

See also

Application to (strange) metals

More on application to (strange) metals:

Application to topological phases of matter

On holographic descriptions of topological semimetals via the AdS-CMT correspondence:

Review:

Application to band structure

Application to electron band structure of multi-layer graphene:

  • Jeong-Won Seo, Taewon Yuk, Young-Kwon Han, Sang-Jin Sin, ABC-stacked multilayer graphene in holography [arXiv:2208.14642]

Application to quantum chromodynamics

Discussion of quantum chromodynamics via AdS/CFT in condensed matter physics (see also at AdS/QCD):

Application to BEC and superfluidity

Application to Bose-Einstein condensates, superfluidity and vortices:

  • Yu-Kun Yan, Shanquan Lan, Yu Tian, Peng Yang, Shunhui Yao, Hongbao Zhang, Towards an effective description of holographic vortex dynamics [arXiv:2207.02814]

  • Aristomenis Donos, Polydoros Kailidis, Dissipative effects in finite density holographic superfluids [arXiv:2209.06893]

  • Mario Flory, Sebastian Grieninger, Sergio Morales-Tejera, Critical and near-critical relaxation of holographic superfluids [arXiv:2209.09251]

  • Markus A. G. Amano, Minoru Eto, Holographic Global Vortices with Novel Boundary Conditions [arXiv:2404.03212]

  • Zi-Qiang Zhao, Zhang-Yu Nie, Jing-Fei Zhang, Xin Zhang, Matteo Baggioli, Dynamical and thermodynamic crossovers in the supercritical region of a holographic superfluid model [arXiv:2406.05345]

  • Meng Gao, Zhuan Ning, Yu Tian, Hongbao Zhang: Holographic homogeneous superfluid on the sphere [arXiv:2411.01572]

Application to superconductivity

Further discussion of superconductivity via AdS/CFT in condensed matter physics (beyond the references above):

On strange metals, high T cT_c-superconductors and AdS/CMT duality:

Application to chiral magnets

  • Yuki Amari, Muneto Nitta, Chiral Magnets from String Theory [arXiv:2307.11113]

Application to quasicrystals

Discussion of asymptotic boundaries of hyperbolic tensor networks as conformal quasicrystals:

Relation to pp-adic AdS/CFT correspondence

Proposed realization of aspects of p-adic AdS/CFT correspondence in solid-state physics:

  • Gregory Bentsen, Tomohiro Hashizume, Anton S. Buyskikh, Emily J. Davis, Andrew J. Daley, Steven Gubser, Monika Schleier-Smith, Treelike interactions and fast scrambling with cold atoms, Phys. Rev. Lett. 123, 130601 (2019) (arXiv:1905.11430)

Topological phases of matter via K-theory

For free-fermion topological insulators

On the classification (now often referred to, somewhat rudimentarily, as the ten-fold way) of free fermion topological phases of matter (condensed matter with gapped Hamiltonians, specifically topological insulators) by twisted equivariant topological K-theory:

Early detailed discussion (ignored by the revival of the idea following Kitaev 2009)

Later precursor discussion phrased in terms of random matrix theory instead of K-theory:

The original proposal making topological K-theory explicit:

  • Alexei Kitaev: Periodic table for topological insulators and superconductors, talk at: L. D. Landau Memorial Conference “Advances in Theoretical Physics”, June 22-26, 2008, in:

    AIP Conference Proceedings 1134 (2009) 22-30 [doi:10.1063/1.3149495, arXiv:0901.2686]

Further details:

The technical part of the argument always essentially boils down (implicitly, never attributed this way before Freed & Moore 2013) to the argument for Karoubi K-theory from:

More on this Clifford algebra-argument explicit in view of topological insulators:

  • Michael Stone, Ching-Kai Chiu, Abhishek Roy, Symmetries, dimensions and topological insulators: the mechanism behind the face of the Bott clock, Journal of Physics A: Mathematical and Theoretical, 44 4 (2010) 045001 [[doi:10.1088/1751-8113/44/4/045001]]

  • Gilles Abramovici, Pavel Kalugin, Clifford modules and symmetries of topological insulators, International Journal of Geometric Methods in Modern PhysicsVol. 09 03 (2012) 1250023 [[arXiv:1101.1054, doi:10.1142/S0219887812500235]]

The proper equivariant K-theory formulation expected to apply also to topological crystalline insulators:

Further discussion:

Review:

Generalization of the K-theory classification of free topological pgases to include interacting topological order:

On T-duality in the K-theory classification of topological phases of matter (related to the Fourier transform between crystals and their Brillouin torus) as expressing the bulk-boundary correspondence:

Review:

Further on the bulk-boundary correspondence:

Discussion via cobordism cohomology:

Relation to the GSO projection:

With application of the external tensor product of vector bundles to describe coupled systems:

For quasicrystals via KK-theory of the noncommutative topology of quasiperiodicity:

  • Jean Bellissard, The Noncommutative Geometry of Aperiodic Solids, in: Geometric and Topological Methods for Quantum Field Theory, pp. 86-156 (2003) (pdf, doi:10.1142/9789812705068_0002)

  • Fonger Ypma, Quasicrystals, C *C^\ast-algebras and K-theory, 2005 (pdf)

  • Ian F. Putnam, Non-commutative methods for the K-theory of C *C^\ast-algebras of aperiodic patterns from cut-and-project systems, Commun. Math. Phys. 294, 703–729 (2010) (pdf, doi:10.1007/s00220-009-0968-0)

  • Hervé Oyono-Oyonoa, Samuel Petite, C *C^\ast-algebras of Penrose hyperbolic tilings, Journal of Geometry and Physics Volume 61, Issue 2, February 2011, Pages 400-424 (doi:10.1016/j.geomphys.2010.09.019)

Holographic

Under AdS/CFT duality in solid state physics the K-theory-classification of topological phases of matter translates to the K-Theory classification of D-brane charge in string theory, allowing a dual description of the topological phases even at strong coupling via AdS/CFT duality:

Relation to Yang-Mills monopoles as Dp/D(p+2)-brane intersections and Yang-Mills instantons as Dp/D(p+4)-brane intersections:

  • Koji Hashimoto, Taro Kimura, Band spectrum is D-brane, Progress of Theoretical and Experimental Physics, Volume 2016, Issue 1 (arXiv:1509.04676)

  • Charlotte Kristjansen, Gordon W. Semenoff, The D3-probe-D7 brane holographic fractional topological insulator, JHEP10 (2016) 079 (arXiv:1604.08548)

Last revised on February 13, 2025 at 04:24:14. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (72 revisions) Cite Print Source