nLab electronic band structure
Context
Solid state physics
-
basics
-
Examples
Contents
Idea
By Bloch-Floquet theory the available energies of electron-excitations in crystals depends smoothly on the momentum/wave number of the excitation, taking values in the Brillouin torus, and otherwise only on a discrete index set labelling the remaining “quantum numbers?” (the electron‘s orbitals?, spin. etc.). Fixing the latter values (and jointly denoting them , say), the given function (or rather its graph) is called the th electronic band (or just th band, for short) of the material.
Often, the values of are closely spaced as varies in certain subsets of its allowed values. For instance if includes the spin of the electrons and if there is a (typically small) spin-orbit coupling and no sizeable external magnetic field, then the energies and differ (only) slightly. In these cases the graphs of these values jointly look approximately like a single but thickened curve (as such shown in the following schematic graphics), which is where the name “band” originates from.
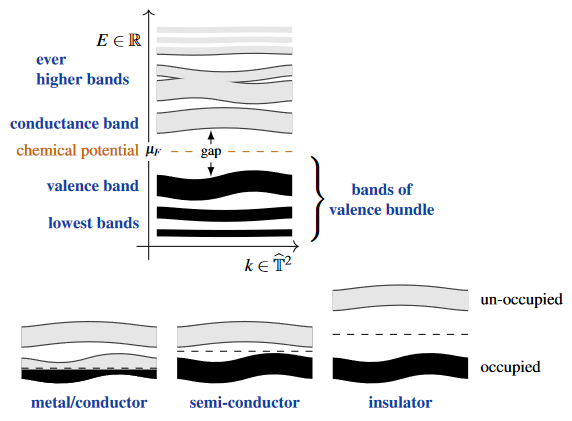
The band geometry around the electron chemical potential of a material controls its electrical conductivity:
 (graphics from SS 22)
(graphics from SS 22)
| metal/conductor | the electron chemical potential is inside the valence band |
| insulator | the electron chemical potential is inside a large gap between (what is then) the valence- and conduction-band |
| semi-conductor | the electron chemical potential is inside a small gap between valence and conduction band |
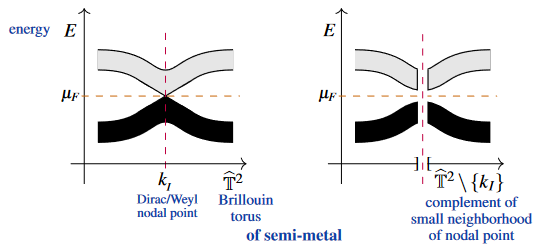
| semi-metal | there is a large gap between valence and conduction band, except over a codimension locus, where the gap closes right at the chemical potential |
 (graphics from SS 22)
(graphics from SS 22)
Related concepts
-
energy band structure is also observed in “metamaterials” such as:
References
General
Textbook accounts:
-
Karlheinz Seeger, Section 2 of: Semiconductor Physics, Advanced texts in physics, Springer (2004) doi:10.1007/978-3-662-09855-4
-
Sheng San Li, Energy Band Theory, in S. S. Li, (ed.): Semiconductor Physical Electronics, Springer (2006) 61-104 doi:10.1007/0-387-37766-2_4
Lecture notes:
- David Tong, Chapter 2 of: Lectures on solid state physics (2017) pdf, webpage
Account with focus on topological phases of matter (topological insulators, semimetals etc.):
-
David Vanderbilt, Berry Phases in Electronic Structure Theory – Electric Polarization, Orbital Magnetization and Topological Insulators, Cambridge University Press (2018) (doi:10.1017/9781316662205)
-
Jérôme Cayssol, Jean-Noël Fuchs, Topological and geometrical aspects of band theory, J. Phys. Mater. 4 (2021) 034007 (arXiv:2012.11941, doi:10.1088/2515-7639/abf0b5)
See also:
- Wikipedia, Electronic band structure
Discussion of bands of metamaterials over hyperbolic spaces by a hyperbolic variant of Bloch's theorem:
-
Joseph Maciejko, Steven Rayan, Hyperbolic band theory, Science Advances 7 36 (2021) [doi:10.1126/sciadv.abe9170]
-
Adil Attar, Igor Boettcher, Selberg trace formula in hyperbolic band theory, Phys. Rev. E 106 034114 (2022) [arXiv:2201.06587, doi:10.1103/PhysRevE.106.034114]
Examples
The electronic band structure of graphene was predicted in
-
Philip Russel Wallace, The Band Theory of Graphite, Phys. Rev. 71 (1947) 622 (doi:10.1103/PhysRev.71.622)
-
Selberg trace formula in hyperbolic band theory Adil Attar, Igor Boettcher
For interacting electrons
-
Yuejin Guo, Jean-Marc Langlois and William A. Goddard, Electronic Structure and Valence-Bond Band Structure of Cuprate Superconducting Materials, New Series, 239 4842 (1988) 896-899 [jstor:1700316]
-
Jingsan Hu, Jianfei Gu, Weiyi Zhang, Bloch’s band structures of a pair of interacting electrons in simple one- and two-dimensional lattices, Physics Letters A 414 (2021) 127634 [doi:10.1016/j.physleta.2021.127634]
Last revised on January 12, 2025 at 12:58:39. See the history of this page for a list of all contributions to it.