nLab gluing function
Redirected from "gluing functions".
Context
Manifolds and cobordisms
manifolds and cobordisms
cobordism theory, Introduction
Definitions
Genera and invariants
Classification
Theorems
Contents
Definition
Definition
(local chart and atlas and gluing function)
Given an -dimensional topological manifold (def. ), then
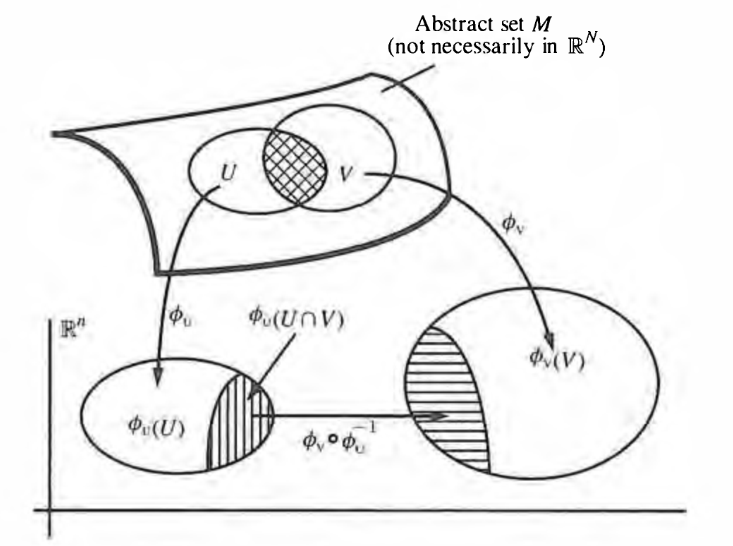
-
an open subset and a homeomorphism is also called a local coordinate chart of .
-
an open cover of by local charts is called an atlas of the topological manifold.
-
denoting for each the intersection of the th chart with the th chart in such an atlas by
then the induced homeomorphism
is called the gluing function or coordinate transformation from chart to chart .
graphics grabbed from Frankel
Related concepts
Last revised on June 28, 2017 at 15:11:32. See the history of this page for a list of all contributions to it.