nLab differentiable manifold
Context
Differential geometry
synthetic differential geometry
Introductions
from point-set topology to differentiable manifolds
geometry of physics: coordinate systems, smooth spaces, manifolds, smooth homotopy types, supergeometry
Differentials
Tangency
The magic algebraic facts
Theorems
Axiomatics
Models
differential equations, variational calculus
Chern-Weil theory, ∞-Chern-Weil theory
Cartan geometry (super, higher)
Manifolds and cobordisms
manifolds and cobordisms
cobordism theory, Introduction
Definitions
Genera and invariants
Classification
Theorems
Contents
Idea
A differentiable manifold is a topological space which is locally homeomorphic to a Euclidean space (a topological manifold) and such that the gluing functions which relate these Euclidean local charts to each other are differentiable functions, for a fixed degree of differentiability. If one considers arbitrary differentiablity then one speaks of smooth manifolds and if one demands analytic gluing functions then one speaks of analytic manifolds. For a general discussion see at manifold.
Accordingly, a differentiable manifold is a space to which the tools of (infinitesimal) analysis may be applied locally. Notably we may ask whether a continuous function between differentiable manifolds is differentiable by computing its derivatives pointwise in any of the Euclidean coordinate charts.
In particular one may consider smooth functions from the real line into any smooth manifold , “smooth curves” in . The equivalence classes of these that have the same first derivative at a given point capture the idea of “infinitsimal smooth paths” through that point in the manifold, called its tangent vectors. All the tangent vectors at one point constitute the tangent space , and the collection of all these tangent spaces yields another differentiable manifold, called the tangent bundle . This happens to be a vector bundle which is associated to a principal bundle, called the frame bundle .
By equipping the tangent bundle or frame bundle of a differentiable manifold with extra properties or extra structure one encodes geometry on the manifold. For example equipping them with orthogonal structure encodes Riemannian geometry on manifolds. More generally one may consider any G-structure on the frame bundle and thereby equip the manifold with the corresponding Cartan geometry, for instance complex geometry, conformal geometry etc.
This way differential and smooth manifolds are the basis for differential geometry. They are the analogs in differential geometry of what schemes are in algebraic geometry. In fact both of these concepts are unified within synthetic differential geometry.
If one relaxes the condition on differentiable manifold from it being locally isomorphic to a Euclidean space to it just admitting local smooth maps from a Euclidean space, then one obtains the more general concept of diffeological spaces or even smooth sets, see at generalized smooth space for more on this. If one generalizes here differentiable functions to simplicial differentiable functions one obtains concepts of derived smooth manifold.
The generalization of differentiable manifolds to higher differential geometry are orbifolds and more generally differentiable stacks. If one combines this with the generalization to smooth sets then one obtains the concept of smooth stacks and eventually smooth infinity-stacks.
Definition
For convenience, we first recall the basic definition of
and of
and then turn to the actual definition of
Topological manifolds
For convenience, we first recall here some background on topological manifolds:
Definition
(topological manifold)
A topological manifold is a topological space which is
If the local Euclidean neighbourhoods are all of dimension for a fixed , then the topological manifold is said to be a -dimensional manifold or -fold. This is usually assumed to be the case.
Remark
(varying terminology)
Often a topological manifold (def. ) is required to be sigma-compact. But by this prop. this is not an extra condition as long as there is a countable set of connected components. Moreover, manifolds with uncountably many connected components are rarely considered in practice.
Definition
(local chart, atlas and gluing function)
Given an -dimensional topological manifold (def. ), then
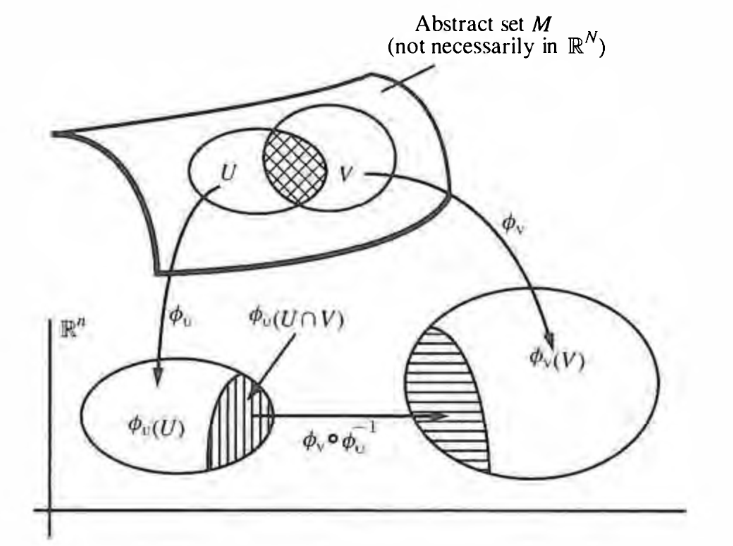
-
an open subset and a homeomorphism is also called a local coordinate chart of .
-
an open cover of by local charts is called an atlas of the topological manifold.
-
denoting for each the intersection of the th chart with the th chart in such an atlas by
then the induced homeomorphism
is called the gluing function from chart to chart .
graphics grabbed from Frankel
Differentiable functions between Cartesian spaces
For convenience we recall the definition of differentiable functions between Euclidean spaces.
Definition
(differentiable functions between Euclidean spaces)
Let and let be an open subset.
Then a function is called differentiable at if there exists a linear map such that the following limit exists as approaches zero “from all directions at once”:
This means that for all there exists an open subset containing such that whenever we have .
We say that is differentiable on a subset of if is differentiable at every , and differentiable if is differentiable on all of . We say that is continuously differentiable if it is differentiable and is a continuous function.
The map is called the derivative or differential of at .
More generally, let and let be an open subset.
Then a function is differentiable if for all the component function
is differentiable in the previous sense
In this case, the derivatives of the assemble into a linear map of the form
If the derivative exists at each , then it defines itself a function
to the space of linear maps from to , which is canonically itself a Euclidean space. We say that is twice continuously differentiable if is continuously differentiable.
Generally then, for the function is called -fold continuously differentiable or of class if the -fold differential exists and is a continuous function.
Finally, if is -fold continuously differentiable for all then it is called a smooth function or of class .
Of the various properties satisfied by differentiation, the following plays a special role in the theory of differentiable manifolds (notably in the discussion of their tangent bundles):
Proposition
(chain rule for differentiable functions between Euclidean spaces)
Let and let
be two differentiable functions (def. ). Then the derivative of their composite is the composite of their derivatives:
hence for all we have
Differentiable manifolds
Definition
(differentiable manifold and smooth manifold)
For then a -fold differentiable manifold or -manifold for short is
-
a topological manifold (def. );
-
an atlas (def. ) all whose gluing functions are times continuously differentiable.
A -fold differentiable function between -fold differentiable manifolds
is
such that
-
for all and then
is a -fold differentiable function between open subsets of Euclidean space.
(Notice that this in in general a non-trivial condition even if and is the identity function. In this case the above exhibits a passage to a different, but equivalent, differentiable atlas.)
If a manifold is differentiable for all , then it is called a smooth manifold. Accordingly a continuous function between differentiable manifolds which is -fold differentiable for all is called a smooth function,
Remark
(category Diff of differentiable manifolds)
In analogy to remark there is a category called Diff (or similar) whose objects are -differentiable manifolds and whose morphisms are -differentiable functions, for given .
The analog of the concept of homeomorphism (def. ) is now this:
Definition
Given smooth manifolds and (def. ), then a smooth function
is called a diffeomorphism, if there is an inverse function
which is also a smooth function (hence if is an isomorphism in the category Diff from remark ).
Here it is important to note that while being a topological manifold is just a property of a topological space, a differentiable manifold carries extra structure encoded in the atlas:
Definition
Let be a topological manifold (def. ) and let
be two atlases (def. ), both making into a smooth manifold (def. ).
Then there is a diffeomorphism (def. ) of the form
precisely if the identity function on the underlying set of constitutes such a diffeomorphism. (Because if is a diffeomorphism, then also is a diffeomorphism.)
That the identity function is a diffeomorphism between equipped with these two atlases means, by definition , that
Notice that the functions on the right may equivalently be written as
showing their analogy to the glueing functions within a single atlas spring.
Hence diffeomorphism induces an equivalence relation on the set of smooth atlases that exist on a given topological manifold . An equivalence class with respect to this equivalence relation is called a smooth structure on .
As Étale Spaces
Differentiable manifolds can be viewed as akin to étale spaces, very much in alignment with the language of algebraic geometry. For smooth manifolds and complex manifolds the requisite atlas conditions can be stated in terms of a particular structure sheaf. More precisely, this definition yields an equivalence of categories between the category of smooth manifolds as in and the category of locally ringed spaces modeled on domains of with a sheaf of germs of smooth functions. The same goes for topological and complex manifolds, where the local models are domains with sheafs of germs of continuous and holomorphic functions respectively. Here we illustrate the differentiable case. For any , we write for the sheaf of germs of functions . That is, is the functor s.t. and . This turns into a ringed space, and any ringed space modeled on one of this kind can be regarded as a differentiable (by which is always meant “real”) manifold. More precisely, given a ringed space , there must an open set and local isomorphism where is a continuous function with sheaf pushfoward . The following property, which holds at the continuous level, is essential.
Lemma
Let be a continuous surjection. Let be a sheaf of -valued functions on (here we let be any ring). Consider an open and define to be i.e. those s.t. the pullback of each by belongs to . Then is a sheaf on .
We can phrase the example of in this language.
Example
(real projective space as a smooth manifold in this étale map sense)
We need only show that the functions which are smooth when composed with the canonical projection form a sheaf on . Denote these . Certainly they form a presheaf, and checking the pullback as in the lemma confirms that they are a sheaf. So far this only confirms that is a real topological manifold. To establish its differentiable structure we take for each chart of the ringed space obtained from restriction and then pushforward, a local isomorphism of locally ringed spaces by construction. Hence is a smooth manifold.
Examples
Example
(Cartesian space as a smooth manifold)
For then the Cartesian space equipped with the atlas consisting of the single chart is a smooth manifold, in particularly a -fold differentiable manifold for every according to def. .
Similarly the open disk becomes a smooth manifold when equipped with the atlas whose single chart is the homeomorphism .
This defines a smooth structure (def. ) on and . Strikingly, precisely for there are other smooth structures on , hence called exotic smooth structures.
Example
(n-spheres as smooth manifolds)
For all , the n-sphere becomes a smooth manfold, with atlas consisting of the two local charts that are given by the inverse functions of the stereographic projection from the two poles of the sphere onto the equatorial hyperplane
By the formulas given in this prop. the induced gluing function is a rational function, and hence a smooth function.
Finally the -sphere is a paracompact Hausdorff topological space. Ways to see this include:
-
is a compact subspace by the Heine-Borel theorem. Compact spaces are evidently also paracompact. Moreover, Euclidean space, like any metric space, is Hausdorff, and subspaces of Hausdorff spaces are Hausdorff;
-
The -sphere has an evident structure of a CW-complex and CW-complexes are paracompact Hausdorff spaces.
Example
(real projective space and complex projective space)
For
-
the real projective space has the structure of a smooth manifold of dimension ;
-
the complex projective space has the structure of a smooth manifold of (real) dimension .
where in both cases the atlas is given by the standard open cover (this def.).
By this prop..
We now discuss some general mechanisms by which new differentiable manifolds arise from given ones:
Example
(product manifold)
Let any be two differentiable manifolds with atlases and . Then their product topological space becomes an differentiable manifold with respect to the atlas
Example
(open subsets of differentiable manifolds are differentiable manifolds)
Let be a -fold differentiable manifold and let be an open subset of the underlying topological space .
Then carries the structure of a -fold differentiable manifold such that the inclusion map is an open embedding of differentiable manifolds.
Proof
Since the underlying topological space of is locally connected (this prop.) it is the disjoint union space of its connected components (this prop.).
Therefore we are reduced to showing the statement for the case that has a single connected component. By this prop this implies that is second-countable topological space.
Now a subspace of a second-countable Hausdorff space is clearly itself second countable and Hausdorff.
Similarly it is immediate that is still locally Euclidean: since is locally Euclidean every point has a Euclidean neighbourhood in and since is open there exists an open ball in that (itself homeomorphic to Euclidean space) which is a Euclidean neighbourhood of contained in .
For the differentiable structure we pick these Euclidean neighbourhoods from the given atlas. Then the gluing functions for the Euclidean charts on are -fold differentiable follows since these are restrictions of the gluing functions for the atlas of .
Example
For , the general linear group is a smooth manifold (as an open subspace of Euclidean space , via example and example ).
The group operations are smooth functions with respect to this smooth manifold structure, and thus is a Lie group.
Related concepts
References
See also the references at smooth manifold.
The vision of the modern notion of manifolds is attributed to:
-
Bernhard Riemann, Über die Hypothesen, welche der Geometrie zu Grunde liegen, Göttingen (1845) [doi:10.1007/978-3-642-35121-1]
Engl. transl: William Clifford: On the hypotheses which underlie geometry, Nature VIII (1873) 183-184 [doi:10.1007/978-3-319-26042-6]
Monographs:
-
Antoni Kosinski, Differential manifolds, Academic Press 1993 (pdf)
-
William M. Boothby, An introduction to differentiable manifolds and Riemannian geometry, Academic Press (1975, 1986), Elsevier (2002) [ISBN:9780121160517, pdf]
-
Theodore Frankel, chapter 1 of: The Geometry of Physics - An Introduction, Cambridge University Press (1997, 2004, 2012)
Lecture notes include
-
Claudio Gorodski, Notes on smooth manifolds, 2013 (pdf)
-
Henrik Schlichtkrull, Differentiable manifolds, 2008 (pdf)
See also
- Wikipedia, Differentiable manifold
Last revised on May 16, 2024 at 15:23:18. See the history of this page for a list of all contributions to it.