nLab surface

Idea

A surface is a space of dimension 2, usually understood to be connected.

In differential topology/differential geometry this means a 2-dimensional (differentiable/smooth) manifold.

In complex analytic geometry this usually means a complex manifold of complex dimension 2 (hence real dimension 4).

Similarly and more generally, in algebraic geometry an algebraic surface is a variety of algebraic dimension 2.

Properties

Classification

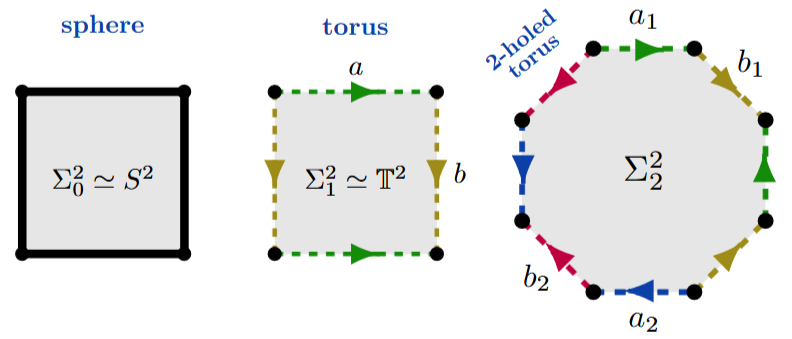
The oriented closed real surfaces are classified, up to isomorphism, by a natural number $g \in \mathbb{N}$ called the genus (intuitively its “number of holes”, in a sense):

genus	oriented surface
$0$	2-sphere $S^2$
$1$	2-torus $\mathbb{T}^2$
$2$	double torus $\Sigma^2_2$

(cf. Kinsey 1991 Thm. 4.14, Gallier & Xu 2013 Thm 6.3, Thm. 4.14)

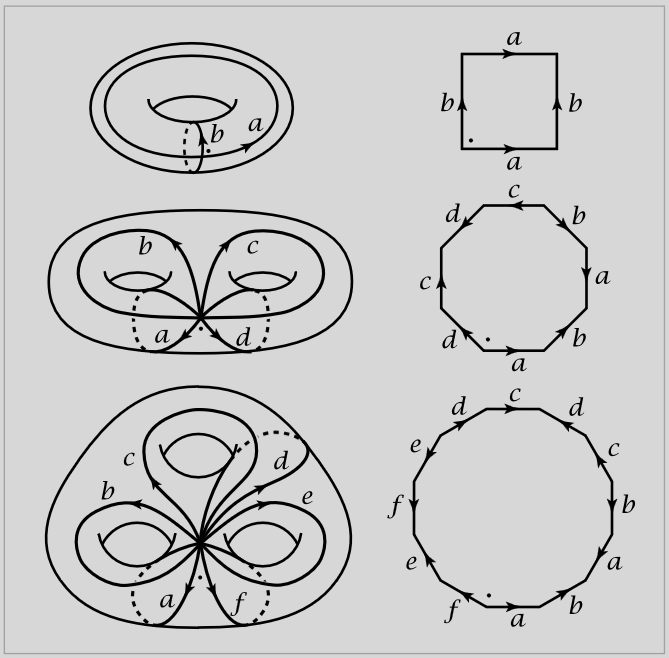
Here the closed oriented surface $\Sigma^2_g$ of genus $g$ may be obtained from the regular $4g$-gon by identifying

• all the boundary vertices with a single point,

and, going clockwise for $k \in \{0, \cdots, g-1\}$,

• the $4k+1$st boundary edge with the reverse of the $4k +3$rd,

• the $4k+2$nd edge with the reverse of the $4k+4$th.

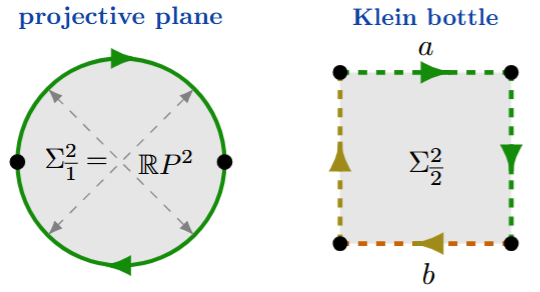
Similarly, the non-orientable closed real surfaces are classified by a positive natural number $h \in \mathbb{N}_{\geq 1}$, also called the (non-orientable) genus or the number of crosscaps

# crosscaps	non-orientable surface
$1$	projective plane $\mathbb{R}P^2$
$2$	Klein bottle $\mathbb{R}P^2 # \mathbb{R}P^2$

Here the non-orientable surface $\Sigma^2_{\overline{g}}$ with $h$ crosscaps may be obtained from the regular $2h$-gon by identifying

• all the boundary vertices with a single point,

and, going clockwise for $k \in \{0, \cdots, h-1\}$,

• the $2k+1$st boundary edge with the $2k + 2$nd.

(This is a conveniently concise but not the most intuitively visualized choice of fundamental polygons – other choices are possible and often discussed, cf. also MO:q/172784.)

Homotopy

The above classification may be restated in algebro-topological terms by saying that (the homotopy type of) the oriented closed genus$=g$ surface has a 2-dimensional CW-complex-structure exhibited by the following pointed cell attachment:

Here $\bigvee_{2g} S^1$ is the wedge sum of $2g$ circles, whose fundamental group is the free group on $2g$ generators $(a_i, b_i)_{i=1}^g$, and the attaching map is a representative in this free group of the composition of group commutators

$$[a_i, b_i] \;\coloneqq\; a_i \cdot b_i \cdot a_i^{-1} \cdot b_i^{-1} \,,$$

as indicated.

Similarly for (the homotopy type of) the non-orientable surface $\Sigma^2_{\overline{h}}$ of crosscap number $h$:

It follows that:

Proposition

The fundamental group of the oriented closed real surface $\Sigma^2_g$ of genus $g \in \mathbb{N}$ (see above) is the quotient group of the free group on $2g$ generators $(a_1, \cdots, a_g, \, b_1, \cdots, b_g)$ by the normal subgroup generated by the group product of the group commutators $[a_i, b_i]$ of the sequence of pairs of generators:

$$\pi_1\big( \Sigma^2_g \big) \;\simeq\; \big\langle a_1, \cdots, a_g ,\, b_1, \cdots, b_g \big\rangle \big/ \Big( \textstyle{\prod_i} [a_i, b_i] \Big) \,.$$

Similarly, the fundamental group of the non-orientable closed real surface $\Sigma^2_{\overline{h}}$ with $h \in \mathbb{N}_{\geq 1}$ crosscaps is the quotient group of the free group on $h$ generators $(a_1, \cdots, a_h)$ by the normal subgroup generated by the group product of the squares $a^2_ \,\coloneqq\, a_i \cdot a_i$ of the sequence of pairs of generators:

$$\pi_1\big( \Sigma^2_{\overline{h}} \big) \;\simeq\; \big\langle a_1, \cdots, a_h \big\rangle \big/ \Big( \textstyle{\prod_i} a_i^2 \Big) \,.$$

(cf. Gallier & Xu 2013 p 100, Actipes 2013 Thm. 6.3).

Examples

• plane

• sphere

• torus

• Klein bottle

Related concepts

• punctured surface

• differential geometry of curves and surfaces

• analog for dimension 1: curve, algebraic curve

• genus of a surface

• area

• moduli space of curves

• complex surface

• surface knot

• hypersurface

• minimal surface

manifolds in low dimension:

• 2-manifolds

• 3-manifolds

• 4-manifolds

• 5-manifolds

• 8-manifolds

References

Monographs:

• L. Christine Kinsey: Topology of Surfaces, Spinger (1991) [doi:10.1007/978-1-4612-0899-0, pdf]

• Richard E. Schwartz: Mostly Surfaces, American Mathematical Society, Student Mathematical Library 60 (2011) [draft: pdf, endmatter:pdf]

• Jean Gallier, Dianna Xu: A Guide to the Classification Theorem for Compact Surfaces, Springer (2013) [doi:10.1007/978-3-642-34364-3, Wikipedia entry]

• Clark Bray, Adrian Butcher, Simon Rubinstein-Salzedo, chapters 2 & 4 of: Algebraic Topology, Springer (2021) [doi:10.1007/978-3-030-70608-1, pdf]

See also:

• Wikipedia: Surface (topology)

• Wikipedia: Genus g surface

• Manifold Atlas, 2-manifolds

• Peter Andrews: The Classification of Surfaces, The American Mathematical Monthly 95 9 (1988) 861-867 [doi:10.2307/2322906, jstor:2322906]

Review and exposition of the classification of surfaces by fundamental polygons:

• E. C. Zeeman: An Introduction to Topology – The Classification theorem for Surfaces [pdf, pdf, pdf]

• Chen Hui George Teo: Classification of Surfaces, REU notes (2011) [pdf, pdf]

• Thomas George: The Classification of Surfaces with Boundary, REU notes (2001) [pdf, pdf]

• Eugene Gorsky: Classification of Surfaces, lecture notes (2021) [pdf]

• Ana da Silva Rodrigues: Classification of Surfaces, BSc thesis, ETH (2023) [pdf, pdf]

See also:

• Wikipedia: Fundamental polygon

Review of the computation of the fundamental group of surfaces:

• Matthew Actipes: On the fundamental group of surfaces, REU notes (2013) [pdf, pdf]

Discussion of de Rham cohomology of surfaces:

• William Fulton, §18 of: Algebraic Topology – A First Course, Graduate Texts in Mathematics 153, Springer (1995) [doi:10.1007/978-1-4612-4180-5]