nLab cobordism

Idea

An (oriented) cobordism $\Sigma$ from an (oriented) smooth manifold $X_{in}$ to an (oriented) smooth manifold $X_{out}$ is a smooth manifold with boundary such that its boundary is the disjoint union

$$\partial \Sigma \simeq X_{in} \coprod X_{out}$$

with induced orientation agreeing with the given one on $X_{in}$ and being the opposite of that of $X_{out}$ (Thom 54, Chapter IV, p. 64). Hence by labelling disjoint components of the boundary of any manifold with boundary $\Sigma$ as either “incoming” or “outgoing”, then $\Sigma$ becomes a cobordism from its incoming to its outgoing boundary components.

(While $X_{in} \coprod X_{out}$ is the boundary of $\Sigma$, conversely $\Sigma$ is the “co-boundary” of $X_{in}\coprod X_{out}$. This is part of the reason for the “co-” in “cobordism”, but sometimes one just says bordism. The difference is more pronounced when distinguishing between bordism homology theory and cobordism cohomology theory.)

With a few technical conditions on the boundary inclusions added, then $(n-1)$-dimensional manifolds with diffeomorphism classes of $n$-dimensional cobordisms between them form a category (a category of cobordisms) whose objects are the manifolds, whose morphisms are the cobordisms, and whose composition operation is the operation of gluing two cobordisms along a common boundary component. Such a category of cobordisms $Bord_n$ of some dimension $n$ is naturally a symmetric monoidal category $Bord_n^{\sqcup}$ with the tensor product being the disjoint union $\sqcup$ of manifolds.

The connected components in this category are called cobordism classes of manifolds. Under cartesian product and disjoint union, these form what is called the cobordism ring in the given dimension. The study of these classes, hence of manifolds “up to cobordisms”, is a central topic in algebraic topology.

A central insight connecting algebraic topology with mathematical physics is that a strong monoidal functor on a category of cobordisms with values in something like the category Vect (with its standard tensor product of modules) may be thought of as a formalized incarnation of what in physics is called a topological quantum field theory

$$Z \colon Bord_n^\sqcup \longrightarrow Vect^\otimes \,.$$

Here one thinks of a cobordism $\Sigma$ as a piece of spacetime (or worldvolume) of dimension $n$, and of the $(n-1)$-dimensional manifolds that this goes between as a piece of space (or brane). A functor $Z$ as above is then thought of as sending each $(n-1)$-dimensional space $X$ to its space of quantum states $Z(X)$ and each spacetime $\Sigma$ between $X_{in}$ and $X_{out}$ to a linear map $Z(\Sigma)\colon Z(X_{in}) \longrightarrow Z(X_{out})$.

From the perspective of mathematics, such a functor is a way to break up diffeomorphism invariants of closed manifolds of dimension $n$ into pieces and being able to reconstruct them from gluing of data associated to manifolds with $(n-1)$-dimensional boundary.

If one considers manifolds with corners, then there is a fairly evident extension of the concept of cobordism that allows refinement of this gluing process to extended cobordisms of any dimension $k$ going between extended cobordisms of dimension $k-1$. Such extended cobordisms of maximal dimension $n$ form a symmetric monoidal (infinity,n)-category called, naturally, the (infinity,n)-category of cobordisms. The cobordism hypothesis asserts that this is a most fundamental object in higher category theory and higher algebra, namely that it is the free symmetric monoidal (infinity,n)-category with duals. The corresponding extended concept of topological quantum field theory is accordingly called extended TQFT or similar.

Properties

Relation to Cohomotopy

The Pontrjagin-Thom isomorphism says that assigning Cohomotopy charge identifies suitable cobordism classes of submanifolds or abstract manifolds with cocycles in unstable Cohomotopy (see here) or stable Cohomotopy.

The following graphics illustrates the Cohomotopy charge map of the pair creation/annihilation cobordism for 0-dimensional submanifolds:

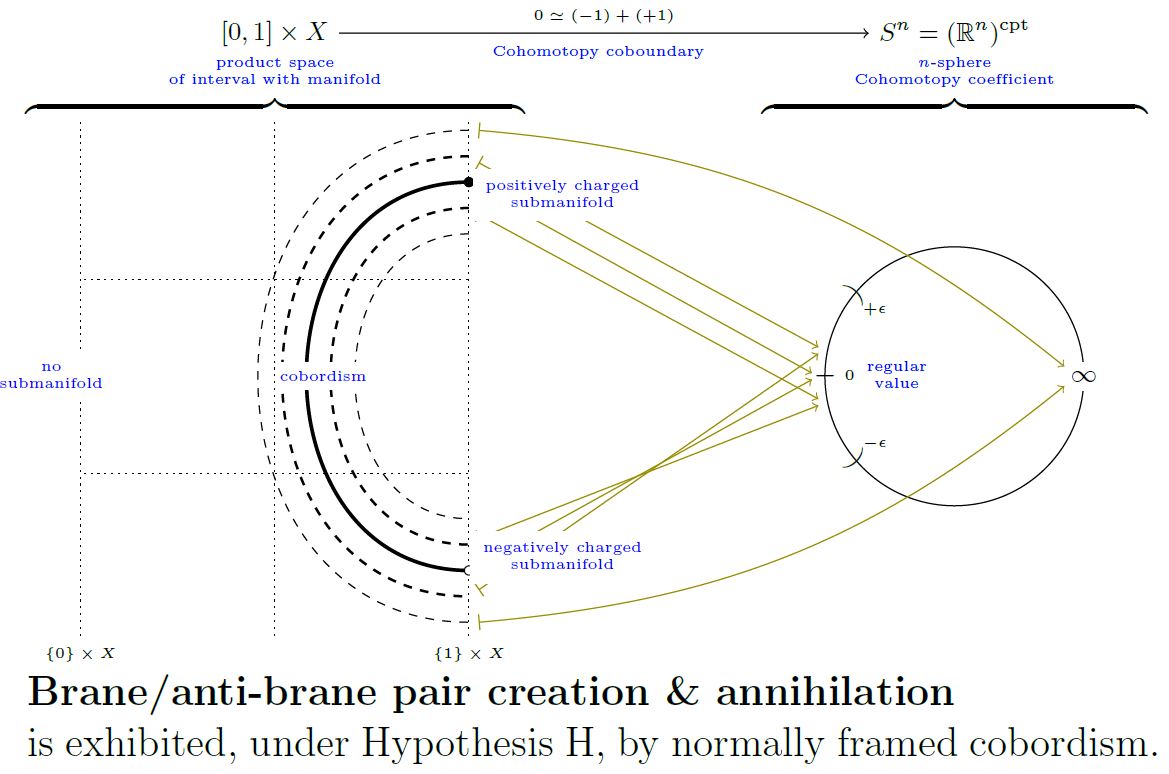
graphics grabbed from SS 19

(See also at Cohomotopy charge – For charged points.)

Related concepts

• handlebody

• h-cobordism

• movie

• cobordism theory

• cobordism group, cobordism ring

• Thom spectrum, Thom's theorem

• cobordism category

• (infinity,n)-category of cobordisms, cobordism hypothesis

• cobordism cohomology theory

• extended cobordism

• B-bordism

• orbifold cobordism

• Lagrangian cobordism

• algebraic cobordism

• Sullivan chord diagram

• link cobordism

• braid cobordism

References

The notion originates with

• René Thom, p. 64 of: Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28, (1954). 17-86 (doi:10.1007/BF02566923, dml:139072, digiz:GDZPPN002056259, pdf)

• Lev Pontrjagin, Section III.6, p. 41 of: Smooth manifolds and their applications in homotopy theory, Trudy Mat. Inst. im Steklov, No 45, Izdat. Akad. Nauk. USSR, Moscow, 1955 (AMS Translation Series 2, Vol. 11, 1959) (doi:10.1142/9789812772107_0001)

(Beware that Pontrjagin still wrote “homology” for “cobordism”, following an earlier tradition that got abandoned.)

An early textbook account:

• Robert Stong, Notes on Cobordism theory, 1968 (toc pdf, publisher page)

Further review:

• Peter Landweber, A survey of bordism and cobordism, Mathematical Proceedings of the Cambridge Philosophical Society 100 2 (1986) 207-223 [doi:10.1017/S0305004100066032]

• Friedrich Hirzebruch, Thomas Berger, Rainer Jung, Section 1.1 of: Manifolds and Modular Forms, Aspects of Mathematics 20, Viehweg (1992), Springer (1994) [doi:10.1007/978-3-663-10726-2, pdf]

• Stanley Kochmann, section 1.5 of Bordism, Stable Homotopy and Adams Spectral Sequences, AMS 1996

• John Francis (notes by Owen Gwilliam), Topology of manifolds, Lecture 2: Cobordism (pdf)

• Manifold Atlas, Bordism

• Wikipedia, Cobordism

For more see at cobordism cohomology theory.

A relation to fixed point spaces:

• Carlos Prieto, Fixed point theory and framed cobordism, Topol. Methods Nonlinear Anal. Volume 21, Number 1 (2003), 155-169. (euclid:tmna/1475266278)