nLab topological manifold
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Manifolds and cobordisms
manifolds and cobordisms
cobordism theory, Introduction
Definitions
Genera and invariants
Classification
Theorems
Contents
Idea
A topological manifold is a topological space (usually required to be Hausdorff and paracompact) which is locally homeomorphic to a Euclidean space equipped with its metric topology.
Often one is interested in extra structure on topological manifolds, that make them for instance into differentiable manifolds or smooth manifolds or analytic manifolds or complex manifolds, etc. See at manifold for more on the general concept.
Topological manifolds form a category TopMfd.
Definition
Locally Euclidean topological spaces
Definition
(locally Euclidean topological space)
A topological space is locally Euclidean if every point has an open neighbourhood which is homeomorphic to the Euclidean space with its metric topology:
The “local” topological properties of Euclidean space are inherited by locally Euclidean spaces:
Proposition
(locally Euclidean spaces are -separated, sober, locally connected, locally compact)
Let be a locally Euclidean space (def. ). Then
-
satisfies the separation axiom;
-
is sober;
-
is locally compact in the sense that every open neighbourhood of a point contains a compact neighbourhood.
Proof
Regarding the first statement:
Let be two distinct points in the locally Euclidean space. We need to show that there is an open neighbourhood around that does not contain .
By definition, there is a Euclidean open neighbourhood around . If does not contain , then it already is an open neighbourhood as required. If does contain , then are equivalently two distinct points in . But Euclidean space, as every metric space, is , and hence we may find an open neighbourhood not containing . By the nature of the subspace topology, is an open neighbourhood as required.
Regarding the second statement:
We need to show that the map
that sends points to the topological closure of their singleton sets is a bijection with the set of irreducible closed subsets. By the first statement above the map is injective (via this lemma). Hence it remains to see that every irreducible closed subset is the topological closure of a singleton. We will show something stronger: every irreducible closed subset is a singleton.
So let be an open proper subset such that if there are two open subsets with then or . By this prop. we need to show that there exists a point such that it its complement.
Now since is a proper subset, and since the locally Euclidean space is covered by Euclidean neighbourhoods, there exists a Euclidean neighbourhood such that is a proper subset. In fact this still satisfies the condition that for then implies or . Accordingly, by that prop. it follows that is an irreducible closed subset of Euclidean space. Sine metric spaces are sober topological space as well as -separated, this means that there exists such that .
In conclusion this means that the restriction of an irreducible closed subset in to any Euclidean chart is either empty or a singleton set. This means that the irreducible closed subset must be a disjoint union of singletons that are separated by Euclidean neighbourhoods. But by irreducibiliy, this union has to consist of just one point.
Regarding the third statement:
Let be a point and a neighbourhood. We need to find a connected open neighbourhood .
By local Euclideanness, there is also a Euclidean neighboruhood . Since is a homeomorphism, and since is open, also is open. This means that there exists an open ball . This is open and connected, and hence so is its homeomorphic image . This is a connected open neighbourhood of as required.
Regarding the fourth statement:
Let be a point and let be an open neighbourhood. We need to find a compact neighbourhood .
By assumption there exists a Euclidean open neighbourhood . By definition of the subspace topology the intersection is still open as a subspace of and hence is an open neighbourhood of .
Since Euclidean spaces are locally compact, there exists a compact neighbourhood (for instance a sufficiently small closed ball around , which is compact by the Heine-Borel theorem). Now since continuous images of compact spaces are compact, it follows that also is a compact neighbourhood.
But the “global” topological properties of Euclidean space are not generally inherited by locally Euclidean spaces. This sounds obvious, but notice that also Hausdorff-ness is a “global property”:
Remark
(locally Euclidean spaces are not necessarily )
It might superficially seem that every locally Euclidean space (def. ) is necessarily a Hausdorff topological space, since Euclidean space, like any metric space, is Hausdorff, and since by definition the neighbourhood of every point in a locally Euclidean spaces looks like Euclidean space.
But this is not so, Hausdorffness is a “non-local condition”.
Example
counter-example: (non-Hausdorff locally Euclidean spaces)
An example of a locally Euclidean space (def. ) which is a non-Hausdorff topological space, is the line with two origins.
Lemma
(connected locally Euclidean spaces are path-connected)
A locally Euclidean space which is connected is also path-connected.
Proof
Fix any . Write for the subset of all those points of which are connected to by a path, hence
Observe now that both as well as its complement are open subsets:
To see this it is sufficient to find for every point an open neighbourhood such that , and similarly for the complement.
Now by assumption every point has a Euclidean neighbourhood . Since Euclidean space is path connected, there is for every a path connecting with , i.e. with and . Accordingly the composite path
connects with . Hence .
Similarly, if is not connected to by a path, then also all point in cannot be connected to by a path, for if they were, then the analogous concatenation of paths would give a path from to , contrary to the assumption.
It follows that
is a decomposition of as the disjoint union of two open subsets. By the assumption that is connected, exactly one of these open subsets is empty. Since is not empty, as it contains , it follows that its compement is empty, hence that , hence that is path connected.
Proposition
(equivalence of regularity conditions for Hausdorff locally Euclidean spaces)
Let be a locally Euclidean space (def. ) which is Hausdorff.
Then the following are equivalent:
-
is sigma-compact,
-
is second-countable,
-
is paracompact and has a countable set of connected components,
Proof
Generally, observe that is locally compact: By prop. every locally Euclidean space is locally compact in the sense that every point has a neighbourhood base of compact neighbourhoods, and since is assumed to be Hausdorff, this implies all the other variants of definition of local compactness, by this prop..
1) 2)
Let be sigma-compact. We show that then is second-countable:
By sigma-compactness there exists a countable set of compact subspaces. By being locally Euclidean, each admits an open cover by restrictions of Euclidean spaces. By their compactness, each of these has a subcover with a finite set. Since countable unions of countable sets are countable, we have obtained a countable cover by Euclidean spaces . Now Euclidean space itself is second countable (by this example), hence admits a countable set of base open sets. As a result the union is a base of opens for . But this is a countable union of countable sets, and since countable unions of countable sets are countable we have obtained a countable base for the topology of . This means that is second-countable.
1) 3)
Let be sigma-compact. We show that then is paracompact with a countable set of connected components:
Since locally compact and sigma-compact spaces are paracompact, it follows that is paracompact. By local connectivity (prop. ) is the disjoint union space of its connected components (this prop.). Since, by the previous statement, is also second-countable it cannot have an uncountable set of connected components.
2) 1) Let be second-countable, we need to show that it is sigma-compact.
This follows since locally compact and second-countable spaces are sigma-compact.
3) 1)
Now let be paracompact with countably many connected components. We show that is sigma-compact.
Since is locally compact, there exists a cover by compact subspaces. By paracompactness there is a locally finite refinement of this cover. Since paracompact Hausdorff spaces are normal, the shrinking lemma applies to this refinement and yields a locally finite open cover
as well as a locally finite cover by closed subsets. Since this is a refinement of the orignal cover, all the are contained in one of the compact subspaces . Since subsets are closed in a closed subspace precisely if they are closed in the ambient space, the are also closed as subsets of the . Since closed subsets of compact spaces are compact it follows that the are themselves compact and hence form a locally finite cover by compact subspaces.
Now fix any .
We claim that for every there is a finite sequence of indices with the property that .
To see this, first observe that it is sufficient to show sigma-compactness for the case that is connected. From this the general statement follows since countable unions of countable sets are countable. Hence assume that is connected. It follows from lemma that is path-connected.
Hence for any and there is a path connecting with . Since the closed interval is compact and since continuous images of compact spaces are compact, it follows that there is a finite subset of the that covers the image of this path. This proves the claim.
It follows that there is a function
which sends each to the minimum natural number as above.
We claim now that for all the preimage of under this function is a finite set. Since countable unions of countable sets are countable this implies that is a countable cover of by compact subspaces, hence that is sigma-compact.
We prove this last claim by induction. It is true for by construction. Assume it is true for some , hence that is a finite set. Since finite unions of compact subspaces are again compact (this prop.) it follows that
is compact. By local finiteness of the , every point has an open neighbourhood that intersects only a finite set of the . By compactness of , the cover has a finite subcover. In conclusion this implies that only a finite number of the intersect .
Now by definition is a subset of those which intersect , and hence itself finite.
Topological manifold
Definition
A topological manifold is a topological space which is
-
locally Euclidean (def. ),
If the local Euclidean neighbourhoods are all of dimension for a fixed , then the topological manifold is said to be a -dimensional manifold or -fold. This is usually assumed to be the case.
Remark
(varying terminology)
Often a topological manifold (def. ) is required to be sigma-compact. But by prop. this is not an extra condition as long as there is a countable set of connected components.
Differentiable manifolds
Definition
(local chart and atlas and gluing function)
Given an -dimensional topological manifold (def. ), then
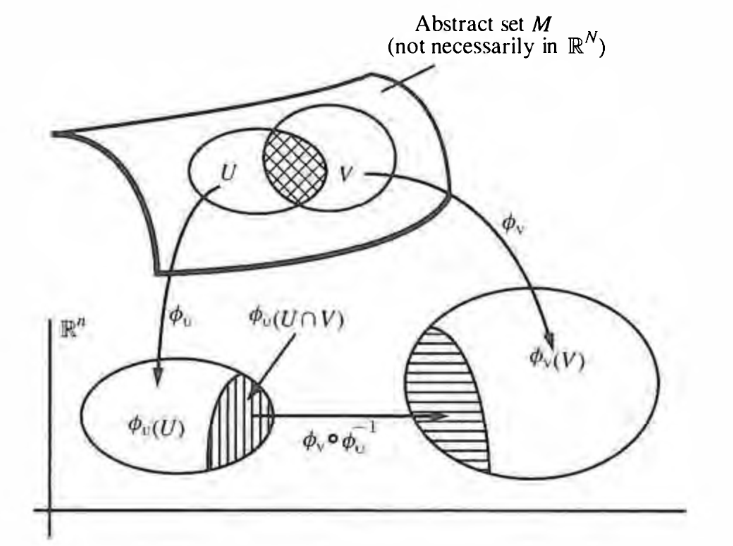
-
an open subset and a homeomorphism is also called a local coordinate chart of .
-
an open cover of by local charts is called an atlas of the topological manifold.
-
denoting for each the intersection of the th chart with the th chart in such an atlas by
then the induced homeomorphism
is called the gluing function from chart to chart .
graphics grabbed from Frankel
Definition
(differentiable and smooth manifolds)
For then a -fold differentiable manifold is
-
a topological manifold (def. );
-
an atlas (def. ) all whose gluing functions are times continuously differentiable.
A -fold differentiable function between -fold differentiable manifolds
is
such that
-
for all and then
is a -fold differentiable function between open subsets of Euclidean space.
Notice that this in in general a non-trivial condition even if and is the identity function. In this case the above exhibits a passage to a different, but equivalent, differentiable atlas.
Properties
Proposition
Let be a -fold differentiable manifold and let be an open subset of the underlying topological space .
Then carries the structure of a -fold differentiable manifold such that the inclusion map is an open embedding of differentiable manifolds.
Proof
Since the underlying topological space of is locally connected (this prop.) it is the disjoint union space of its connected components (this prop.).
Therefore we are reduced to showing the statement for the case that has a single connected component. By this prop this implies that is second-countable topological space.
Now a subspace of a second-countable Hausdorff space is clearly itself second countable and Hausdorff.
Similarly it is immediate that is still locally Euclidean: since is locally Euclidean every point has a Euclidean neighbourhood in and since is open there exists an open ball in that (itself homeomorphic to Euclidean space) which is a Euclidean neighbourhood of contained in .
For the differentiable structure we pick these Euclidean neighbourhoods from the given atlas. Then the gluing functions for the Euclidean charts on are -fold differentiable follows since these are restrictions of the gluing functions for the atlas of .
Examples
See the examples at differentiable manifold.
Related concepts
References
Historical articles:
-
Hellmuth Kneser, Die Topologie der Mannigfaltigkeiten, Jahresbericht der Deutschen Mathematiker-Vereinigung (1926), Volume: 34, page 1-13 (eudml:145701)
-
J. W. Cannon, The recognition problem: What is a topological manifold?, Bull. Amer. Math. Soc. 84 (1978), 832-866 (doi:10.1090/S0002-9904-1978-14527-3)
Textbook accounts:
- John M. Lee, Introduction to topological manifolds, Graduate Texts in Mathematics 202, Springer (2000) [ISBN: 0-387-98759-2, 0-387-95026-5]
Second edition: Springer (2011) [ISBN:978-1-4419-7939-1, doi:10.1007/978-1-4419-7940-7, errata pdf]
See also:
- Wikipedia, Topological manifold
Last revised on June 11, 2024 at 17:08:56. See the history of this page for a list of all contributions to it.