Schreiber Some Quantum States of M-Branes under Hypothesis H

A talk that I have given:

---

• Urs Schreiber on joint work with Hisham Sati:

  
  

  Some Quantum States of M-Branes under Hypothesis H

  
  

  talk at

  Centre for Research in String Theory

  Queen Mary University of London

  Dec 9, 2021

  
  

  download:

  • slides pdf

  • recording (passcode: %E3LRN=@)

---

From HSS18, p. 7

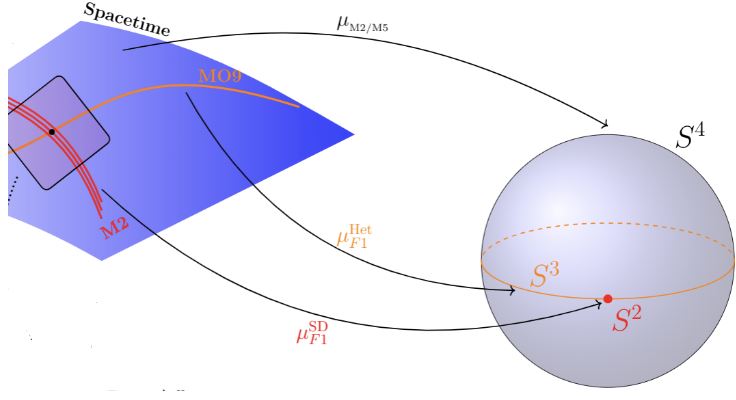
Abstract: Following a proposal by H. Sati, we have recently stated a hypothesis about the mathematical home of the quantum charges in M-theory. This “Hypothesis H” refines the traditional proposal for quantization of D-brane charge from K-theory to the non-abelian cohomology theory known as 4-Cohomotopy, whose classifying space is the 4-sphere.

Besides its motivation from homotopy-theoretic re-analysis of 11d supergravity and of the old brane scan, Hypothesis H is currently justified by its rigorous implication of a list of long-conjectured M-theoretic consistency conditions on C-field flux and M-brane charges – such as shifted C-field flux quantization, dual Page charge quantization and M2/M5-brane tadpole cancellation.

From SS19, p. 15

But if Hypothesis H is a correct assumption about the nature of M-theory, this suggests that quantum states of full M-theory should be reflected in the positive cohomology of the moduli space of Cohomotopy cocycles, much like quantum states of non-perturbative Chern-Simons theory are in the Dolbeault cohomology of moduli spaces of (flat) connections.

From SS19, p. 50

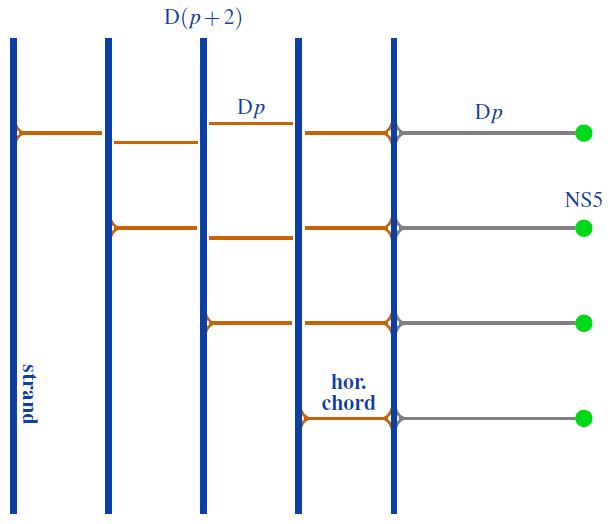
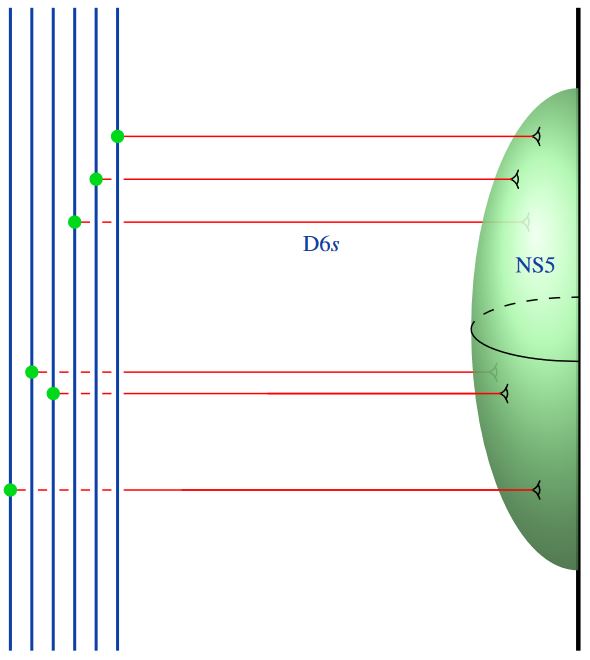
In this talk I discuss how, in the topological sector of $D6 \perp D8$-brane intersections, such quantum states according to Hypothesis H are identified with weight systems on horizontal chord diagrams, and how these do reflect a range of phenomena expected from the traditional approaches to understanding these brane intersections, such as non-abelian DBI-theory, the BMN matrix model, Rozansky-Witten theory and Hanany-Witten theory.

Specifically, we have proven that the fundamental $\mathfrak{gl}_2(\mathbb{C})$-weight system satisfies the positivity condition that characterizes physical (i.e. non-ghost) quantum states. Under the above identification, this quantum state corresponds to an elementary fuzzy funnel configuration and to the elementary transverse M5-brane state in the BMN matrix model – both as expected for D6/D8-brane intersections.

From SS19, p. 46

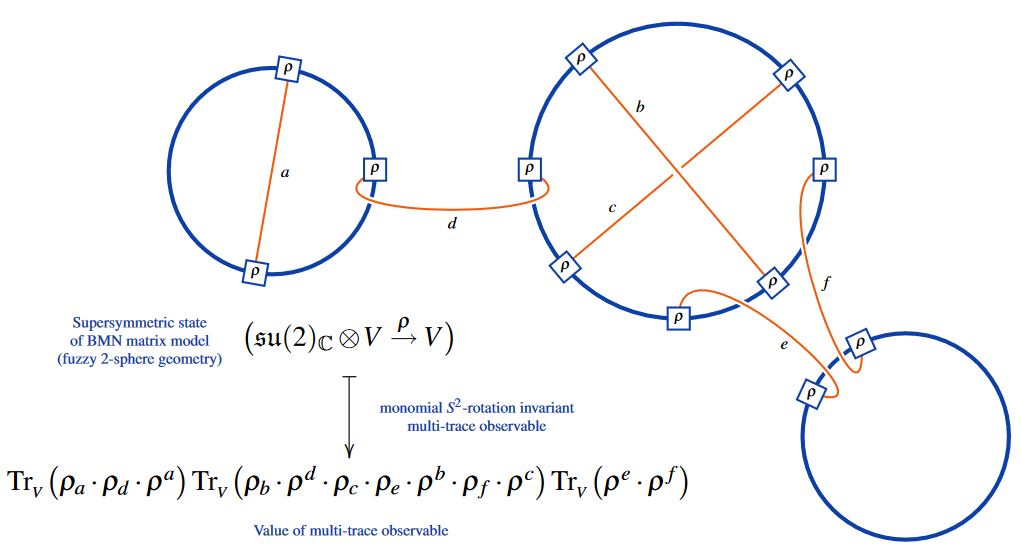
Besides possible implications for the elusive formulation of M-theory, this result may provide a unifying explanation for the plethora of unexpected appearances that chord diagrams are recently making in fundamental high energy physics, notably in discussion of holographic entanglement entropy.

Based on:

• Hisham Sati, Urs Schreiber:

  Differential Cohomotopy implies intersecting brane observables

  arXiv:1912.10425

• David Corfield, Hisham Sati, Urs Schreiber:

  Fundamental weight systems are quantum states

  arXiv:2105.02871

Related talks:

• Proper Orbifold Cohomotopy for M-Theory

  talk at String and M-Theory: The New Geometry of the 21st Century – II

  via NUS Singapore, 2021

• Microscopic Brane Physics from Cohomotopy

  talk at M-Theory and Mathematics

  NYU Abu Dhabi, 2020

For more see:

• Hypothesis H.

---