nLab M-Theory and Mathematics

This page compiles material related to:

A conference series on M-theory and mathematics.

These workshops bring together experts on mathematical aspects of M-theory, a candidate non-perturbative “theory of everything”, with implications to string theory, quantum field theory and condensed matter theory, and interactions with geometry and algebraic topology.

M-Theory and Mathematics 2024

on January 15 - 17, 2024

at CQTS @ New York University, Abu Dhabi

• program: pdf

• abstracts: pdf

• poster: pdf

Speakers:

• Luigi Alfonsi

• Chris Blair

• Mario Garcia-Fernandez

• Grigorios Giotopoulos

• Fei Han

• Yang-Hui He

• Olaf Hohm

• Chris Hull

• Neil Lambert

• Emanuel Malek

• Ruben Minasian

• Christian Saemann

• Hisham Sati

• Urs Schreiber

• Carlos Shahbazi

• Eric Sharpe

Alfonsi$\,$Giotop. Malek Saemann Minasian Lambert Hull Schreiber He Sati X Han Tan Singh Shahbazi Myers Hohm

Talks:

• 15 Jan 2024

  Neil Lambert:

  Non-Relativistic M2-Branes and AdS/CFT

  slides: pdf

  video: kt

  cf.: arXiv:2401.14955

  We discuss a peculiar limit of M2-branes that leads to a non-relativistic Chern-Simons-matter theory with an infinite dimensional spacetime symmetry group and whose dynamics leads to quantum mechanics on a Hitchin moduli space. We also discuss the corresponding limit in the gravitational dual which is described by an eleven-dimensional Membrane-Newton-Cartan theory about a background with an $AdS_2$ factor.

• 15 Jan 2024

  Carlos Shahbazi:

  The Differential Geometry and Topology of Four- Dimensional Universal Supergravity

  slides: pdf

  video: kt

  cf.: arXiv:2101.07236

  Using the cohomology of the appropriate locally constant sheaf I will explain how to implement the Dirac-Schwinger-Zwanziger integrality condition on four-dimensional classical ungauged supergravity and how to interpret it geometrically in order to obtain its duality-covariant, gauge-theoretic, differential-geometric global model. Using this construction, I will prove that four-dimensional bosonic ungauged supergravity is completely determined by a choice of polarized Siegel bundle defined over the total space of a vertically Riemannian submersion equipped with a complete Ehresmann connection, showing that its gauge sector reduces to a polarized self-duality condition for connections on the underlying polarized Siegel bundle. Furthermore, I will explore the continuous and arithmetic U-duality groups of the theory, characterizing them through short exact sequences and realizing the latter through the automorphism group of the underlying Siegel bundle acting on its adjoint bundle. This elucidates the geometric origin of U-duality and justifies the miraculous existence of U-dualities by describing them as a gauge transformation of the appropriately defined principal bundle.

• 15 Jan 2024

  Mario Garcia-Fernandez:

  Gauge Theory for String Algebroids

  video: kt

  cf.: arXiv:arXiv:2004.11399

  In this talk I will explain a moment map construction for string algebroids, a special type of Courant algebroids which arise as Atiyah algebroids of higher principal bundles. The zero locus of our moment map is given by the solutions of the Calabi system, a coupled system of equations which provides a unifying framework for the classical Calabi problem and the Hull-Strominger system in heterotic string theory. Our main results are concerned with the geometry of the moduli space of solutions, and assume a technical condition which is fulfilled in examples. We prove that the moduli space carries a pseudo-Kähler metric with Kähler potential given by the dilaton functional, a topological formula for the metric, and an infinitesimal Donaldson-Uhlenbeck-Yau type theorem. Based on joint work with Rubio and Tipler in arXiv:arXiv:2004.11399 (to appear in JDG) and ongoing joint work with Álvarez-Cónsul and Tellez.

• 15 Jan 2024

  Grigorios Giotopoulos:

  Towards Non-Perturbative Lagrangian Field Theory via the Topos of Smooth Sets

  video: kt

  cf.: arXiv:2312.16301

  Any notion of non-pertubative (pre)-quantization of classical field theories, as in particular expected in M-theoretic contexts, presupposes a convenient category within which non-pertubative classical field theory may be rigorously formalised. In this talk, I will describe smooth sets as a category of generalized smooth spaces, completely determined by “how they may be smoothly probed by finite dimensional manifolds”. Formally, this is the “topos of sheaves over the site of Cartesian spaces”. I will then explain how the variational algorithm of (bosonic) classical field theory and the space of on-shell fields naturally take place in smooth sets, along with many more field theoretic concepts. Time permitting, I will indicate how the setting naturally generalizes to include the description of infinitesimal (pertubative) structure, fermionic fields, and (gauge) fields with internal symmetries.

• 15 Jan 2024

  Luigi Alfonsi:

  Towards Non-Perturbative BV-Theory via Derived Geometry and the Puzzle of Quantisation

  video: kt

  cf.: arXiv:arXiv:2307.15106

  In this talk I will introduce and discuss a global geometric framework which allows one to encode a natural non-perturbative generalisation of classical Batalin–Vilkovisky(BV-)theory. First, I will set the stage by briefly describing the current state of the art of perturbative BV-theory. Then, I will introduce a concrete model of derived differential geometry, whose geometric objects are formal derived smooth stacks (i.e. stacks on formal derived smooth manifolds), and which is obtained by applying Töen-Vezzosi’s homotopical algebraic geometry to the theory of derived manifolds of Spivak and Carchedi-Steffens. I will explain how derived differential geometry is able to capture non-perturbative classical BV-theory by means of examples: scalar field theory and Yang-Mills theory. Finally, I will discuss some open questions, most importantly on quantisation and on applications to global aspects of M-theory.

• 15 Jan 2024

  Eric Sharpe:

  Decomposition of 2D Pure Yang-Mills and the Gross- Taylor String Theory

  slides: pdf

  video: kt

  cf.: arXiv:2307.08729

  In this talk, we will attempt to reconcile two different results on two-dimensional pure Yang-Mills theory. Specifically, we will discuss how the fact that 2d pure Yang-Mills is equivalent to a disjoint union of theories, is related to the Gross-Taylor description of 2d pure Yang-Mills as the target-space field theory of a string theory. The Gross-Taylor picture can be understood by first rewriting the Yang-Mills partition function (in a large $N$ limit) as a sum of correlation functions in Dijkgraaf-Witten theories for the symmetric group $S_n$, and then interpreting those Dijkgraaf-Witten correlation functions in terms of branched covers, which leads to the string theory description. We first observe that the decomposition of the pure Yang-Mills aligns perfectly with the decomposition of $S_n$ Dijkgraaf-Witten theory, and then discuss decomposition and the branched covers interpretation. We encounter two puzzles, and to solve them, propose that the Gross-Taylor string theory has a higher-form symmetry.

• 16 Jan 2024

  Ruben Minasian:

  Constraining and Un-constraining Supergravities

  slides: pdf

  video: kt

  I will review various aspects and somewhat surprising consequences of cancellation of (different types of) anomalies in supergravity theories in eight and six dimensions. I will also discuss appearance and importance of exotic (singular, non-spin, non-orientable) backgrounds.

• 16 Jan 2024

  Emanuel Malek:

  Kaluza-Klein Spectrometry for String Theory Compactifications

  slides: pdf

  video: kt

  cf.: arXiv:2212.01135

  I will present a powerful new method that for the first time allows us to compute the Kaluza-Klein spectrum of a large class of string theory compactifications, including those arising in maximal gauged supergravities and beyond. This includes geometries with little to no remaining (super-)symmetries, completely inaccessible by previous methods. I will show how these insights can be used to holographically compute the anomalous dimensions of protected and unprotected operators in strongly-coupled CFTs, as well as to study global properties of their conformal manifolds. I will also show how the method can be used to determine the perturbative stability of non supersymmetric AdS vacua. We will see the importance of higher Kaluza-Klein modes to the physics of string compactifications, e.g. in realising the compactness of moduli spaces, restoring supersymmetry that is lost in a consistent truncation, and in destabilising vacua that appear to stable in lower-dimensional supergravities.

• 16 Jan 2024

  Fei Han:

  Cubic Forms, Anomaly Cancellation and Modularity

  video: kt

  cf.: arXiv:2005.02344

  Freed and Hopkins developed an algebraic theory of cubic forms, which is an analogy to the theory of quadratic forms in topology. They are motivated by the Witten-Freed-Hopkins anomaly cancellation formula in M-theory, which equals a cubic form arising from an $E_8$ bundle over a 12 dimensional spin manifold to the indices of twisted Dirac operators on the manifold. In this talk, we will first review the Witten-Freed-Hopkins anomaly cancellation formula and the algebraic theory of cubic forms, and then show that the cubic forms as well as the anomaly cancellation formula can be naturally derived from modular forms that we construct inspired by the Witten genus and the basic representation of affine $\mathfrak{e}_8$. Following this approach, we obtain new cubic forms and anomaly cancellation formulas on non-spin manifolds and thus provide a unified way to obtain anomaly cancellation formulas of this type. This is based on our joint work with Prof. Ruizhi Huang, Prof. Kefeng Liu and Prof. Weiping Zhang.

• 16 Jan 2024

  Meng-Chwan Tan:

  Topological-Holomorphic $\mathcal{N}=4$ Gauge Theory: From Langlands Duality of Holomorphic Invariants to Mirror Symmetry of Quasi-Topological Strings

  slides: pdf

  video: kt

  cf.: arXiv:2305.15965

  We perform a topological-holomorphic twist of $\mathcal{N}=4$ supersymmetric gauge theory on a four-manifold of the form $M^4 = \Sigma_1 \times \Sigma_2$, and unravel the mathematical implications of its physics. In particular, we consider the cohomology of different linear combinations of the resulting scalar supercharges under S-duality, whence we would be able to derive novel topological and holomorphic invariants of $M^4$ and their Langlands duals. As the twisted theory can be topological along $\Sigma_1$ such that we can dimensionally reduce it to 2d, via the effective sigma-model on $\mathbb{C}_2$, we can also relate these 4d invariants and their Langlands duals to the mirror symmetry of Higgs bundles and that of quasi-topological strings described by the sheaf of chiral differential operators.

• 16 Jan 2024

  Olaf Hohm:

  Double Copy, Double Field Theory & Homotopy Algebras

  video: kt

  The double copy denotes a technology to relate the scattering amplitudes of Yang-Mills theory to those of gravity. While enormously successful at the level of scattering amplitudes, until recently there was no first-principle understanding of how to derive such relations. Such an understanding would be needed in order to describe, for instance, a double copy of classical solutions. I present an approach based on homotopy algebras such as L-infinity algebras that allows one to provide such a first-principle derivation, at least to some finite order in perturbation theory. To this end I review how to formulate Yang-Mills theory as an L-infinity algebra, how to “strip off” color to obtain a different kind of homotopy algebra and, finally, how to combine two copies of these exotic algebras to obtain the L-infinity algebra of gravity in the form of double field theory.

• 16 Jan 2024

  Christian Saemann:

  Atiyah Algebroids for Higher and Groupoid Gauge Theories

  slides: pdf

  video: kt

  We present an Atiyah algebroid picture for higher and groupoid gauge theories. Common to both is the fact that straightforward definitions of curvatures are only suitable for partially flat cases. Instead, one has to adjust the underlying cocycle relations, leading to new curvatures and gauge transformations. The Atiyah algebroid picture I sketch provides a good idea about the origin of adjustments and why they are required even in the relative conventional case of groupoid gauge theories.

• 17 Jan 2024

  Chris Hull:

  Self-Dual $p$-Form Gauge Fields and the Topology of the Graviton

  slides: pdf

  video: kt

  cf.: arXiv:2307.04748

  Sen’s action for a $p$-form gauge field with self-dual field strength coupled to a spacetime metric involves an explicit Minkowski metric and the presence of this raises questions as to whether the action is coordinate independent and whether it can be used on a general spacetime manifold. A natural generalisation of Sen’s action is presented in which the Minkowski metric is replaced by a second metric on spacetime. The theory is covariant and can be formulated on any spacetime. The theory describes a physical sector, consisting of the chiral $p$-form gauge field coupled to the dynamical metric $g$, plus a shadow sector consisting of a second chiral $p$-form and the second metric. The resulting theory is covariant and can be formulated on any spacetime. A spacetime with two metrics has some interesting geometry and some of this is explored here and used in the construction of the interactions. The action has two diffeomorphism-like symmetries, one acting only on the physical sector and one acting only on the shadow sector, with the spacetime diffeomorphism symmetry arising as the diagonal subgroup.

• 17 Jan 2024

  Yang-Hui He:

  The AI Mathematician

  video: kt

  We summarize how AI can approach mathematics in three ways: theorem-proving, conjecture formulation, and language processing. Inspired by initial experiments in geometry and string theory, we present a number of recent experiments on how various standard machine-learning algorithms can help with pattern detection across disciplines ranging from algebraic geometry to representation theory, to combinatorics, and to number theory.

• 17 Jan 2024 (talk canceled last minute and postponed to 31 Jan)

  Chris Blair:

  Geometry and Dualities of Decoupling Limits in String Theory and M-Theory

  cf.: arXiv:2311.10564

  Our understanding of M-theory is based on a duality web connecting different limits of the theory. I’ll discuss the extension of this duality web to a wide variety of decoupling limits related by duality to the null reduction of M-theory (and hence to the proposal that M-theory can be described by Matrix theory). From a modern perspective, these limits involve non-relativistic geometries, leading to new variants of supergravity in 11- and 10-dimensions. I’ll discuss how to systematically explore these corners of M-theory, following the roadmap of arxiv.org/abs/2311.10564.

• 17 Jan 2024

  Hisham Sati:

  M-Theory and Hypothesis H

  video: kt

  I will survey the (co)homotopical perspective on the fields and branes in M-theory, showcasing several recent developments. This talk highlights the classical/prequantum aspects, while the talk by Urs Schreiber will highlight the quantum aspects.

• 17 Jan 2024

  Urs Schreiber:

  Introduction to Quantum Hypothesis H

  video: kt

  A famous hypothesis in string theory says that the RR-fields in 10d supergravity are subject to “flux quantization” in topological K-cohomology theory. From a modernized point of view of rational homotopy theory, analogous reasoning applies to the C-field in 11d supergravity and suggests that its flux should be quantized in the “unstable CoHomotopy” cohomology theory of Borsuk, Pontrjagin and Spanier. I’ll survey this “Hypothesis H” with focus on its implications for quantum observables on intersecting branes. This is joint work with Hisham Sati. Notes are available at: ncatlab.org/schreiber/show/Introduction+to+Hypothesis+H.

M-Theory and Mathematics 2023

• on: January 12-15, 2023

  at: CQTS @ New York University, Abu Dhabi

  see: event webpage

$\phantom{-----}$ (logo adapted from JMP 62 (2021) 042301)

Speakers:

• Luigi Alfonsi

• Meer Ashwinkumar

• Ibrahima Bah

• David Berman

• Michael Duff (had to cancel last minute)

• Fei Han

• Yang-Hui He

• Chris Hull

• Branislav Jurčo

• Neil Lambert

• Alessio Marrani

• Varghese Mathai

• Christian Saemann

• Hisham Sati

• Ashoke Sen

• Urs Schreiber

• Eric Sharpe

• Richard Szabo

• Meng-Chwan Tan (had to cancel last minute)

• Dimitrios Tsimpis

• Alexander Voronov

Valera, Jurčo, Berman, Alfonsi, Han, Schreiber, Mathai, Saemann, Sati, Voronov, Lambert, Bah, Tsimpis, Hull, Marrani, He, Singh, Giotopoulos, Szabo

Titles, Abstracts, and Slides for M-Theory & Math 2023 (in chronological order of talks delivered):

• Ashoke Sen:

  D-instanton amplitudes in string theory

  slides: pdf

  video: YT

  cf. arXiv:2204.02981, arXiv:2207.07138

  D-instantons give non-perturbative contribution to string amplitudes. While the world-sheet theory of open and closed strings gives a systematic procedure for computing these amplitudes, the analysis runs into infrared divergences that do not have any known cure within the world-sheet formalism. We describe how string field theory cures these divergences and gives an unambiguous procedure for computing D-instanton correction to string amplitudes.

• Neil Lambert:

  A non-Lorentzian View of the M5-brane

  slides: pdf

  video: YT

  cf.: arXiv:2011.06968, arXiv:2212.07717

  In this talk we will discuss a path-integral formulation of the M5-brane (2,0) theory based upon a Lagrangian without Lorentz invariance but a novel $SU(1,3)$ spacetime symmetry. This provides a UV complete five-dimensional field theoretic description that we will argue admits a six-dimensional Lorentz invariance at strong coupling.

• Dimitrios Tsimpis:

  Universal accelerating cosmologies from 10d supergravity

  slides: pdf

  video: YT

  cf.: arXiv:2210.10813

  4d Friedmann-Lemaître-Robertson-Walker cosmologies are obtained from time-dependent compactifications of Type IIA 10d supergravity on various classes of 6d manifolds. These cosmologies are universal in that they do not depend on the detailed features of the compactification manifold, but only on the properties which are common to all the manifolds belonging to that class. Once the equations of motion are rewritten as an appropriate dynamical system, the existence of solutions featuring a phase of accelerated expansion is made manifest. Some of the resulting cosmologies exhibit eternal or semi-eternal acceleration, whereas others allow for a parametric control on the number of $\mathrm{e}$-foldings. Moreover, we find several smooth accelerating cosmologies without Big Bang singularities: the universe is contracting in the cosmological past ($T \lt 0$), expanding in the future ($T \gt 0$), while in the vicinity of $T = 0$ it becomes de Sitter in hyperbolic slicing. We also obtain several cosmologies featuring an infinite number of cycles of alternating periods of accelerated and decelerated expansions.

• Varghese Mathai:

  T-duality for loop spaces, or equivalently for the 1D sigma model

  slides: pdf

  video: YT

  cf.: arXiv:1405.1320

  We define exotic twisted $S^1$-equivariant cohomology for the loop space $\mathcal{L}Z$ of a smooth manifold $Z$ via the invariant differential forms on $\mathcal{L}Z$ with coefficients in the (typically non-flat) holonomy line bundle of a gerbe, with differential given by an equivariantly flat superconnection. We introduce the twisted Bismut-Chern character form, a loop space refinement of the twisted Chern character form, which represent classes in the completed periodic exotic twisted $S^1$-equivariant cohomology of $\mathcal{L}Z$. We establish a localisation theorem for the completed periodic exotic twisted $S^1$-equivariant cohomology for loop spaces and apply it to establish T-duality in a background flux in type II String Theory from a loop space perspective. Finally we reinterpret these results as T-duality for the 1D sigma model.

• Fei Han:

  Graded T-duality with H-flux for 2d sigma models

  slides: pdf

  cf.: arXiv:2207.03134

  T-duality in string theory can be realised as a transformation acting on the worldsheet fields in the two-dimensional nonlinear sigma model. Bouwknegt-Evslin-Mathai established the T-duality in a background flux for the first time upon compactifying spacetime in one direction to a principal circle by constructing the T-dual maps transforming the twisted cohomology of the dual spacetimes. In this talk, we will describe our recent work on how to promote the T-duality maps of Bouwknegt-Evslin-Mathai in two aspects. More precisely, we will introduce (1) graded T-duality, concerning the graded T-duality maps of all levels of twistings; (2) the 2-dimensional sigma model picture, concerning the double loop space of spacetimes. This represents our joint work with Mathai.

• Christian Saemann:

  Geometric and Non-Geometric T-duality with Higher Bundles

  slides: pdf

  video: YT

  cf.: arXiv:2204.01783

  I will introduce the notion of adjusted curvatures for higher principal bundles. These will allow me to differentially refine the description of topological T-duality by Nikolaus and Waldorf in terms of principal 2-bundles, leading to a description of full T-duality. I also discuss interesting generalizations that seem to capture the non-geometric cases.

• David Berman:

  Exact Renormalisation Group and statistical Inference

  slides: pdf

  video: YT

  cf.: arXiv:2212.11379

  The exact renormalisation group is used to describe the process of statistical inference in the Bayesian sense.

• Yang-Hui He:

  Machine-Learning Mathematical Structures

  slides: pdf

  video: YT

  cf.: arXiv:2101.06317

  We present a number of recent experiments on how various standard machine-learning algorithms can help with pattern detection across disciplines ranging from string theory, to algebraic geometry, to representation theory, to combinatorics, and to number theory.

  We speculate on whether there is an inherent hierarchy of “difficulty” in mathematics reflected by data. At the heart of the programme is the question how does AI help with mathematical discovery.

• Eric Sharpe:

  An introduction to decomposition

  slides: pdf

  video: YT

  cf.: arXiv:2204.09117

  In this talk I will review work on ‘decomposition’, a property of 2d theories with 1-form symmetries and, more generally, d-dim’l theories with $(d-1)$-form symmetries. Decomposition is the observation that such quantum field theories are equivalent to (‘decompose into’) disjoint unions of other QFTs, known in this context as “universes”.

  Examples include two-dimensional gauge theories and orbifolds with matter invariant under a subgroup of the gauge group. Decomposition explains and relates several physical properties of these theories – for example, restrictions on allowed instantons arise as a “multiverse interference effect” between contributions from constituent universes.

  First worked out in 2006 as part of efforts to understand string propagation on stacks, decomposition has been the driver of a number of developments since. I will walk through general aspects of 2d gauge theories that exhibit decomposition, dive into specifics in orbifold examples, and as time permits, discuss recent work in progress.

• Richard Szabo:

  D-branes and doubled geometry

  slides: pdf

  video: YT

  cf.: arXiv:1910.09997

  We formulate the open string version of the Born sigma-model and describe its conformal boundary conditions. This leads to a general characterisation of D-branes in doubled geometry as maximally isotropic sub-bundles on a para-Hermitian manifold. The reduction of D-branes to a physical spacetime is obtained by describing them as Dirac structures. We also introduce a para-complex counterpart of the generalised complex branes of generalised geometry.

• Chris Hull:

  Charges and Duality in Gravity

  slides: pdf

  video: YT

  cf. arXiv:2209.11716 and refs here

  on exotic $\mathcal{N} = (4,0)$ D=6 supergravity

• Branislav Jurčo:

  Correspondences of Quantum $L_\infty$ Algebras (BV-theories)

  video: YT

  cf.: arXiv:1912.06695, arXiv:2002.11168

  The quantum odd symplectic "category" is constructed from the odd symplectic “category” via an enhancement of Lagrangian relations (correspondences) by half-densities. We extend this approach to the (finite-dimensional) setting of the Batalin-Vilkovisky quantum field theories (quantum L-infinity algebras). We discuss the effective observables of perturbative quantum field theory and the homological perturbation lemma from this point of view.

• Meer Ashwinkumar:

  Matrix Quantization of Classical Nambu Brackets and Super $p$-Branes

  video: YT

  cf.: arXiv:2103.06666

  We will present an explicit matrix algebra quantization of the algebra of volume-preserving diffeomorphisms of the $n$-torus. That is, we approximate the corresponding classical Nambu brackets using $\mathfrak{sl}\big(N^{\lceil n/2\rceil}, \mathbb{C}\big)$-matrices equipped with the finite bracket given by the completely anti-symmetrized matrix product, such that the classical brackets are retrieved in the $N \to \infty$ limit. We then apply this approximation to the super 4-brane in 9 dimensions and give a regularized action in analogy with the matrix quantization of the supermembrane. This action exhibits a reduced gauge symmetry that we discuss from the viewpoint of $L_\infty$-algebras in a slight generalization to the construction of Lie 2-algebras from Bagger-Lambert 3-algebras.

• Ibrahima Bah:

  Non-invertible symmetry, holography and branes

  video: YT

  cf.: arXiv:2208.07373

  In this talk I will discuss some general methods for realizing topological symmetry generators in holography. In particular I will present a specific realization of non-invertible symmetry generators and their fusion rules in holographic duals of $SU(N)/\mathbb{Z}_N$ SYM. This will be both from a bottom-up perspective from an effective theory in $AdS_5$, and from a top-down perspective in terms of D-branes in $AdS_5$ backgrounds.

• Hisham Sati:

  M-theory and matter via Twisted Equivariant Differential (TED) K-theory

  video: YT

  cf.: arXiv:2206.13563

  Various flavors of K-theory play an important role in geometric/topological perspectives on string theory. Ultimately, the twisted equivariant differential (TED) version of K-theory would be what is needed to describe fields and branes in the most general backgrounds. However, this theory has not been constructed yet, but major progress has been made in that direction requiring highly nontrivial machinery. I will describe the main conceptual points here. I will also explain how TED K-theory enters naturally into condensed matter (topological phases) and highlight analogies with high energy physics. All of this embeds in M-theory via Hypothesis H, both from physical and mathematical perspectives.

• Urs Schreiber:

  Topological Quantum Gates from M-Theory

  notes: pdf

  video: YT

  cf.: arXiv:2203.11838

  The promising idea that strongly coupled quantum systems such as (confined QCD or) topologically ordered quantum materials are usefully modeled as worldvolume dynamics on intersecting branes in string theory has been suffering from the latter’s lack of non-perturbative formulation (M-theory), necessary in the realistic regime of small numbers of individual branes (i.e. beyond the usual holographic large-$N$ approximation). In this talk I will briefly review our “Hypothesis H” that brane charge in M-theory is quantized in a twisted equivariant non-abelian generalized cohomology theory called Cohomotopy, where M-brane quantum states are identified inside the twisted equivariant cohomology of the Cohomotopy moduli stack. Then I explain our recent derivation, from this assumption, of anyonic topological order in ground states of M5-brane intersections; and I close with an outlook on how this describes topological quantum logic gates via braiding of defect branes.

• Alexander Voronov:

  The $E_k$ symmetry of dimensional reductions of M-theory

  video: YT

  cf.: arXiv:2111.14810, arXiv:2212.13968

  Hisham Sati and I, on the way to revealing the mystery of 2001 Mysterious Duality of Iqbal, Neitzke, and Vafa, generalized hypothesis H and presented a universal target for each dimensional reduction of M-theory. Each of these targets has the dynamics of supergravity embedded into its structure. The target for $(11-k)$-dimensional M-theory also has an action of the Lie algebra of type $E_k$, responsible for symmetries of $(11-k)$-dim supergravity along with its equations of motion in any spacetime.

• Alessio Marrani:

  Exceptional super Yang-Mills in $27 + 3$ and worldvolume M-theory

  slides: pdf

  video: YT

  cf.: arXiv:1906.10709

  Some time ago, Bars and Sezgin proposed a super Yang-Mills theory in $D=s+t=11+3$ space-time dimensions, with an electric 3-brane that generalizes the 2-brane of M-theory. More recently, Rios, Chester and the speaker found an infinite family of “exceptional” super Yang-Mills theories in $D=s+t=(8n+3)+3$. A particularly interesting case occurs for $n=3$, namely in signature $D=27+3$, in which the superalgebra is centrally extended by an electric 11-brane and its 15-brane magnetic dual. The worldvolume symmetry of the 11-brane has signature $D=11+3$ and can reproduce super Yang-Mills theory in D=$11+3$. Upon reduction to $D=26+2$, the 11-brane reduces to a 10-brane with $10+2$ worldvolume signature. A single time projection gives a $10+1$ worldvolume signature, and it can serve as a model for $D=10+1$ M-theory as a reduction from the $D=26+1$ signature of the bosonic M-theory of Horowitz and Susskind; this is further confirmed by the reduction of chiral $(1,0)$, $D=11+3$ superalgebra to the $\mathcal{N}=1$ superalgebra in $D=10+1$, as found by Rudychev, Sezgin and Sundell some time ago. Extending previous results of Dijkgraaf, Verlinde and Verlinde, I will also put forward the realization of spinors as total cohomologies of (the largest spatially extended) branes which centrally extend the $(1,0)$ superalgebra underlying the corresponding “exceptional” super Yang-Mills theory. Moreover, by making use of an “anomalous” Dynkin embedding, I will present further evidence about Ramond‘s and Sati’s argument that M-theory has hidden Cayley plane fibers.

• Luigi Alfonsi:

  Derived $n$-plectic geometry: towards non-perturbative BV-BFV quantisation and M-theory

  cf.: arXiv:2307.15106

  slides: pdf

  video: YT

  In this talk I will propose the notion of derived $n$-plectic geometry and show that a classical BV-BFV theory can be globally reformulated in this framework.

  A derived $n$-plectic structure is a derived and categorified generalisation of a symplectic structure, where the usual closed 2-form is replaced by a shifted closed $(n+1)$-form on a derived space. I will argue that derived $n$-plectic geometry is to classical BV-BFV theory as ordinary $n$-plectic geometry is to ordinary Lagrangian field theory. I will also discuss the rich homotopy-algebraic structure of observables of a derived $n$-plectic space. Finally, I will point at promising applications of this formalism to non-perturbative quantisation of BV-BFV theories and to global aspects of M-theory.

---

M-Theory and Mathematics 2020

• on: January 27-30, 2020

• at: Research Institute of New York University, Abu Dhabi

• see: event webpage

• and: mtheorymath.org

• Program

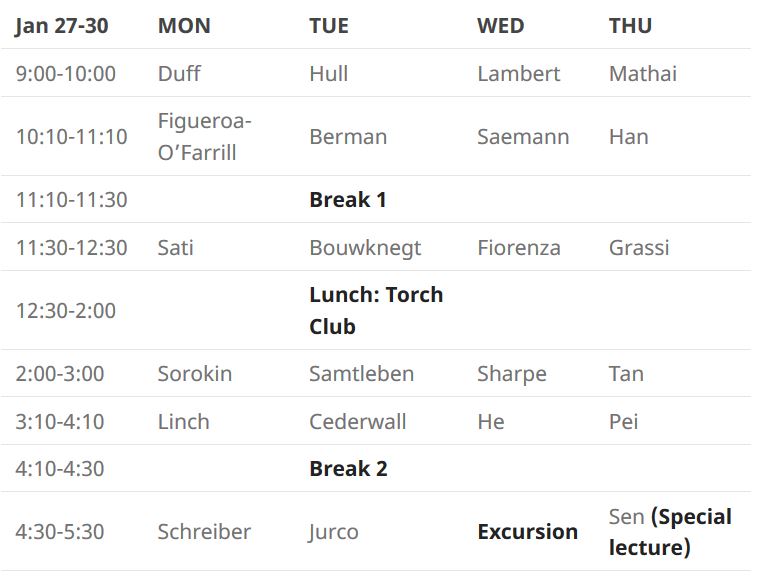
Confirmed speakers:

• David Berman

• Bianca Cerchiai

• Martin Cederwall

• Michael Duff

• José Figueroa-O’Farrill

• Domenico Fiorenza

• Pietro Grassi

• Fei Han

• Yang-Hui He

• Chris Hull

• Branislav Jurčo

• Neil Lambert

• William Linch III

• Varghese Mathai

• Du Pei

• Christian Saemann

• Henning Samtleben

• Hisham Sati

• Urs Schreiber

• Ashoke Sen

• Eric Sharpe

• Dmitri Sorokin

• Meng-Chwan Tan

Abstracts, Slides and Talk notes:

• Michael Duff:

  Perspectives on M-Theory

  video: YT

• José Figueroa-O’Farrill

  Lie superalgebra deformations and d=11 supergravity backgrounds

  slides: pdf

  video: YT

  To every (supersymmetric) background of d=11 supergravity there is associated a filtered Lie superalgebra. For ($\gt 1/2$)-BPS backgrounds, this Lie superalgebra determines the background up to local isometry. I will then report on an algebraic reformulation of this classification problem. This is joint work with Andrea Santi.

• William Linch III

  Off-shell Supersymmetry and the M-theory Effective Action

  video: YT

  cf.: arXiv:2101.11671

• Hisham Sati,

  M-theory and cohomotopy

  slides: pdf

  Cohomotopy theory has recently emerged as the proper generalized cohomology theory to describe the fields in M-theory. It is hoped that viewing M-theory from a mathematical perspective will shed the light on the nature of the theory and will allow for progress. I will survey this area, illustrating how cohomotopy captures the nature of the C-field and its dual as well as of the M-branes, allows for cancellation of various anomalies, and provides a firm grounding for further study of M-theory. This is joint work Urs Schreiber and Domenico Fiorenza.

• Urs Schreiber:

  Microscopic Brane Physics from Cohomotopy

  slides: pdf

  video: YT

  As reviewed in H. Sati‘s talk, assuming that the C-field is charge-quantized in the generalized cohomology theory called J-twisted Cohomotopy (“Hypothesis H”) implies a list of M-theoretic anomaly cancellation conditions, such as shifted C-field flux quantization, DMW anomaly cancellation and C-field tadpole cancellation on 8-manifolds. In this talk I review the further geometric refinement of the cohomology theory to equivariant Cohomotoy theory and to differential Cohomotopy theory. Now we find that Hypothesis H implies also the Witten mechanism of multiple M5-branes on MO5-orientifolds in heterotic M-theory on ADE-orbifolds, hence RR-field tadpole cancellation in type I' string theory; as well as a multitude of effects associated with Dp/D(p+2)-brane intersections: Chan-Paton factors, BMN matrix model fuzzy funnel states and BLG 3-algebras, the Hanany-Witten rules, AdS3-gravity observables, supersymmetric indices of Coulomb branches as well as gauge/gravity duality between all these. This suggests that Hypothesis H is a correct assumption about the elusive mathematical fomulation of M-theory.

This is joint work with H. Sati (arxiv:1909.12277, arxiv:1912.10425).

• Chris Hull:

  Dualities, K3, Exotic Branes and Orientifolds

  video: YT

  cf.: arXiv:1907.04040

• Henning Samtleben:

  Exceptional Field Theories and AdS Compactifications

  video: YT

• Bianca Cerchiai

  Supergravity in a pencil

  slides: pdf slides

  video: YT

  cf.: arXiv:1910.03508

  In the spirit of the gauge-gravity correspondence, we derive a 2+1 dimensional model with “unconventional” supersymmetry at the boundary of a 4-dimensional Anti de Sitter $N$-extended supergravity, which in the case $N=2$ reproduces the AVZ model [P.D. Alvarez, M. Valenzuela, J. Zanelli, JHEP 1204 (2012) 058, arXiv:1109.3944]. The extended supersymmetry of the boundary model is instrumental to describe the electronic properties of graphene, in particular at the two Dirac points. The two valleys correspond to the two independent sectors of the $OSp(p\vert 2)\times OSp(q\vert 2)$ boundary model in the $p=q$ case, which are related by a parity transformation. The Semenoff and the Haldane masses entering the corresponding Dirac equations for the graphene pseudoparticles are identified with supergravity torsion parameters.

• Neil Lambert,

  Lagrangians with $(2,0)$ Supersymmetry

  slides: pdf

  video: YT

  cf.: arXiv:1908.10752

  We will discuss free and interacting six-dimensional actions which admit $(2,0)$ supersymmetry including their application to abelian and non-abelian M5-branes.

• Christian Saemann:

  Towards an M5-Brane Model: Progress Report

  video: YT

  cf.: arXiL1712.06623, arXiv:1908.08086, arXivL2012.09253

• Domenico Fiorenza:

  Twisted Cohomotopy implies level quantization of the 6d WZ term of the M5-brane

  slides: pdf

  video: YT

  cf.: arXiv:1906.07417

  The 6d Wess-Zumino term in the action functional for the M5-brane is anomalous as traditionally defined. What has been missing is a condition implying a higher analogue of level quantization familiar from the 2d Wess-Zumino term. We prove that such an anomaly cancellation condition is implied by the hypothesis that the C-field is charge-quantized in twisted Cohomotopy theory. The proof follows by a twisted/parametrized generalization of the Hopf invariant, after identifying the 6d Wess-Zumino term with a twisted homotopy Whitehead integral formula, which we establish. Joint work with Hisham Sati and Urs Schreiber, arXiv:1906.07417.

• David Berman:

  Strings, Branes, and Boltzmann machines

  video: YT

• Yang-Hui He:

  Universes as Bigdata

  slides: pdf

  video: YT

  We review how historically the problem of string phenomenology lead theoretical physics first to algebraic/differential geometry, and then to computational geometry, and now to data science and AI. With the concrete playground of the Calabi-Yau landscape, accumulated by the collaboration of physicists, mathematicians and computer scientists over the last 4 decades, we show how the latest techniques in machine-learning can help explore problems of physical and mathematical interest.

• Mathai Varghese:

  T-Duality, loop spaces and Witten gerbe modules

  video: YT

  cf.: arXiv:2001.00322

• Dmitri Sorokin:

  What do SYM domain walls look like?

  video: TY

  cf.: arXiv:2004.11232

• Ashoke Sen:

  Gravitational waves from soft theorem

  video: YT

  cf.: arXiv:1912.06413

  on the soft graviton theorem

Related events

• Higher Structures in M-Theory 2018

category: reference