Schreiber thesis Braunack-Mayer

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Authors |

A PhD thesis that I have been advising:

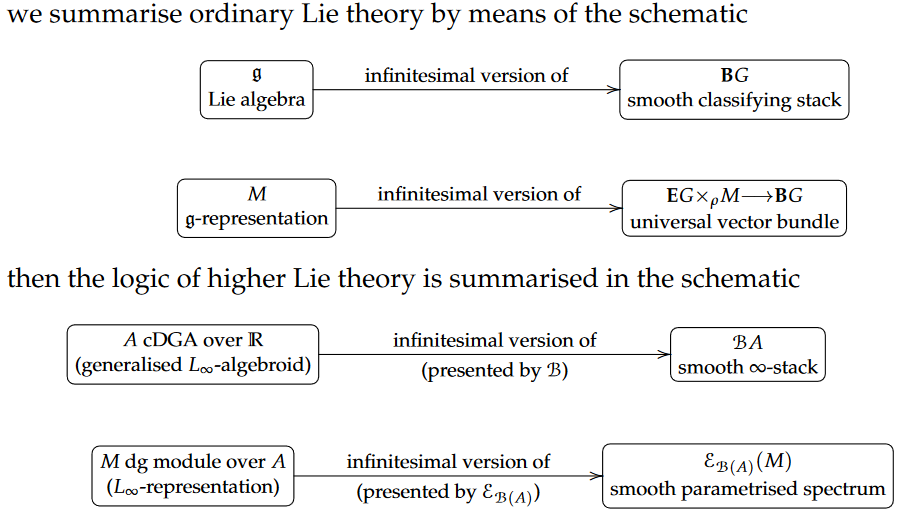
establishing the foundations of rational parameterized stable homotopy theory as well as its Lie integration to smooth parameterized spectra (twisted differential cohomology theories).

Abstract:

This thesis is a study of various aspects of parametrised stable homotopy theory, its rationalisation and its application to twisted differential cohomology. We construct simplicial model categories of parametrised spectra over a fixed base space and relate these to one another via base change adjunctions. We construct model categories for the global homotopy theory of parametrised spectra that have good formal properties, and apply these models to establish a framework for studying twisted differential cohomology via sheaves of parametrised spectra.

Building from Quillen’s rational homotopy theory, we show that the torsion free information of a spectrum parametrised by a 1-connected space is completely encoded by algebraic data. Working over 1-connected base spaces, the rational homotopy theory of parametrised spectra is naturally identified with the homotopy theories of unbounded dg Lie representations and of unbounded dg comodules. We also discuss a dual picture based on Sullivan’s approach to rational homotopy theory, which gives a more direct relationship between parametrised spectra and dg-modules over dg algebras. This dual picture provides a way ofalgebraically presenting twisted cohomology theories and characterises a full subcategory of finitely-presented objects in the rational homotopy category of parametrised spectra in terms of perfect dg modules.

Finally, we conclude by applying our rational homotopy theory results to twisted differential cohomology. We show that that the path method of higher Lie integration is one half of a smooth Sullivan–de Rham adjunction relating smooth ∞-stacks to algebra. Stabilising this adjunction gives a means by which dg modules over real dg algebras produce twisted differential cohomology, an important mechanism by which we can pass from infinitesimal/rational approximations to true homotopy theory. This thesis lays down firm mathematical foundations for future explorations of the role of twisted differential cohomology in quantum field theory and M-theory.

Followup articles

\,

\,

\,

Last revised on November 1, 2019 at 07:38:08. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (16 revisions) Print Source