nLab G₂/SU(3) is the 6-sphere
Context
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Geometry
higher geometry / derived geometry
Ingredients
Concepts
-
geometric little (∞,1)-toposes
-
geometric big (∞,1)-toposes
Constructions
Examples
-
derived smooth geometry
Theorems
Contents
Statement
The coset space of the exceptional Lie group G₂ by its special unitary subgroup SU(3) is diffeomorphic to the 6-sphere:
Related concepts
coset space-structures on n-spheres:
| standard: | |
|---|---|
| this Prop. | |
| this Prop. | |
| this Prop. | |
| exceptional: | |
| Spin(7)/G₂ is the 7-sphere | |
| since Spin(6) SU(4) | |
| since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere | |
| G₂/SU(3) is the 6-sphere | |
| Spin(9)/Spin(7) is the 15-sphere |
see also Spin(8)-subgroups and reductions
homotopy fibers of homotopy pullbacks of classifying spaces:
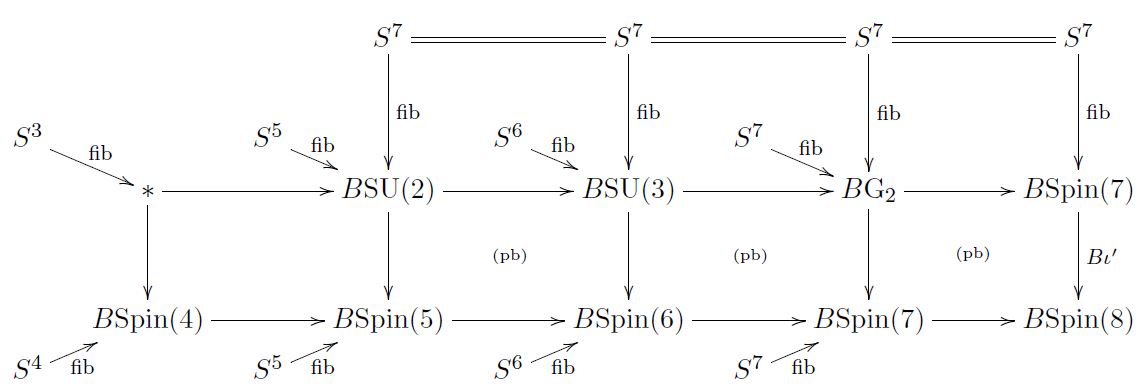
(from FSS 19, 3.4)
References
According to Gray-Green 70, p. 2 the statement is originally due to
- Deane Montgomery, Hans Samelson, Transformation Groups of Spheres, Annals of Mathematics Second Series, Vol. 44, No. 3 (Jul., 1943), pp. 454-470 (jstor:1968975)
According to ABF 17 the statement is originally due to to
- T. Fukami, S. Ishihara, Almost Hermitian structure on , Tohoku Math J. 7 (1955), 151–156 (doi:10.2748/tmj/1178245052)
Review:
-
Alfred Gray, Paul S. Green, p. 2 of Sphere transitive structures and the triality automorphism, Pacific J. Math. Volume 34, Number 1 (1970), 83-96 (euclid:1102976640)
-
Robert Bryant, Section 1.3 of Manifolds with -Holonomy, lecture notes, 1998 (web)
-
Robert Bryant, Section 2.3 of Some remarks on -structures, Proceedings of 12th Gokova Geometry-Topology Conference, 2005 (pdf)
-
Simon Salamon, p. 6 of A tour of exceptional geometry, Milanj. math.72 (2002)1-0 (web)
-
A. J. MacFarlane, The sphere viewed as a -coset space, International Journal of Modern Physics A Vol. 17, No. 19, pp. 2595-2613 (2002) (doi:10.1142/S0217751X02010650)
-
A. Gyenge, Section 4.2 of On the topology of the exceptional Lie group , 2011 (pdf)
-
Ilka Agricola, Aleksandra Borówka, Thomas Friedrich: and the geometry of nearly Kähler 6-manifolds, Differential Geometry and its Applications 57 (2018) 75-86 [arXiv:1707.08591, doi:10.1016/j.difgeo.2017.10.007]
Last revised on June 6, 2025 at 13:39:35. See the history of this page for a list of all contributions to it.