nLab Spin(5)
Context
Group Theory
- group, ∞-group
- group object, group object in an (∞,1)-category
- abelian group, spectrum
- super abelian group
- group action, ∞-action
- representation, ∞-representation
- progroup
- homogeneous space
Classical groups
Finite groups
Group schemes
Topological groups
Lie groups
Super-Lie groups
Higher groups
Cohomology and Extensions
Related concepts
Spin geometry
spin geometry, string geometry, fivebrane geometry …
Ingredients
Spin geometry
rotation groups in low dimensions:
see also
String geometry
Fivebrane geometry
Ninebrane geometry
Contents
Idea
The spin group in dimension 5.
Properties
Exceptional isomorphism
Proposition
There is an exceptional isomorphism
between Spin(5) and the quaternionic unitary group .
This is an indirect consequence of triality, see e.g. Čadek-Vanžura 97. Alternatively, it can be shown as follows.
Let be a 4-dimensional complex vector space with an inner product and a compatible complex volume form. As explained here, this structure can be used to define a conjugate-linear Hodge star operator on whose and eigenspaces, say , are each 6-dimensional real inner product spaces. Thus, the group acts as linear transformations of that preserve the inner product, giving a homomorphism . In fact maps in a 2-1 and onto way to . Taking this shows .
Now suppose is additionally equipped with an complex symplectic structure, i.e. a nondegenerate skew-symmetric complex-bilinear form . The subgroup of preserving this extra structure is isomorphic to the compact symplectic group , which is also the quaternionic unitary group. This subgroup acts on and preserving . Since is compact, every invariant subspace has an invariant complement, so one or both of the 6-dimensional subspaces and must have a 5-dimensional subspace invariant under the action of . This shows that the double cover restricts to a 2-1 homomorphism . Since
the differential , being injective, must also be surjective. Thus is actually a double cover. Since is connected this implies .
Action on quaternionic Hopf fibration
Proposition
(Spin(5)-equivariance of quaternionic Hopf fibration)
Consider
-
the Spin(5)-action on the 4-sphere which is induced by the defining action on under the identification ;
-
the Spin(5)-action on the 7-sphere which is induced under the exceptional isomorphism (from Prop. ) by the canonical left action of on via .
Then the quaternionic Hopf fibration is equivariant with respect to these actions.
This is almost explicit in Porteous 95, p. 263
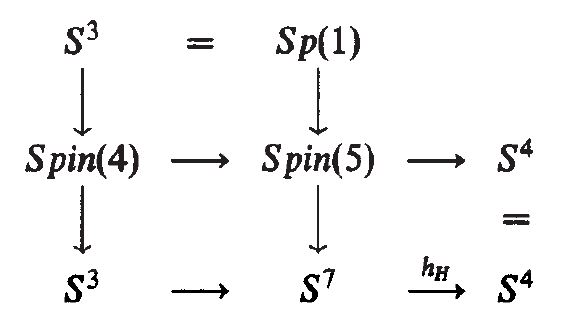
Cohomology
Proposition
The integral cohomology ring of the classifying space is spanned by two generators
-
the linear combination of the half the second Pontryagin class with half the cup product-square of the first Pontryagin class:
This is a special case of the general statement in Pittie 91, see e.g. Kalkkinen 06, Section 3).
Proposition
Let
be the spherical fibration of classifying spaces induced from the canonical inclusion of Spin(4) into Spin(5) and using that the 4-sphere is equivalently the coset space (this Prop.).
Then the fiber integration of the odd cup powers of the Euler class (see this Prop) are proportional to cup powers of the second Pontryagin class
for instance
while the fiber integration of the even cup powers vanishes
Coset spaces
coset space-structures on n-spheres:
| standard: | |
|---|---|
| this Prop. | |
| this Prop. | |
| this Prop. | |
| exceptional: | |
| Spin(7)/G₂ is the 7-sphere | |
| since Spin(6) SU(4) | |
| since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere | |
| G₂/SU(3) is the 6-sphere | |
| Spin(9)/Spin(7) is the 15-sphere |
see also Spin(8)-subgroups and reductions
homotopy fibers of homotopy pullbacks of classifying spaces:
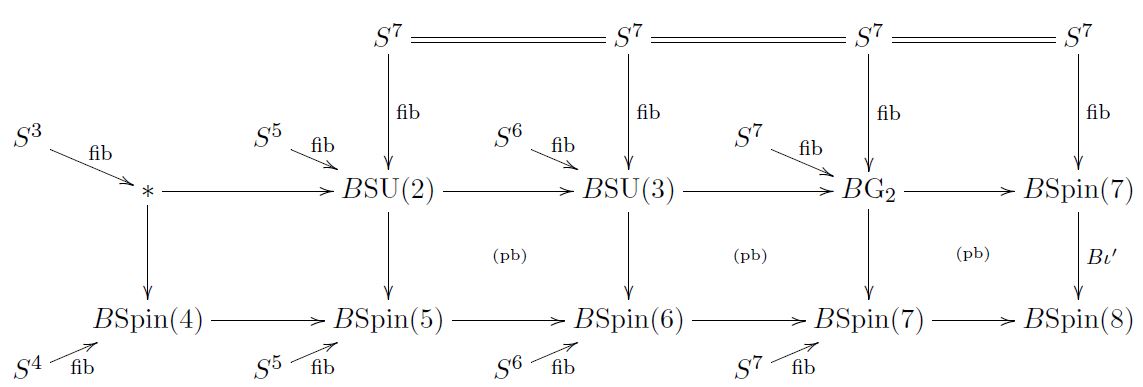
(from FSS 19, 3.4)
-Structure and exceptional geometry
Spin(8)-subgroups and reductions to exceptional geometry
see also: coset space structure on n-spheres
Related concepts
rotation groups in low dimensions:
see also
linebreak
References
-
Ian Porteous, Clifford Algebras and the Classical Groups, Cambridge Studies in Advanced Mathematics, Cambridge University Press (1995)
-
Martin Čadek, Jiří Vanžura, On and -structures in 8-dimensional vector bundles, Publicacions Matemàtiques Vol. 41, No. 2 (1997), pp. 383-401 (jstor:43737249)
-
Raoul Bott, Alberto Cattaneo, Integral Invariants of 3-Manifolds, J. Diff. Geom. 48 (1998) 91-133 [arXiv:dg-ga/9710001, doi:10.4310/jdg/1214460608]
-
Harsh Pittie, The integral homology and cohomology rings of SO(n) and Spin(n), Journal of Pure and Applied Algebra Volume 73, Issue 2, 19 August 1991, Pages 105–153 (doi:10.1016/0022-4049(91)90108-E)
-
Jussi Kalkkinen, Global Spinors and Orientable Five-Branes, JHEP 0609: 028, 2006 (arXiv:hep-th/0604081)
Last revised on June 23, 2023 at 06:02:33. See the history of this page for a list of all contributions to it.