nLab Spin(6)

Idea

The spin group in dimension 6.

Properties

Exceptional isomorphism

Proposition

There is an exceptional isomorphism

between Spin(6) and SU(4), reflecting, under the classification of simple Lie groups, the coincidence of the Dynkin diagrams “D3” and A3.

(e.g. Figueroa-O’Farrill 10, Lemma 8.1)

One way to see the isomorphism $\mathrm{Spin}(6) \cong \mathrm{SU}(4)$ is as follows. Let $V$ be a 4-dimensional complex vector space with an inner product and a compatible complex volume form, meaning an element of the exterior product $\Lambda^4 V$ whose norm is 1 in the norm coming from the inner product on $V$. The inner product defines a conjugate-linear isomorphism $V \cong V^\ast$ (with the complex dual vector space) that together with the complex volume form can be used to define a conjugate-linear Hodge star operator on $\Lambda^2 V$. This Hodge star operator squares to the identity, and its $+1$ and $-1$ eigenspaces, say $\Lambda_{\pm}^2 V$, each become 6-dimensional real inner product spaces in a natural way. Thus, the group $\mathrm{SU}(V)$, consisting of all complex-linear transformations of $V$ that preserve the inner product and complex volume form, acts as linear transformations of $\Lambda_+^2 V$ that preserve the inner product, giving a homomorphism $\rho: \mathrm{SU}(V) \to \mathrm{O}(\Lambda_+^2 V)$. Since $\mathrm{SU}(V)$ is connected we in fact have $\rho: \mathrm{SU}(V) \to \mathrm{SO}(\Lambda_+^2 V)$.

Specializing to the case $V = \mathbb{C}^4$ we get a Lie group homomorphism $\rho: \mathrm{SU}(4) \to \mathrm{SO}(6)$. Since $d\rho$ is nonzero and $\mathrm{SU}(4)$ is simple, $d\rho$ must be injective. Since

$$\mathrm{dim}(\mathrm{SU}(4)) = 15 = \mathrm{dim}(\mathrm{SO}(6)),$$

$d\rho$ must also be surjective. Since $\mathrm{SO}(6)$ is connected and $d\rho$ is a bijection, $\rho$ must be a covering map. Since $\rho(\pm 1) = 1$, $\rho$ exhibits $\mathrm{SU}(4)$ as a connected cover of $\mathrm{SO}(6)$ that is at least a double cover. But the universal cover of $\mathrm{SO}(6)$, namely $\mathrm{Spin}(6)$, is only a double cover. Thus $\mathrm{SU}(4)$ is a double cover of $\mathrm{SO}(6)$, and $\mathrm{SU}(4) \cong \mathrm{Spin}(6)$.

Coset spaces

coset space-structures on n-spheres:

standard:
$S^{n-1} \simeq_{diff} SO(n)/SO(n-1)$	this Prop.
$S^{2n-1} \simeq_{diff} SU(n)/SU(n-1)$	this Prop.
$S^{4n-1} \simeq_{diff} Sp(n)/Sp(n-1)$	this Prop.
exceptional:
$S^7 \simeq_{diff} Spin(7)/G_2$	Spin(7)/G₂ is the 7-sphere
$S^7 \simeq_{diff} Spin(6)/SU(3)$	since Spin(6) $\simeq$ SU(4)
$S^7 \simeq_{diff} Spin(5)/SU(2)$	since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere
$S^6 \simeq_{diff} G_2/SU(3)$	G₂/SU(3) is the 6-sphere
$S^15 \simeq_{diff} Spin(9)/Spin(7)$	Spin(9)/Spin(7) is the 15-sphere

see also Spin(8)-subgroups and reductions

homotopy fibers of homotopy pullbacks of classifying spaces:

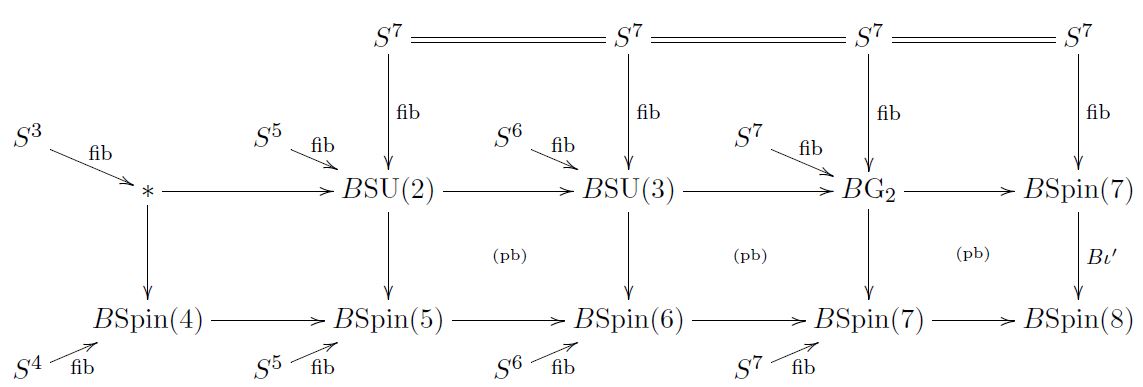
(from FSS 19, 3.4)

$G$-Structure and exceptional geometry

Spin(8)-subgroups and reductions to exceptional geometry

reduction	from spin group	to maximal subgroup
Spin(7)-structure	Spin(8)	Spin(7)
G₂-structure	Spin(7)	G₂
CY3-structure	Spin(6)	SU(3)
SU(2)-structure	Spin(5)	SU(2)
generalized reduction	from Narain group	to direct product group
generalized Spin(7)-structure	$Spin(8,8)$	$Spin(7) \times Spin(7)$
generalized G₂-structure	$Spin(7,7)$	$G_2 \times G_2$
generalized CY3	$Spin(6,6)$	$SU(3) \times SU(3)$

see also: coset space structure on n-spheres

Related concepts

rotation groups in low dimensions:

Dynkin label	sp. orth. group	spin group	pin group	semi-spin group
	SO(2)	Spin(2)	Pin(2)
B1	SO(3)	Spin(3)	Pin(3)
D2	SO(4)	Spin(4)	Pin(4)
B2	SO(5)	Spin(5)	Pin(5)
D3	SO(6)	Spin(6)
B3	SO(7)	Spin(7)
D4	SO(8)	Spin(8)		SO(8)
B4	SO(9)	Spin(9)
D5	SO(10)	Spin(10)
B5	SO(11)	Spin(11)
D6	SO(12)	Spin(12)
	$\vdots$	$\vdots$
D8	SO(16)	Spin(16)		SemiSpin(16)
	$\vdots$	$\vdots$
D16	SO(32)	Spin(32)		SemiSpin(32)

see also

• Spin(5).Spin(3)

• finite rotation groups

• ADE-classification

• U(1), SU(2), SU(3), SU(5)

References

• José Figueroa-O'Farrill, PG course on Spin Geometry lecture 8: Parallel and Killing spinors, 2010 (pdf)