nLab Spin(9)/Spin(7) is the 15-sphere

Statement

The coset space of Spin(9) by Spin(7) is homeomorphic to the 15-sphere:

$$Spin(9)/Spin(7) \;\simeq\; S^15 \,.$$

This coset realization features in the octonionic Hopf fibration, making manifest its $Spin(9)$-equivariance (Ornea-Parton-Piccinni-Vuletescu 12, p. 7).

Related concepts

coset space-structures on n-spheres:

standard:
$S^{n-1} \simeq_{diff} SO(n)/SO(n-1)$	this Prop.
$S^{2n-1} \simeq_{diff} SU(n)/SU(n-1)$	this Prop.
$S^{4n-1} \simeq_{diff} Sp(n)/Sp(n-1)$	this Prop.
exceptional:
$S^7 \simeq_{diff} Spin(7)/G_2$	Spin(7)/G₂ is the 7-sphere
$S^7 \simeq_{diff} Spin(6)/SU(3)$	since Spin(6) $\simeq$ SU(4)
$S^7 \simeq_{diff} Spin(5)/SU(2)$	since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere
$S^6 \simeq_{diff} G_2/SU(3)$	G₂/SU(3) is the 6-sphere
$S^15 \simeq_{diff} Spin(9)/Spin(7)$	Spin(9)/Spin(7) is the 15-sphere

see also Spin(8)-subgroups and reductions

homotopy fibers of homotopy pullbacks of classifying spaces:

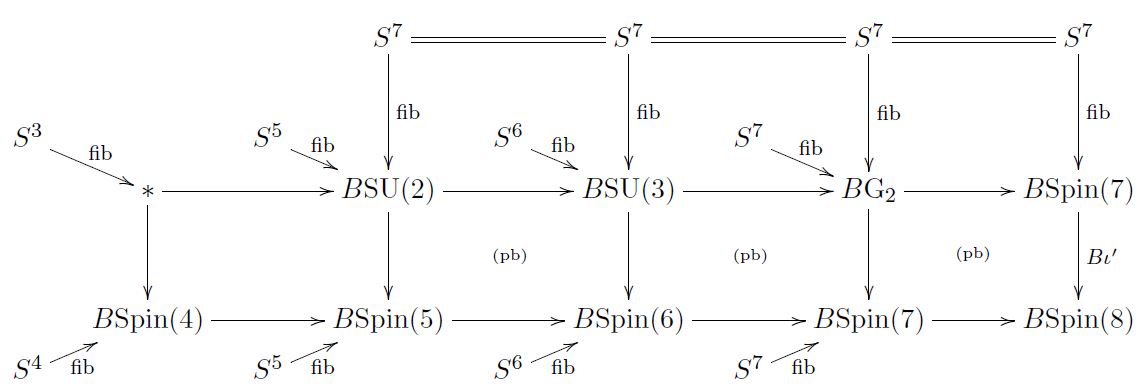
(from FSS 19, 3.4)

References

• Alfred Gray, Paul S. Green, p. 2 of Sphere transitive structures and the triality automorphism, Pacific J. Math. Volume 34, Number 1 (1970), 83-96 (euclid:1102976640)

• Liviu Ornea, Maurizio Parton, Paolo Piccinni, Victor Vuletescu, Spin(9) geometry of the octonionic Hopf fibration, Transformation Groups (2013) 18: 845 (arXiv:1208.0899, doi:10.1007/s00031-013-9233-x)