nLab Spin(5)/SU(2) is the 7-sphere

Statement

The coset space of Spin(5) by its subgroup SU(2) is diffeomorphic to the standard 7-sphere:

(1)$$Spin(5)/SU(2) \;\simeq_{diff}\; S^7 \,.$$

This is however not an isometry to the standard Riemannian manifold-structure (“round n-sphere”), whence one speaks of a squashed n-sphere.

The identification (1) follows via the exceptional isomorphisms

Spin(5)$\simeq$ Sp(2)

and

SU(2)$\simeq$ Sp(1)

as a special case of the general statement

$$S^{4n-1} \simeq_{diff} Sp(n)/Sp(n-1)$$

(see this Prop.).

Related concepts

coset space-structures on n-spheres:

standard:
$S^{n-1} \simeq_{diff} SO(n)/SO(n-1)$	this Prop.
$S^{2n-1} \simeq_{diff} SU(n)/SU(n-1)$	this Prop.
$S^{4n-1} \simeq_{diff} Sp(n)/Sp(n-1)$	this Prop.
exceptional:
$S^7 \simeq_{diff} Spin(7)/G_2$	Spin(7)/G₂ is the 7-sphere
$S^7 \simeq_{diff} Spin(6)/SU(3)$	since Spin(6) $\simeq$ SU(4)
$S^7 \simeq_{diff} Spin(5)/SU(2)$	since Sp(2) is Spin(5) and Sp(1) is SU(2), see Spin(5)/SU(2) is the 7-sphere
$S^6 \simeq_{diff} G_2/SU(3)$	G₂/SU(3) is the 6-sphere
$S^15 \simeq_{diff} Spin(9)/Spin(7)$	Spin(9)/Spin(7) is the 15-sphere

see also Spin(8)-subgroups and reductions

homotopy fibers of homotopy pullbacks of classifying spaces:

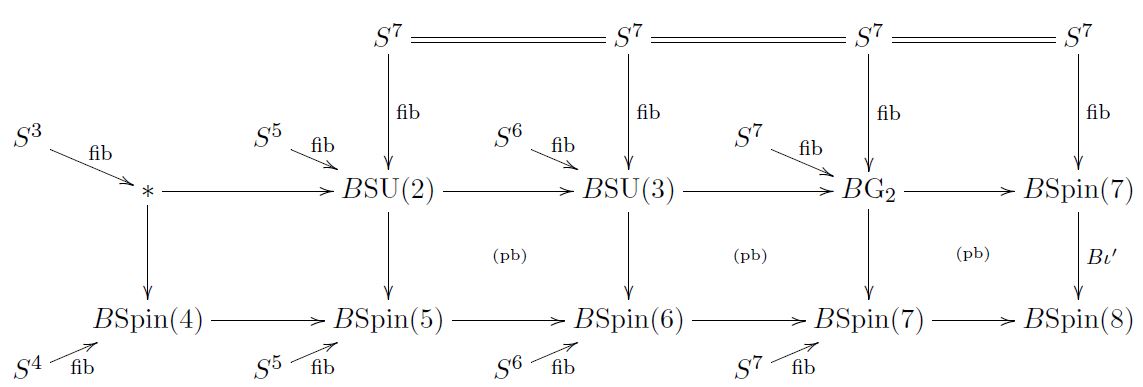
(from FSS 19, 3.4)

References

• Alfred Gray, Paul S. Green, p. 2 of Sphere transitive structures and the triality automorphism, Pacific J. Math. Volume 34, Number 1 (1970), 83-96 (euclid:1102976640)

Discussion of this squashed 7-sphere coset space as a fiber for KK-compactification of 11-dimensional supergravity:

• M. A. Awada, Mike Duff, Christopher Pope, $N=8$ Supergravity Breaks Down to $N=1$, Phys. Rev. Lett. 50, 294 – Published 31 January 1983 (doi:10.1103/PhysRevLett.50.294)

• Mike Duff, Bengt Nilsson, Christopher Pope, Spontaneous Supersymmetry Breaking by the Squashed Seven-Sphere, Phys. Rev. Lett. 50, 2043 – Published 27 June 1983; Erratum Phys. Rev. Lett. 51, 846 (doi:10.1103/PhysRevLett.50.2043)