nLab rational n-sphere
Context
Spheres
Rational homotopy theory
and
rational homotopy theory (equivariant, stable, parametrized, equivariant & stable, parametrized & stable)
dg-Algebra
Rational spaces
PL de Rham complex
Sullivan models
Examples of Sullivan models in rational homotopy theory:
Related topics
Contents
Idea
The rational -sphere is the rationalization of the n-sphere.
As a topological space this is a rational topological space closest to the -sphere, in the sense of rational homotopy theory.
Sullivan models
The minimal Sullivan model of a sphere of odd dimension is the dg-algebra with a single generator in degre and vanishing differential
The minimal Sullivan model of a sphere of even dimension, for , is the dg-algebra with a generator in degree and another generator in degree with the differential defined by
One may understand this form the central fact of rational homotopy theory (the proposition here):
An -sphere has rational cohomology concentrated in degree . Hence its minimal Sullivan model needs at least one closed generator in that degree. In the odd dimensional case one such is already sufficient, since the wedge square of that generator vanishes and hence produces no higher degree cohomology classes. But in the even degree case the wedge square needs to be canceled in cohomology. That is accomplished by the second generator .
Again by that proposition, this now implies that the rational homotopy groups of spheres are concentrated, in degree for the odd -dimensional spheres, and in degrees and in for the even -dimensional spheres. (These are the non-torsion homotopy groups of spheres appearing in the Serre finiteness theorem.)
For instance the 4-sphere has rational homotopy in degree 4 and 7. The one in degree 7 being represented by the quaternionic Hopf fibration.
Hence, odd dimensional -spheres are rationally homotopy equivalent to Eilenberg-MacLane spaces , while even-dimensional spheres are not.
Applications
Hopf invariant
Proposition
By standard results in rational homotopy theory, every continuous function
corresponds to a unique dgc-algebra homomorphism
between Sullivan models of n-spheres.
The unique free coefficient of this homomorphism is the Hopf invariant of :
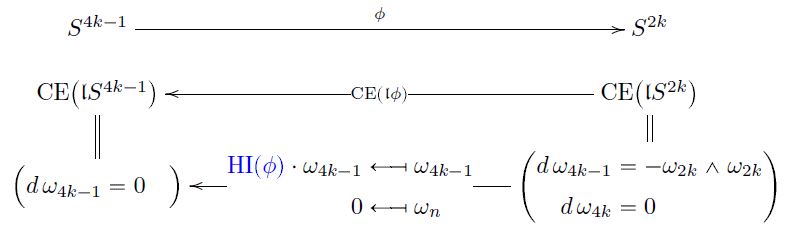
Related concepts
-
The non-abelian generalized cohomology theory represented by rational n-spheres is rational Cohomotopy cohomology theory.
Examples of Sullivan models in rational homotopy theory:
References
-
Alan J. Deschner, Exp. 3.5 (a) in: Sullivan’s theory of minimal models, MSc thesis, Univ. British Columbia (1976) [doi:10.14288/1.0080132, pdf]
-
Yves Félix, Stephen Halperin, Jean-Claude Thomas, p. 142 in: Rational Homotopy Theory, Graduate Texts in Mathematics, 205, Springer-Verlag, 2000 (doi:10.1007/978-1-4613-0105-9)
-
Luc Menichi, Section 1.2 in: Rational homotopy – Sullivan models, in: Free Loop Spaces in Geometry and Topology, IRMA Lect. Math. Theor. Phys. 24, EMS (2015) 111-136 [doi:10.4171/153, arXiv:1308.6685]
Last revised on September 1, 2025 at 00:19:46. See the history of this page for a list of all contributions to it.