nLab fundamental theorem of dg-algebraic rational homotopy theory

Idea

The fundamental theorem of rational homotopy theory modeled by dgc-algebras.

Preliminaries

Definition

(nilpotent and finite rational homotopy types)

Write

(1)$$Ho \big( SimplicialSets_{Qu} \big)^{fin_{\mathbb{Q}}}_{\geq 1, nil} \overset{ \phantom{AAA} }{\hookrightarrow} Ho \big( SimplicialSets_{Qu} \big)$$

for the full subcategory of the classical homotopy category (homotopy category of the classical model structure on simplicial sets) on those homotopy types $X$ which are

• connected: $\pi_0(X) = \ast$;

• nilpotent: the fundamental group $\pi_1(X)$ is a nilpotent group and the higher homotopy groups are nilpotent modules over it;

• rationally of finite type: the rational cohomology-groups are finite-dimensional, $dim_{\mathbb{Q}}\big( H^n(X;,\mathbb{Q}) \big) \lt \infty$, for all $n \in \mathbb{N}$.

and

(2)$$Ho \big( SimplicialSets_{Qu} \big)^{\mathbb{Q}, fin_{\mathbb{Q}}}_{\geq 1, nil} \overset{ \phantom{AAA} }{\hookrightarrow} Ho \big( SimplicialSets_{Qu} \big)$$

for the further full subcategory on those homotopy types that are already rational.

Similarly, write

(3)$$Ho \big( DiffGradedCommAlgebras^{\geq 0}_{\mathbb{Q}} \big)_{fin}^{\geq 1} \overset{ \phantom{AAA} }{\hookrightarrow} Ho \big( DiffGradedCommAlgebras^{\geq 0}_{\mathbb{Q}} \big)$$

for the full subcategory of the homotopy category of the projective model structure on connective dgc-algebras on those dgc-algebras $A$ over the rational numbers which are

• connected: $H^0(A) \simeq \mathbb{Q}$

• finite type: the cochain cohomology groups are finite dimensional, $dim_{\mathbb{Q}}\big( H^n(A) \big) \lt \infty$, for all $n \in \mathbb{N}$.

(Bousfield-Gugenheim 76, 9.2)

Statement

Proposition

(fundamental theorem of dg-algebraic rational homotopy theory)

The derived adjunction

$$Ho \left( \big( DiffGradedCommAlgebras^{\geq 0}_{\mathbb{Q}} \big)^{op}_{proj} \right) \underoverset { \underset {\;\;\; \mathbb{R} exp_{PL} \;\;\;} {\longrightarrow} } { \overset {\;\;\; \mathbb{L} \Omega^\bullet_{PLdR}\;\;\;} {\longleftarrow} } {\bot} Ho \big( SimplicialSets_{Qu} \big)$$

of the Quillen adjunction between simplicial sets and connective dgc-algebras (whose left adjoint is the PL de Rham complex-functor) has the following properties:

• on connected, nilpotent rationally finite homotopy types $X$ (1) the derived adjunction unit is rationalization

  $$\array{ Ho \big( SimplicialSets_{Qu} \big)^{fin_{\mathbb{Q}}}_{\geq 1, nil} & \overset{ }{\longrightarrow} & Ho \big( SimplicialSets_{Qu} \big)^{\mathbb{Q}, fin_{\mathbb{Q}}}_{\geq 1, nil} \\ X &\mapsto& \mathbb{R}\exp_{PL} \circ \Omega^\bullet_{PLdR}(X) }$$
  $$X \underoverset {\eta_X^{der}} {rationalization} {\longrightarrow} \mathbb{R}\exp_{PL} \circ \Omega^\bullet_{PLdR}(X)$$

• on the full subcategories of nilpotent and finite rational homotopy types from Def. it restricts to an equivalence of categories:

  $$Ho \left( \big( DiffGradedCommAlgebras^{\geq 0}_{\mathbb{Q}} \big)^{op}_{proj} \right)^{\geq 1}_{fin} \underoverset { \underset {\;\;\; \mathbb{R} exp_{PL} \;\;\;} {\longrightarrow} } { \overset {\;\;\; \mathbb{L} \Omega^\bullet_{PLdR}\;\;\;} {\longleftarrow} } {\simeq} Ho \big( SimplicialSets_{Qu} \big)^{\mathbb{Q}, fin_{\mathbb{Q}}}_{\geq 1, nil}$$

(Bousfield-Gugenheim 76, Theorems 9.4 & 11.2)

Change of scalars

Often it is desireable to work with dgc-algebras not over the rational numbers but over the real numbers, because these relate to de Rham theory (e.g.: the PL de Rham complex of a smooth manifold is equivalent to the de Rham complex). While a PL de Rham complex-Quillen adjunction $\Omega^\bullet_{\mathrm{P}\!k\!\mathrm{LdR}} \dashv \exp_{\mathrm{P}\!k\!\mathrm{L}}$ (“piecewise $k$-linear”) exists over all ground fields $k$ of characteristic zero, with induced derived adjunction

$$Ho \Big( \big( DGCAlgebras^{\geq 0}_{k} \big)^{op}_{proj} \Big) \underoverset {\underset{\mathbb{R} exp_{\mathrm{P}\!k\!\mathrm{L}}}{\longrightarrow}} {\overset{\mathbb{L} \Omega^\bullet_{\mathrm{P}\!k\!\mathrm{LdR}}}{\longleftarrow}} {\bot} Ho \big( SimplicialSets_{Qu} \big) \,,$$

this does not model $k$-localization of spaces unless $k = \mathbb{Q}$. However, it does still relate to rationalization under extension of scalars, given by the derived adjunction (via this Prop.)

$$Ho \Big( \big( DGCAlgebras^{\geq 0}_{k} \big)^{op}_{proj} \Big) \underoverset { \underset{ \mathbb{R}\big( (-)\otimes_{\mathbb{Q}}\mathbb{R} \big) }{ \longrightarrow } } { \overset{ \mathbb{L} res_{\mathbb{Q}} }{ \longleftarrow } } {\bot} Ho \Big( \big( DGCAlgebras^{\geq 0}_{\mathbb{Q}} \big)^{op}_{proj} \Big) \,,$$

in that the following holds:

Proposition

For $k$ be a field of characteristic zero, the following diagram of derived functors commutes up to natural isomorphism:

This is effectivley the statement of Bousfield&Gugenheim 1976, Lem. 11.7.

This state of affairs may be recast as follows (FSS 2020):

For any field $k$ of characteristic zero, abbreviate

$$L_k \;\coloneqq\; \mathbb{R} exp_{\mathrm{P}k\mathrm{L}} \circ \mathbb{L} \Omega^\bullet_{\mathrm{P}kLdR} \,,$$

keeping in mind that this is a localization of spaces only if $k = \mathbb{Q}$.

Then for $X, A \in Ho(sSet)^{fin_{\mathbb{Q}}}_{\geq 1, nil}$ a pair of connected nilpotent ℚ-finite homotopy types, define the $k$-Chern-Dold character on the non-abelian $A$-cohomology of $X$ to be the cohomology operation induced by the derived adjunction unit of the PL de Rham adjunction (this Prop.):

(4)$$ch^k_A(X) \;\colon\; H(X;\, A) \;\xrightarrow{ \;\; H(X;\, \mathbb{D}\eta^{\mathrm{P}k\mathrm{L}_A}) \;\; }\; H(X;\, L_k A) \,.$$

Moreover, define extension of scalars on non-abelian rational cohomology to be the comoposite

(5)$$\array{ H(X;\, L_{\mathbb{Q}}A) &\xrightarrow{ (-) \otimes_{{}_{\mathbb{Q}}} k }& H(X;\, L_{k}A) \\ {}^{\mathllap{ \widetilde{(-)} }} \big\downarrow {}^{\mathrlap{\simeq}} && {}^{\mathllap{\simeq}} \big\uparrow {}^{\mathrlap{ \widetilde{(-)} }} \\ H \big( \mathbb{D}\Omega^\bullet_{\mathrm{P}\mathbb{Q}\mathrm{LdR}}(X); \, \mathbb{D}\Omega^\bullet_{\mathrm{P}\mathbb{Q}\mathrm{LdR}}(A) \big) & \xrightarrow{ \mathbb{D} \big( (-) \otimes_{{}_{\mathbb{Q}}} k \big) } & H \big( \mathbb{D}\Omega^\bullet_{\mathrm{P}k\mathrm{LdR}}(X); \, \mathbb{D}\Omega^\bullet_{\mathrm{P}k\mathrm{LdR}}(A) \big) }$$

(where $H(-;\,-) \coloneqq Ho(-,\,-)$ denotes hom-sets in the respective homotopy category)

of:

1. the hom-isomorphisms of the derived PL de Rham adjunction;

2. the corresponding hom-component of the derived functor of extension of scalars (this Prop.).

(This is essentially the construction of “tensoring a homotopy type with $\mathbb{R}$” that is mentioned in DGMS 1975, Footnote 5.)

Then:

Proposition

The $k$-Chern-Dold character (4) factors through the rational Chern-Dold character via the extension-of-scalars-transformation (5).

$$ch^k_A(X) \;=\; \big( (-)\otimes_{{}_{\mathbb{Q}}} k \big) \,\circ\, ch^{\mathbb{Q}}_A(X) \,.$$

Proof

Consider the following diagram of hom-sets (shown for $k = \mathbb{R}$, just for definiteness):

(diagram from FSS 20)

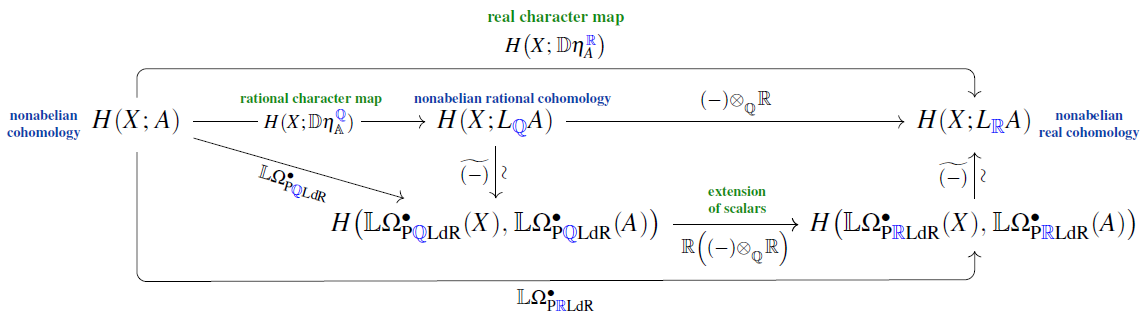
Here:

• the commutativity of the bottom part is Prop. ;

• the triangle on the left as well as as the outer diagram commute by basic properties of adjoint functors (this Lemma);

• the square on the right commutes by definition (5);

Together this implies that the top rectangle commutes, which is the claim to be shown.

Related concepts

• fundamental theorem of equivariant dg-algebraic rational homotopy theory

• real homotopy theory

References

The full-blown equivalence first appears in

• Aldridge Bousfield, Victor Gugenheim, On PL deRham theory and rational homotopy type, Memoirs of the AMS 179 (1976) [ams:memo-8-179]

Concise review (without model category-theory, but discussion as an sSet-enriched adjunction nonetheless) and generalization both to Borel-equivariant rational homotopy theory (of covering spaces of non-nilpotent spaces), as well as to real homotopy theory:

• Edgar Brown, Robert H. Szczarba, Real and Rational Homotopy Theory, Chapter 17 in: Handbook of Algebraic Topology, Elsevier, 1995 869-915 (doi:10.1016/B978-044481779-2/50018-3, ZB)

Further related discussion over the real numbers:

• Pierre Deligne, Phillip Griffiths, John Morgan, Dennis Sullivan, Real homotopy theory of Kähler manifolds,

  Inventiones mathematicae volume 29, pages 245–274 (1975) (doi:10.1007/BF01389853)

Re-derivation in a context of derived algebraic geometry:

• Jacob Lurie, Prop. 1.3.3, Cor. 1.3.4 in DAG XIII: Rational and p-Adic Homotopy Theory, 2011 (pdf, pdf)

Review and interpretation in terms of non-abelian Chern-Dold character-theory:

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, The Character Map in Nonabelian Cohomology — Twisted, Differential, Generalizaed, World Scientific (2023) [arXiv:2009.11909, doi:10.1142/13422]