nLab monoid
Context
Category theory
Concepts
Universal constructions
Theorems
Extensions
Applications
Algebra
Algebraic theories
Algebras and modules
Higher algebras
-
symmetric monoidal (∞,1)-category of spectra
Model category presentations
Geometry on formal duals of algebras
Theorems
Monoid theory
monoid theory in algebra:
Contents
Idea
In algebra, by a monoid one means a collection (set) of elements equipped with a binary operation (a “multiplication operation”) which is associative and has a unit element.
Hence monoid structure on a set is a fairly rudimentary form of algebraic structure which underlies many familiar structures considered algebra, such as that of groups (which are monoids with all inverse elements) and rings (which are abelian groups compatibly equipped with a second monoid structure).
Therefore, in the algebraic literature monoids are, conversely, often called unital semi-groups. The root “mono-” in “monoid” refers to the single binary operation (cf. duoid and dioid).
The terminology of magmas is meant to invoke this rudimemtary but foundational nature of basic algebraic structures: Monoids are precisely the unital associative magmas.
The categorification of the notion of monoids is that of monads whose ubiquitous role in mathematics (together with their associated adjoint functors) is hard to overstate.
Definitions
Elementary definition
The classical definition of monoids in Sets, as a unital associative magma:
Definition
A monoid is a set equipped with the structure if
-
(binary operation) a map from the Cartesian product of the set with itself to itself
-
(neutral element) an element
such that the following equations are satisfied
In a monoidal category
See monoid in a monoidal category.
In terms of string diagrams
The data of a monoid may be written in string diagrams as:
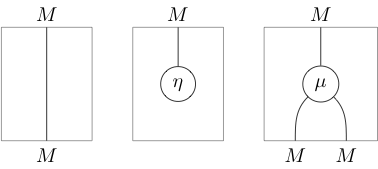
Thanks to the distinctive shapes, one can usually omit the labels:
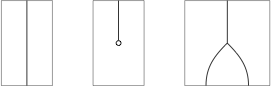
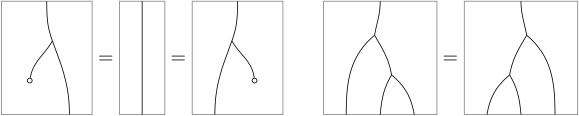
The axioms and then appear as:
As a one-object category
Equivalently, and more efficiently, we may say that a (classical) monoid is the hom-set of a category with a single object, equipped with the structure of its unit element and composition.
More tersely, one may say that a monoid is a category with a single object, or more precisely (to get the proper morphisms and -morphisms) a pointed category with a single object. But taking this too literally may create conflicts in notation. To avoid this, for a given monoid , we write for the corresponding category with single object and with as its hom-set: the delooping of , so that . This realizes every monoid as a monoid of endomorphisms.
Similarly, a monoid in may be defined as the hom-object of a -enriched category with a single object, equipped with its composition and identity-assigning morphisms; and so on, as in the classical (i.e. -enriched) case.
For more on this see also group.
As a strict monoidal category
An alternate way to view a monoid as a category is as a discrete strict monoidal category where the elements of the monoid are the objects of , the binary operation of the monoid provides the tensor product bifunctor, and the identity of the monoid is the unit object. Preordered monoids then yield (non-discrete) strict monoidal categories with the morphisms witnessing the preorder in the usual way.
-Monoids over an -Operad
The notion of associative monoids discussed above are controled by the associative operad. More generally in higher algebra, for any operad or (infinity,1)-operad, one can consider -monoids. (Lurie, def. 2.4.2.1)
These are closely related to (infinity,1)-algebras over an (infinity,1)-operad with respect to (Lurie, prop. 2.4.2.5).
Properties
Finite products (and sums)
Let be a monoid, and let be the free monoid on with canonical function taking the elements of to the generators in . The finite product operation on is a monoid homomorphism
from to , where:
If is written additively instead of multiplicatively , the operation is called finite sum, and is defined as
from to , where:
Examples
- A monoid in which every element has an inverse is a group. For that reason monoids are often known (especially outside category theory) as semi-groups. (But this term is often extended to monoids without identities, that is to sets equipped with any associative operation.)
- The set of endomorphisms of a given object in a category has a canonical monoid structure given by composition.
Remarks on notation
It can be important to distinguish between a -tuply monoidal structure and the corresponding -tuply degenerate category, even though there is a map identifying them. The issue appears here for instance when discussing the universal -bundle in its groupoid incarnation. This is
(where is the action groupoid of acting on itself). On the left we crucially have as a monoidal 0-category, on the right as a once-degenerate 1-category. Without this notation we cannot even write down the universal -bundle!
Or take the important difference between group representations and group 2-algebras, the former being functors , the latter functors . Both these are very important.
Or take an abelian group and a codomain like . Then there are 3 different things we can sensibly consider, namely 2-functors
and
All of these concepts are different, and useful. The first one is an object in the group 3-algebra of . The second is a pseudo-representation of the group . The third is a representations of the 2-group . We have notation to distinguish this, and we should use it.
Finally, writing for the 1-object -groupoid version of an -monoid makes notation behave nicely with respect to nerves, because then realization bars simply commute with the s in the game: .
This behavior under nerves shows also that, generally, writing gives the right intuition for what an expression means. For instance, what’s the “geometric” reason that a group representation is an arrow ? It’s because this is, literally, equivalently thought of as the corresponding classifying map of the vector bundle on which is -associated to the universal -bundle:
the -associated vector bundle to the universal -bundle is, in its groupoid incarnations,
where is the vector space that is representing on, and this is classified by the representation in that this is the pullback of the universal -bundle
In summary, it is important to make people understand that groups can be identified with one-object groupoids. But next it is important to make clear that not everything that can be identified should be, for instance concerning the crucial difference between the category in which lives and the 2-category in which lives.
Related concepts
-
monoid, internal monoid/monoid object,
References
Beware that the term “monoid” was first used by
- Arthur Cayley, Second and Third Memoirs on Skew Surfaces, Otherwise Scrolls, Phil. Trans. (1863 and 1869)
for certain surfaces, quite unrelated to the modern meaning of the term.
Instead, what are now called monoids (unital associative magmas) were called groupoids (now clashing with the modern use of groupoid) by
- Garrett Birkhoff, Hausdorff Groupoids, Annals of Mathematics, Second Series 35 2 (1934) 351-360 [jstor:1968437, doi:10.2307/1968437]
The modern terminology “monoid” for unital associative magmas is (according to Hollings 2009, p. 529) due to
For more on the history of the notion:
-
Christopher Hollings, The Early Development of the Algebraic Theory of Semigroups, Archive for History of Exact Sciences 63 (2009) 497–536 [doi:10.1007/s00407-009-0044-3]
-
Math.SE, Who invented Monoid?
Exposition of basics of monoidal categories and categorical algebra:
Properties of monoids expressed through properties of their toposes of presheaves:
- Jens Hemelaer, Morgan Rogers, Monoid Properties as Invariants of Toposes of Monoid Actions, arXiv:2004.10513.
Formalization of monoid objects as mathematical structures in proof assistants:
in a context of plain Agda:
- Martín Escardó, The Types of Magmas and Monoids, §4 in: Introduction to Univalent Foundations of Mathematics with Agda [arXiv:1911.00580, webpage]
Last revised on July 10, 2024 at 18:52:02. See the history of this page for a list of all contributions to it.