nLab associahedron

Idea

The associahedra or Stasheff polytopes $\{K_n\}$ are CW complexes that naturally arrange themselves into a topological operad that resolves the standard associative operad: an A-infinity-operad.

The vertices of $K_n$ correspond to ways in which one can bracket a product of $n$ variables. The edges correspond to rebracketings, the faces relate different sequences of rebracketings that lead to the same result, and so on.

The associahedra were introduced by Jim Stasheff in order to describe topological spaces equipped with a multiplication operation that is associative up to every higher coherent homotopy.

Definition

Here is the rough idea, copied, for the moment, verbatim from Markl94 p. 26 (for more details see references below):

For $n \geq 1$ the associahedron $K_n$ is an $(n-2)$-dimensional polyhedron whose $i$-dimensional cells are, for $0 \leq i \leq n-2$, indexed by all (meaningful) insertions of $(n-i-2)$ pairs of brackets between $n$ independent indeterminates, with suitably defined incidence maps.

Simplicially${ }$ subdivided associahedra (complete with simplicial operadic structure) can be presented efficiently in terms of an abstract bar construction. Let $\mathcal{O}: Set/\mathbb{N} \to Set/\mathbb{N}$ be the monad which takes a graded set $X$ to the non-permutative non-unital operad freely generated by $X$, with monad multiplication denoted $m: \mathcal{O}\mathcal{O} \to \mathcal{O}$. Let $t_+$ be the graded set $\{X_n\}_{n \geq 0}$ that is empty for $n = 0, 1$ and terminal for $n \geq 2$; this carries a unique non-unital non-permutative operad structure, via a structure map $\alpha: \mathcal{O}t_+ \to t_+$. The bar construction $B(\mathcal{O}, \mathcal{O}, t_+)$ is an (augmented) simplicial graded set (an object in $Set^{\Delta^{op} \times \mathbb{N}}$) whose face maps take the form

$$\ldots \mathcal{O}\mathcal{O}\mathcal{O}t_+ \stackrel{\stackrel{\overset{m\mathcal{O} t_+}{\to}}{\underset{\mathcal{O}m t_+}{\to}}}{\underset{\mathcal{O}\mathcal{O}\alpha}{\to}} \mathcal{O}\mathcal{O}t_+ \stackrel{\overset{m t_+}{\to}}{\underset{\mathcal{O}\alpha}{\to}} \mathcal{O}t_+ \stackrel{\alpha}{\to} t_+.$$

Intuitively, the (graded set of) $0$-cells $\mathcal{O}t_+$ consists of planar trees where each inner node has two or more incoming edges, with trees graded by number of leaves; the extreme points are binary trees [corresponding to complete binary bracketings of words], whereas other trees are barycenters of higher-dimensional faces of Stasheff polytopes. The construction $B(\mathcal{O}, \mathcal{O}, t_+)$ carries a simplicial (non-permutative non-unital) operad structure, where the geometric realization of the simplicial set at grade (or arity) $n$ defines the barycentric subdivision of the Stasheff polytope $K_n$. As the operad structure on $B(\mathcal{O}, \mathcal{O}, t_+)$ is expressed in finite product logic and geometric realization preserves finite products, the (simplicially subdivided) associahedra form in this way the components of a topological operad.

Loday’s realization

Jean-Louis Loday gave a simple formula for realizing the Stasheff polytopes as a convex hull of integer coordinates in Euclidean space (Loday 2004). Let $Y_n$ denote the set of (rooted planar) binary trees with $n+1$ leaves (and hence $n$ internal vertices). For any binary tree $t \in Y_n$, enumerate the leaves by left-to-right order, denoted $\ell_1, \ldots, \ell_{n+1}$, and enumerate the internal vertices as $v_1, \ldots, v_n$ where $v_i$ is the closest common ancestor of $\ell_i$ and $\ell_{i+1}$. Define a vector $M(t) \in \mathbb{R}^n$ whose $i$th coordinate is the product $a_i b_i$ of the number $a_i$ of leaves that are left descendants of $v_i$ and the number $b_i$ of leaves that are right descendants of $v_i$.

Theorem (Loday)

The convex hull of the points $\{ M(t) \in \mathbb{R}^n \mid t \in Y_n \}$ is a realization of the Stasheff polytope of dimension $n-1$, and is included in the affine hyperplane $\{(x_1, \ldots, x_n): x_1 + \ldots + x_n = \binom{n}{2}\}$.

Illustrations

• $K_1$ is the empty set, a degenerate case not usually considered.

• $K_2$ is simply the shape of a binary operation:

  $$x \otimes y ,$$

  which we interpret here as a single point.

• $K_3$ is the shape of the usual associator or associative law

  $$(x \otimes y) \otimes z \to x \otimes (y \otimes z) ,$$

  consisting of a single interval.

• $K_4$ The fourth associahedron $K_4$ is the pentagon which expresses the different ways a product of four elements may be bracketed

One can also think of this as the top-level structure of the 4th oriental. This controls in particular the pentagon identity in the definition of monoidal category, as discussed there.

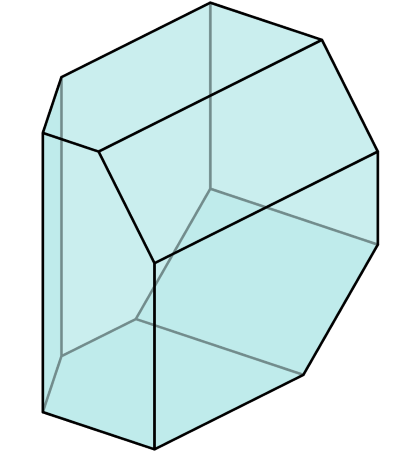
• $K_5$ is the dual polyhedron to the triaugmented triangular prism

(image from the Wikimedia Commons)

• One can rotate and explore Stasheff polyhedra in this interactive associahedron app.

• Illustrations of some polytopes, including $K_5$, can also be found here.

• A template which can be cut out and assembled into a $K_5$ can be found in Appendix B of ChengLauda2004.

Relation to other structures

Relation to orientals

The above list shows that the first few Stasheff polytopes are nothing but the first few orientals. This doesn’t remain true as $n$ increases. The orientals are free strict omega-categories on simplexes as parity complexes. This means that certain interchange cells (e.g., Gray tensorators) show up as thin in the oriental description.

The first place this happens is the sixth oriental: where there are three tensorator squares and six pentagons in Stasheff’s $K_5$, the corresponding tensorator squares coming from $O(5)$ are collapsed.

It was when Todd Trimble made this point to Ross Street that Street began to think about using associahedra to define weak n-categories.

Categorified associahedra

There is a categorification of associahedra discussed in

• S. Saneblidze, R. Umble, Diagonals on the permutahedra, multiplihedra and associahedra, Homology Homotopy Appl. 6(1) (2004) 363–411.
• Stefan Forcey, Quotients of the multiplihedron as categorified associahedra, Homology Homotopy Appl. 10:2 (2008) 227–256 (Euclid)

Tamari lattice

The associahedron is closely related to a structure known as the Tamari lattice, which is especially well-studied in combinatorics. The Tamari lattice $T_n$ can be defined as the poset of all parenthesizations of $n+1$ variables with the order generated by rightwards reassociation $(a b)c \le a(b c)$, or equivalently as the poset of all binary trees with $n$ internal nodes (and hence $n+1$ leaves), with the order generated by rightwards tree rotation. (Note the off-by-one offset from the convention for associahedra: the Tamari lattice $T_n$ corresponds to the associahedron $K_{n+1}$.) It was originally introduced by Dov Tamari in his thesis “Monoïdes préordonnés et chaînes de Malcev” (Université de Paris, 1951), around a decade before Jim Stasheff’s work.¹

As the name suggests, the Tamari lattice also carries the structure of a lattice. This property was originally established by Haya Friedman and Tamari (1967), and later simplified by Samuel Huang and Tamari (1972).

References

The original articles that define associahedra and in which the operad $K$ that gives $A(\infty)$-topological spaces is implicit are

• Jim Stasheff, Homotopy associativity of H-spaces I, Trans. Amer. Math. Soc. 108 (1963), 275–312. (web)

• Jim Stasheff, Homotopy associativity of H-spaces II, Trans. Amer. Math. Soc. 108 (1963), 293–312. (web)

A textbook discussion (slightly modified) is in section 1.6 of the book

• Martin Markl, Steven Shnider, Jim Stasheff, Operads in Algebra, Topology and Physics (web)

Loday’s original article on the Stasheff polytope is

• Jean-Louis Loday, Realization of the Stasheff polytope, Archiv der Mathematik 83 (2004), 267-278. (doi)

Further explanations and references are collected at

• AMS entry on associahedra

• Alexander Postnikov, Permutohedra, associahedra and beyond, math.CO/0507163 pdf

The connection to Tamari lattices as well as other developments are in

• Folkert Müller-Hoissen, Jean Marcel Pallo, Jim Stasheff (editors), Associahedra, Tamari Lattices, and Related Structures: Tamari Memorial Festschrift, Birkhäuser, 2012. (google books)

For a template of $K_5$, see Appendix B of the following.

• Eugenia Cheng, Aaron Lauda, Higher-dimensional categories: an illustrated guidebook, 2004, available here.

For the combinatorics of associahedra, see

• Viviane Pons, Combinatorics of the Permutahedra, Associahedra, and Friends (arXiv:2310.12687)

category: combinatorics

---

1. Jim Stasheff comments on this in an essay titled “How I ‘met’ Dov Tamari” (Tamari Memorial Festschrift 2012), writing that the “so-called Stasheff polytope … more accurately should be called the Tamari or Tamari-Stasheff polytope”. ↩