nLab balanced monoidal category
Context
Monoidal categories
With braiding
With duals for objects
-
category with duals (list of them)
-
dualizable object (what they have)
-
ribbon category, a.k.a. tortile category
With duals for morphisms
With traces
Closed structure
Special sorts of products
Semisimplicity
Morphisms
Internal monoids
Examples
Theorems
In higher category theory
Balanced monoidal categories
Definition
A twist, or balance, in a braided monoidal category is a natural isomorphism from the identity functor on to itself satisfying the following compatibility condition with the braiding :
A balanced monoidal category is a braided monoidal category equipped with such a balance.
Beware that there is an un-related notion of balanced categories.
Properties
In the language of string diagrams, the balancing is represented by a 360-degree twist:
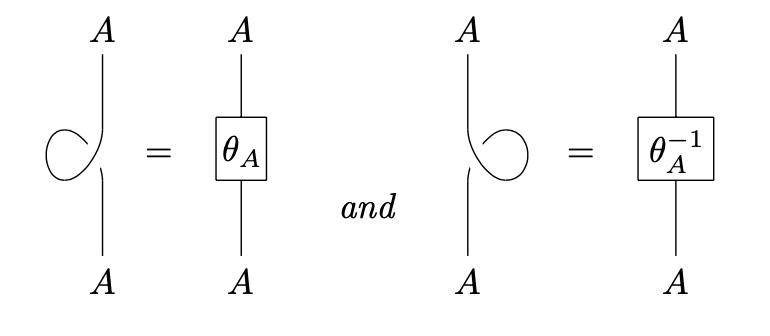
Every symmetric monoidal category is balanced in a canonical way. In fact, the identity natural transformation on the identity functor of is a balance on . In this way, the twist can be seen as a way of “controlling” the non-symmetric behavior of the braiding.
A braided rigid monoidal category is balanced if and only if it is a pivotal category, but a balanced monoidal category need not be rigid (cf. Selinger 2011, Lem. 4.20).
References
The original definition:
- André Joyal, Ross Street, The geometry of tensor calculus I, Adv. Math. 88 1 (1991) 55–112, [doi:10.1016/0001-8708(91)90003-P]
The above definition follows:
- Jeff Egger, Appendix C in: Of Operator Algebras and Operator Spaces (2006) [pdf]
See also:
- Peter Selinger, A survey of graphical languages for monoidal categories,
Springer Lecture Notes in Physics 813 (2011) 289-355 [arXiv:0908.3347, doi:10.1007/978-3-642-12821-9_4]
Last revised on February 21, 2024 at 05:25:13. See the history of this page for a list of all contributions to it.