nLab coordinate system
Context
Manifolds and cobordisms
manifolds and cobordisms
cobordism theory, Introduction
Definitions
Genera and invariants
Classification
Theorems
Contents
Idea
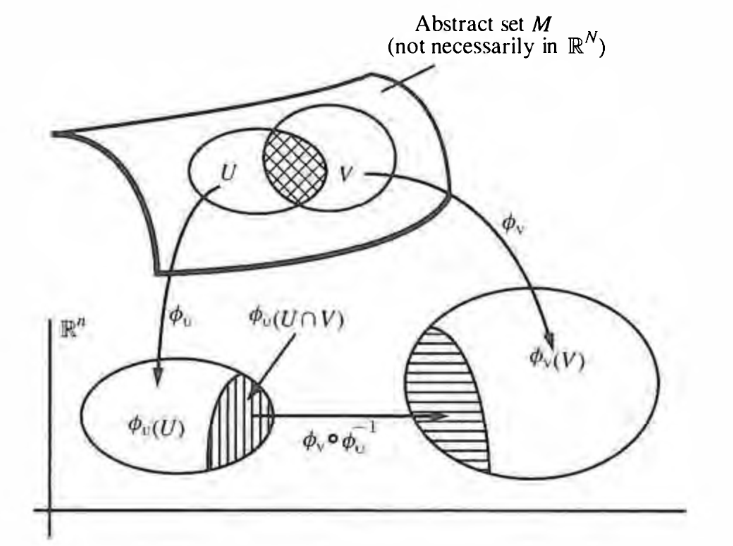
A topological manifold of dimension is by definition a topological space that is locally homeomorphic to a Cartesian space . A choice of such morphism
is a coordinate system or coordinate chart or just chart on the image of .
This generalises to other sorts of manifolds.
An atlas is the collection of coordinate charts defining a manifold structure.
graphics grabbed from Frankel
Related concepts
Last revised on August 1, 2018 at 12:04:18. See the history of this page for a list of all contributions to it.