nLab exact couple
Context
Homological algebra
(also nonabelian homological algebra)
Context
Basic definitions
Stable homotopy theory notions
Constructions
Lemmas
Homology theories
Theorems
Contents
Idea
Exact couples are a way to encode data that makes a spectral sequence, specially adapted to the case that the underlying filtering along which the spectral sequence proceeds is induced from a tower of homotopy fibers, such as a Postnikov tower or Adams tower (see also at Adams spectral sequence).
Definition
Exact couples
Definition
Given an abelian category , an exact couple in is a cyclic long exact sequence of three morphisms among two objects of the form
Remark
This being cyclic, it is usually depicted as a triangle
The archetypical example from which this and the following definition draw their meaning is example below.
Spectral sequences from exact couples
Definition
A cohomology spectral sequence is
-
a sequence , of bigraded abelian groups;
-
a sequence of differentials
such that
- is the cochain cohomology of :, i.e. .
Given a -graded abelian group_ equipped with a decreasing filtration
such that
then the spectral sequence is said to converge to , denoted,
if
-
in each bidegree the sequence eventually becomes constant on a group
;
-
is the associated graded of the filtered in that
.
The converging spectral sequence is called multiplicative if
-
is equipped with the structure of a bigraded object algebra;
-
is equipped with the structure of a filtered graded algebra ();
such that
-
each is a derivation with respect to the (induced) algebra structure on , graded of degree 1 with respect to total degree;
-
the multiplication on is compatible with that on .
Definition
(derived exact couples)
An exact couple is three homomorphisms of abelian groups of the form
such that the image of one is the kernel of the next.
Given an exact couple, then its derived exact couple is
Here and in the following we write etc. for the operation of choosing a preimage under a given function . In each case it is left implicit that the given expression is independent of which choice is made.
Proposition
(cohomological spectral sequence of an exact couple)
its derived exact couple
is itself an exact couple. Accordingly there is induced a sequence of exact couples
If the abelian groups and are equipped with bigrading such that
then with
is a cohomological spectral sequence, def. .
(As before in prop. , the notation with denotes the function given by choosing, on representatives, a preimage under , with the implicit claim that all possible choices represent the same equivalence class.)
If for every bidegree there exists such that for all
-
;
then this spectral sequence converges to the inverse limit group
filtered by
(e.g. Kochmann 96, lemma 2.6.2)
Proof
We check the claimed form of the -page:
Since in the exact couple, the kernel
consists of those elements such that , for some , hence
By assumption there is for each an such that for all then is independent of .
Moreover, consists of the image under of those such that is in the image of , hence (since by exactness of the exact couple) such that is in the kernel of , hence such that is in the kernel of . If then by assumption and so then .
(Beware this subtlety: while vanishes by the convergence assumption, the expression need not vanish yet. Only the higher power is again guaranteed to vanish. )
It follows that
where in last two steps we used once more the exactness of the exact couple.
(Notice that the above equation means in particular that the -page is a sub-group of the image of the -page under .)
The last group above is that of elements which map to zero in and where two such are identified if they agree in , hence indeed
Examples
Exact couple of a tower of (co)-fibrations
…spectral sequence of a tower of fibrations…
Definition
A filtered spectrum is a spectrum equipped with a sequence of spectra of the form
Remark
More generally a filtering on an object in (stable or not) homotopy theory is a -graded sequence such that is the homotopy colimit . But for the present purpose we stick with the simpler special case of def. .
Remark
There is no condition on the morphisms in def. . In particular, they are not required to be n-monomorphisms or n-epimorphisms for any .
On the other hand, while they are also not explicitly required to have a presentation by cofibrations or fibrations, this follows automatically: by the existence of model structures for spectra, every filtering on a spectrum is equivalent to one in which all morphisms are represented by cofibrations or by fibrations.
This means that we may think of a filtration on a spectrum in the sense of def. as equivalently being a tower of fibrations over .
The following remark unravels the structure encoded in a filtration on a spectrum, and motivates the concepts of exact couples and their spectral sequences from these.
Remark
Given a filtered spectrum as in def. , write for the homotopy cofiber of its th stage, such as to obtain the diagram
where each stage
is a homotopy fiber sequence.
To break this down into invariants, apply the stable homotopy groups-functor. This yields a diagram of -graded abelian groups of the form
Here each hook at stage extends to a long exact sequence of homotopy groups via connecting homomorphisms
If we understand the connecting homomorphism
as a morphism of degree -1, then all this information fits into one diagram of the form
where each triangle is a rolled-up incarnation of a long exact sequence of homotopy groups (and in particular is not a commuting diagram!).
If we furthermore consider the bigraded abelian groups and , then this information may further be rolled-up to a single diagram of the form
where the morphisms , and have bi-degree , and , respectively.
Here it is convenient to shift the bigrading, equivalently, by setting
because then counts the cycles of going around the triangles:
Data of this form is called an exact couple, def. below.
Definition
An unrolled exact couple (of Adams-type) is a diagram of abelian groups of the form
such that each triangle is a rolled-up long exact sequence of abelian groups of the form
The collection of this “un-rolled” data into a single diagram of abelian groups is called the corresponding exact couple.
Definition
An exact couple is a diagram (non-commuting) of abelian groups of the form
such that this is exact sequence exact in each position, hence such that the kernel of every morphism is the image of the preceding one.
The concept of exact couple so far just collects the sequences of long exact sequences given by a filtration. Next we turn to extracting information from this sequence of sequences.
Remark
The sequence of long exact sequences in remark is inter-locking, in that every appears twice:
This gives rise to the horizontal composites , as show above, and by the fact that the diagonal sequences are long exact, these are differentials: , hence give a chain complex:
We read off from the interlocking long exact sequences what these differentials mean: an element lifts to an element precisely if :
This means that the cochain cohomology of the complex produces elements of and hence of .
In order to organize this observation, notice that in terms of the exact couple of remark , the differential
is a component of the composite
Some terminology:
Definition
Given an exact couple, def. , then the induced derived exact couple is the diagram
with
-
;
-
;
-
;
-
;
-
.
Definition
Given an exact couple, def. , then the induced spectral sequence, def. , is the sequence of pages, def. , of the induced sequence of derived exact couples, def. , prop. .
Example
Consider a filtered spectrum, def. ,
and its induced exact couple of stable homotopy groups, from remark
with bigrading as shown on the right.
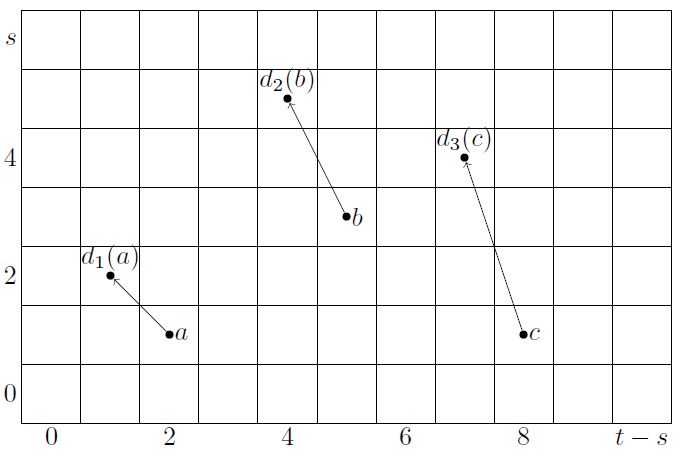
As we pass to derived exact couples, by def. , the bidegree of and is preserved, but that of increases by in each step, since
Therefore the induced spectral sequence has differentials of the form
References
The original article is
- W. S. Massey, Exact Couples in Algebraic Topology (Parts I and II), Annals of Mathematics, Second Series, Vol. 56, No. 2 (Sep., 1952), pp. 363-396 (pdf)
also
- Beno Eckmann, Peter Hilton, Exact couples in an abelian category, Journal of Algebra Volume 3, Issue 1, January 1966, Pages 38-87 (jorunal)
A class of examples leading to what later came to be known as the Atiyah-Hirzebruch spectral sequence is discussed in section XV.7 of
- Henri Cartan, Samuel Eilenberg, Homological algebra, Princeton Univ. Press (1956)
Textbook accounts include
-
Frank Adams, part III, section 7 of Stable homotopy and generalised homology, 1974
-
Stanley Kochmann, section 2.2 of Bordism, Stable Homotopy and Adams Spectral Sequences, AMS 1996
-
John McCleary, section 2.2 (from p. 37 on) in A user’s guide to spectral sequences, Cambridge University Press, 2001
-
Charles Weibel, section 5.9 An Introduction to Homological Algebra
Another review with an eye towards application to the Adams spectral sequence is in
- Doug Ravenel, chapter 2, section 1 of Complex cobordism and stable homotopy groups of spheres
Last revised on October 13, 2019 at 01:49:07. See the history of this page for a list of all contributions to it.