nLab framed link
Context
Knot theory
Examples/classes:
Types
Related concepts:
Contents
Idea
A framed link is a link where the circles forming the components are viewed as having a thickness, albeit an arbitrarily small thickness. That is to say, instead of the components of the links being embedded circles, they are embedded solid tori.
The thickening can be considered in one direction only which gives embedded ribbons. This is an equivalent definition which can be useful as it makes the distinction clearer between an embedding and the same embedding composed with, say, a Dehn twist.
A link diagram can be made into a diagram of a framed links by giving it the blackboard framing: this views each segment of the link diagram as a ribbon lying on the “blackboard”.
Definition
The precise notion of a framing on a link is perhaps most naturally given in terms of smooth structures on manifolds. We’ll start from there and later give other versions.
Framing
Let be an oriented 3-manifold, for example . The tangent bundle is a bundle with structure group which in fact admits a reduction to (invertible linear transformations with positive determinant) since is oriented. A further reduction to the structure group can be effected by a number of means, e.g., by equipping with a Riemannian metric.
Now let
be a smoothly embedded link (of oriented circles). The normal bundle of is the cokernel of the bundle inclusion
(as bundles over ); it is naturally associated with a principal -bundle. A framing of is simply a choice of section of this principal -bundle. It can be thought of as a smooth choice of unit normal vectors along points of the embedded link, and can be visualized as “ribbons”, one for each component , with one edge of the ribbon being that component.
The -bundle or circle bundle over each component can be seen as an embedded torus in . The framing itself induces a diffeomorphism on this torus which takes an element over to .
Framing number
However, it is often convenient to consider such framings, or rather their associated torus diffeomorphisms, only up to isotopy. For each component , the isotopy class is specified by an integer which gives the number of 360 degree clockwise rotations of the unit normal or clockwise twists of the ribbon as one traverses the component in the direction of its orientation. This is called the framing number.
If one regards the framed link as a ribbon link, then its framing number is the linking number of the two boundaries of the ribbon.
Thus an alternative way of describing a framing on an oriented link is by assigning an integer (framing number) to each link component.
Definition
The linking matrix of a framed link is the square matrix indexed by the connected components of the link whose off-diagonal entries are the linking numbers and whose diagonal entries are the framing numbers.
Notice that the linking matrix is a symmetric matrix.
Examples
Framings of the trefoil knot:
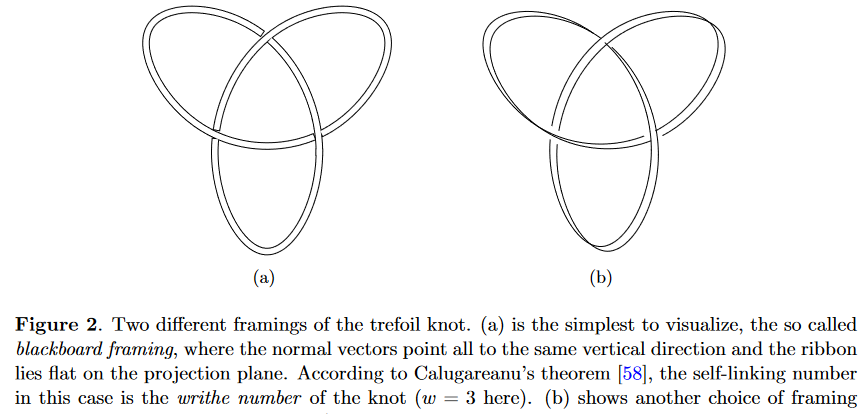
Properties
Reidemeister moves
A pair of framed link diagrams corresponds to the same framed link iff they may be deformed into each other by diagram isotopies and the following versions of the Reidemeister moves (e.g. Ohtsuki 2001 Thm. 1.8):
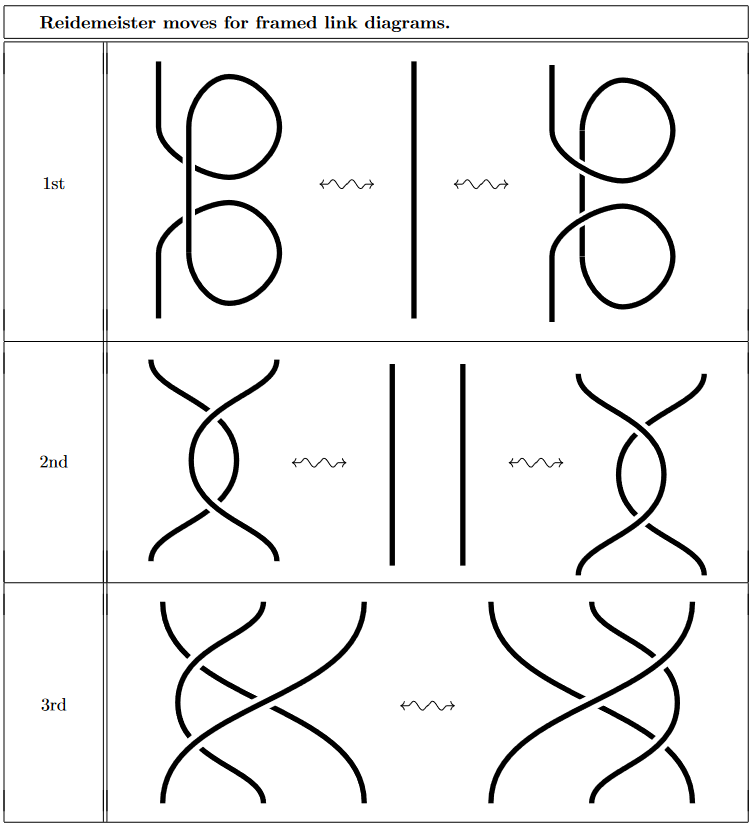
Here (only) the first is different from the 1st Reidemeister move for ordinary links: Where the latter says that a “twist” in the link diagram may by removed (by “yanking” it straight), here for framed link this is no longer the case in general, but that a twist may cancel against the opposite twist:
Related entries
References
Survey:
- Mohamed Elhamdadi, Mustafa Hajij, Kyle Istvan: Framed Knots, Math Intelligencer 42 (2020) 7–22 [doi:10.1007/s00283-020-09990-0, arXiv:1910.10257]
Textbooks:
- Tomotada Ohtsuki, pp. 15 in: Quantum Invariants – A Study of Knots, 3-Manifolds, and Their Sets, World Scientific (2001) [doi:10.1142/4746]
Lecture notes:
Vivid illustrations:
-
Mustafa Hajij: Framed knot (2022) [video:YT]
-
Nadav Drukker, Elise Paznokas, Dominik Schrimpel: Knitting Knots & the Framing Anomaly, in: Proceedings of Bridges 2022: Mathematics, Art, Music, Architecture, Culture, Tessalations Publishing (2022) 245-252 [arXiv:2210.16677, web, pdf]
Discussion of framed links in the context of regularizing Wilson loop quantum observables in Chern-Simons theory:
-
Edward Witten, pp 20 in: Quantum Field Theory and the Jones Polynomial, Commun. Math. Phys. 121 3 (1989) 351-399. MR0990772 [doi:10.1007/BF01217730,
-
Giancarlo Camilo, Dmitry Melnikov, Fábio Novaes, Andrea Prudenziati: Circuit Complexity of Knot States in Chern-Simons theory, J. High Energ. Phys. 2019 163 (2019) [arXiv:1903.10609, doi:10.1007/JHEP07(2019)163]
-
David Grabovsky: pp 22 in: Chern–Simons Theory in a Knotshell (2022) [pdf, pdf]
See also:
- Jianhua Wang: Framed and oriented links of codimension 2 [arXiv:math/0205300]
Last revised on March 20, 2025 at 15:31:59. See the history of this page for a list of all contributions to it.