nLab vine
Context
Monoidal categories
With braiding
With duals for objects
-
category with duals (list of them)
-
dualizable object (what they have)
-
ribbon category, a.k.a. tortile category
With duals for morphisms
With traces
Closed structure
Special sorts of products
Semisimplicity
Morphisms
Internal monoids
Examples
Theorems
In higher category theory
Contents
Idea
Lavers (1997) introduced the monoid of -vines, whose elements are thought of as paths between two sets of distinct points in which are allowed to merge into a single path, but not separate again. Some examples, from Lavers’ original paper, are depicted below.
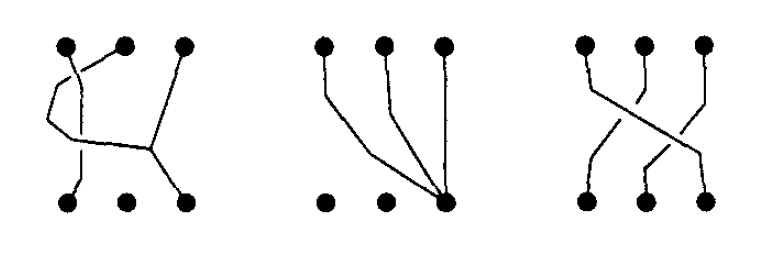
Notice that is not a group because a general vine cannot be untangled to give the trivial vine which is paths straight down. However, via pre- and post-composition, the vine monoid is acted on by the braid group on strands. When two -vines are composed any resulting strands which are only attached to one endpoint get retracted down to that endpoint, as in the following image (again from Lavers 97):
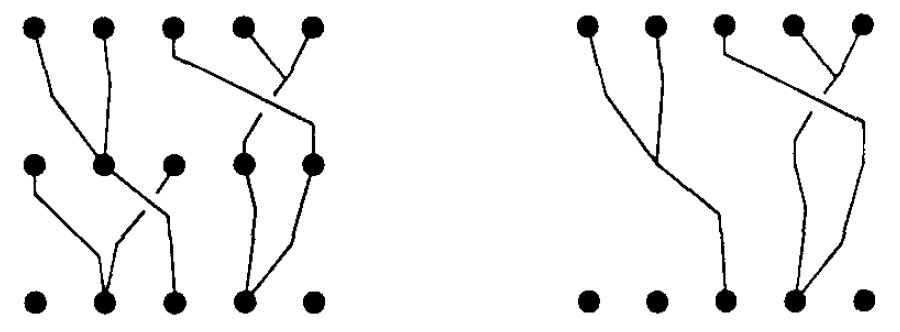
More generally, one can consider vines from points to points. As a result vines can be assembled into a category, as described below.
Definition
What is called the category of vines is the free braided strict monoidal category containing a braided monoid (i.e. an -algebra). It is also the PROB for braided monoids.
Concretely:
Definition
Let
be linearly ordered collections of points in .
Then an -vine is a set of arcs (i.e. piecewise linear maps from to ) with the following properties:
-
,
-
,
-
for all , has -coordinate ,
-
if for any then for all .
Definition
Let be the category with set of objects the natural numbers with set of morphisms being -vines modulo a suitable notion of ambient isotopy that allows arcs to be deformed up to homotopy but not pass through one another.
Properties
The monoidal structure of is given by addition of natural numbers and juxtaposition of vines. Because contains the braid category as a subcategory, it cannot be symmetric monoidal, but it is braided monoidal. The braiding is the same as that of the braid category, the “-over-” braid depicted below.
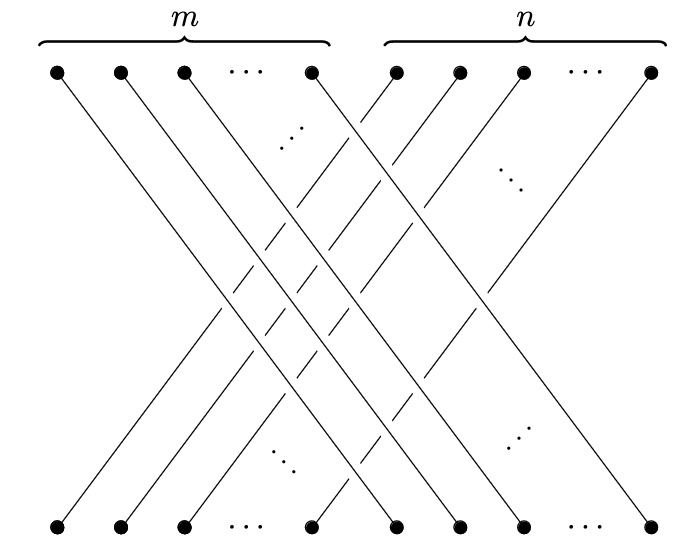
Exercise
Show that the above is a braided monoidal structure on .
References
-
T. G. Lavers, The theory of vines, Comm. Algebra 25 4 (1997) 1257–1284 [doi:10.1080/00927879708825919]
-
Mark Weber, §6.3 of: Internal algebra classifiers as codescent objects of crossed internal categories. Theory and Applications of Categories, 30 50 (2015) 1713–1792 [tac:30/50, pdf]
Last revised on February 13, 2024 at 10:17:07. See the history of this page for a list of all contributions to it.