nLab weak gravity conjecture
Context
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Contents
Idea
The weak gravity conjecture is a conjecture (Arkani-Hamed, Motl, Nicolis, Vafa 06) often summarized as saying that for gravity or quantum gravity to be consistent, the force of the field of gravity must be weaker than that of any of the gauge field forces, in suitable units.
Loose statement
More precisely, what is argued in (AH-M-N-V 06, section 2) is that there alwayst must be “elementary particles” for which the ratio of their mass over their gauge field charge (e.g. electric charge, magnetic charge) is smaller than one: (in natural units).
The argument for this in (AH-M-N-V 06, section 2.2) is the following. The extremal (BPS state) bound for charged black holes is that their mass exceeds or equals their charge , hence . Now via black hole radiation any black hole is supposed to eventually decay by radiating away elementary particle quanta. If there were no elementary particle with , so the argument goes, then by radiating away particles with the black hole would eventually lose all its mass, while still having some non-vanishing charge left. But such “black hole remnants” have been argued to lead to inconsistency (Susskind 96).
In string theory
The weak gravity conjecture was originally motivated from string theory, which is argued to validate the “weak gravity” assumption.
In (AH-M-N-V 06, section 4) it is argued that the closed superstring excitation states in heterotic string theory KK-compactified on to 4d satisfy the condition :
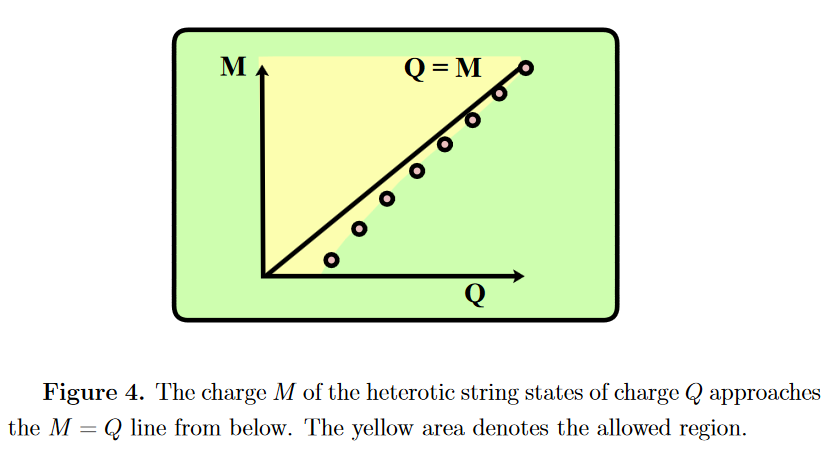
Relation to cosmic censorship
In 2015 Cumrun Vafa has argued that the weak gravity conjecture implies the cosmic censorship hypothesis: The latter turns out to be generally false, even in in 4 dimensions (Crisford-Santos 17), but there are arguments that configurations violating it also violate the assumption of “weak gravity”.
Subsequent calculations by Santos and Crisford supported Vafa’s hunch; the simulations they’re running now could verify that naked singularities become cloaked in black holes right at the point where gravity becomes the weakest force. (Wolchover, June 20 2017)
For more on this see Horowitz-Santos 19
Related concepts
References
The statement is due to
- Nima Arkani-Hamed, Lubos Motl, Alberto Nicolis, Cumrun Vafa, The String Landscape, Black Holes and Gravity as the Weakest Force, JHEP 0706:060,2007 (arXiv:hep-th/0601001)
with reference to arguments in
- Leonard Susskind, Trouble For Remnants (arXiv:hep-th/9501106)
Review:
-
Eran Palti: The Swampland: Introduction and Review, lecture notes [arXiv:1903.06239]
-
Tom Rudelius: An Introduction to the Weak Gravity Conjecture [arXiv:2409.02161]
Further discussion includes
-
Clifford Cheung, Grant N. Remmen: Naturalness and the Weak Gravity Conjecture, Phys. Rev. Lett. 113 051601 (2014) [arXiv:1402.2287, doi:10.1103/PhysRevLett.113.051601]
-
Yu Nakayama, Yasunori Nomura, Weak Gravity Conjecture in AdS/CFT, Phys. Rev. D 92, 126006 (2015) (arXiv:1509.01647)
-
Ben Heidenreich, Matthew Reece, Tom Rudelius, Sharpening the Weak Gravity Conjecture with Dimensional Reduction, JHEP02(2016)140 (arXiv:1509.06374)
-
Clifford Cheung, Junyu Liu, Grant N. Remmen: Proof of the Weak Gravity Conjecture from Black Hole Entropy [arXiv:1801.08546, doi:10.1007/JHEP10(2018)004]
-
Miguel Montero, A Holographic Derivation of the Weak Gravity Conjecture, JHEP 03 (2019) 157 (arXiv:1812.03978)
-
Ben Heidenreich, Matthew Reece, Tom Rudelius, Repulsive Forces and the Weak Gravity Conjecture (arXiv:1906.02206)
Relation to cosmic censorship hypothesis
-
Toby Crisford, Jorge Santos, Violating weak cosmic censorship in AdS, Phys. Rev. Lett. 118, 181101 (2017) (arXiv:1702.05490)
-
Gary Horowitz, Jorge Santos, Further evidence for the weak gravity - cosmic censorship connection (arXiv:1901.11096)
Relation, via AdS/CFT and the conformal bootstrap, to the solution of the sphere packing problem in dimensions 8 and 24:
- Thomas Hartman, Dalimil Mazáč, Leonardo Rastelli, Sphere Packing and Quantum Gravity (arXiv:1905.01319)
See also:
- Lars Aalsma, Alex Cole, Gregory J. Loges, Gary Shiu, A New Spin on the Weak Gravity Conjecture (arXiv:2011.05337)
Proof of the weak gravity conjecture in bosonic string theory is claimed in:
- Ben Heidenreich, Matteo Lotito, Proving the Weak Gravity Conjecture in Perturbative String Theory, Part I: The Bosonic String [arXiv:2401.14449]
See also:
- Yong Xiao, Qiang Wang, Aonan Zhang: A Proof of the Weak Gravity Conjecture via Leading-Order Quantum Gravity Effects [arXiv:2503.08459]
In relation to positivity relations among scattering amplitudes:
- Tran Quang Loc: Exploring amplitude criteria for weak gravity in electroweak theory [arXiv:2505.01497]
Last revised on May 6, 2025 at 06:31:38. See the history of this page for a list of all contributions to it.