nLab super-Cartan geometry
Context
Super-Geometry
superalgebra and (synthetic ) supergeometry
Background
Introductions
Superalgebra
Supergeometry
Supersymmetry
Supersymmetric field theory
Applications
Gravity
Formalism
Definition
Spacetime configurations
Properties
Spacetimes
| black hole spacetimes | vanishing angular momentum | positive angular momentum |
|---|---|---|
| vanishing charge | Schwarzschild spacetime | Kerr spacetime |
| positive charge | Reissner-Nordstrom spacetime | Kerr-Newman spacetime |
Quantum theory
Contents
- Idea
- Survey of (non-)existing literature
- Introduction
- 1) The geometric substance
- Coordinate systems: super Cartesian spaces
- The geometric determinations
- Principal bundles and Higher geometry
- 2) General Cartan geometry
- 3) Super-Cartan geometry for Supergravity
- Super differential forms
- Super Lie algebra valued super differential forms
- Supersymmetry and Super-Minkowski spacetime
- Poincaré connections: Graviton and gravitino field
- Cohomology of super-Minkowski spacetime
- The Brane molecule
- Related entries
- References
Idea
While Cartan geometry was originally conceived of in the context of differential geometry, its principles and constructions make sense much more generally. In particular they make sense in the context of supergeometry. The implementation of Cartan geometry in supergeometry may well be called super-Cartan geometry or Cartan super-geometry. Where the original and motivating example for plain Cartan geometry was the formulation of Einstein gravity (via pseudo-Riemannian geometry), so super-Cartan geometry underlies and finds motivation from the formulation of supergravity, see also the Survey of (non-)existing literature below.
While the abstract general theory of super-Cartan geometry proceeds in direct analogy with that of traditional Cartan geometry, the concrete particular examples tend to exhibit a richer behaviour. Specifically for the case relevant to supergravity this is due to two facts:
-
The super Euclidean spaces and super-Minkowski spacetimes, have, as super-translation groups, non-abelian supergroup structure, which is reflected in the fact that the left-invariant 1-forms (super differential forms) on these spaces are not closed. This means that they carry natural intrinsic torsion of a G-structure. Due to this fact the super-Cartan geometry involved in supergravity is richer than its bosonic counterpart in a way that goes beyond the addition of “superpartners”. For more on this see also at torsion constraints of supergravity.
-
In particular super-Minkowski spacetimes carry non-trivial exceptional super Lie algebra cocycles. Their globalization as definite forms is hence analogous to what is known in the bosonic case for instance for G₂-structure. These globalizations play a key role in the discussion of super p-brane sigma-models on curved supergravity backgrounds. Moreover, these cocycles classify super L-infinity algebra extensions of super Minkowski spacetime known as extended super Minkowski spacetimes. This is the origin of much of higher Cartan geometry within super-Cartan geometry.
Survey of (non-)existing literature
While the specific terminology “super-Cartan geometry” is traditionally not used much (but see Baaklini 1977a, 1977b; Egeileh & Chami 2013), nevertheless the key ingredients of super-Cartan geometry are well known in the literature, and all the more is it useful to make them explicit as what they are.
Physics literature usually refers to the “superspace formulation” of supergravity when referring to the formulation of the theory in supergeometry and uses terms such as “Einstein-Cartan theory” to refer to the first order formulation of gravity (e.g. Nieuwenhuizen 81). But all of the literature on supergravity formulated this way in “superspace” is implicitly about super-Cartan geometry for the inclusion of a spin group-double cover of the Lorentz group inside a super Poincaré group, in direct analogy to how ordinary Einstein gravity (pseudo-Riemannian geometry) is the Cartan geometry of the inclusion of a Lorentz group inside a plain Poincaré group – this in fact being Cartan’s original and motivating example for the whole theory. Where physicists speak of “locally gauging supersymmetry” the mathematical formulation of that is precisely this: the “supersymmetry” supergroup is the super Poincaré group acting on super Minkowski spacetime, and “locally gauging” it means exactly to consider spacetimes that are locally (tangent space-wise) modeled on super Minkowski space, while globally varying according to a Lorentz group-G-structure, hence the super-analog of a pseudo-Riemannian metric. The main point to be aware of is that physics literature in general tends to by default outright ignore all global issues (such as nontrivial principal bundles) and instead discuss these only when absolutely necessary as extra phenomena going by names such as instantons and anomalies.
With this understood, one physics references which explores the super-Cartan-geometric picture of supergravity in much detail is (D’Auria-Fre 82, Castellani-D’Auria-Fre 91). (In part I These authors speak of ‘Poincaré gravity’. In part II they make even the higher Cartan geometry hidden here fairly explicit, see there and see at D'Auria-Fré formulation of supergravity). Similarly, discussion of super-Klein geometry in the context of supergravity is, even if not exactly in this terminology, rather explicit in (Figueroa-O’Farrill 08).
An early reference that identifies this first order formulation of gravity explicitly as a Cartan connection is (Baaklini 77a, Baaklini 77b), which however seems to have gone unnoticed. (The only non-self citation to this article is in the list of references of the survey (Nieuwenhuizen 81) which however does not actually refer the article in its text.) A much later reference that very clearly identifies the role of the mathematics of supergeometric G-structures (which is the relevant special class of super-Cartan geometry) in supergravity in the context of supergravity torsion constraints is (Lott 01). The followup (Egeileh-Chami 13) to that article again makes the terminology “Cartan geometry” fully explicit in this supergeometric context. This last article also observes that from this perspective the traditional concept of Killing spinor – which involves an extra “weakening” parameter in addition to the plain concept of a covariantly constant spinor – is naturally understood as being in fact a covariantly constant spinor, but for a different model super-Klein geometry .
This provides ample example and application of super-Cartan geometry for the case where is a super vector space, hence for the case corresponding to G-structure. More general super-Cartan geometry apparently remains to be explored.
Introduction
It is traditional to introduce supergeometry as being about supermanifolds and to introduce the concept of supermanifolds in the form of locally ringed topological spaces. There is however a more direct, possibly more illuminating, and certainly more powerful way, following instead the spirit of the discussion at geometry of physics – smooth sets.
Below in
we consider the full topos of supergeometry and find how its structure reflects the special qualities of supergeometry.
Then in
we discuss how to formulate manifolds and their Cartan geometry generally in such a context. Finally in
we put this together and discuss supermanifolds equipped with super Cartan geometry.
1) The geometric substance
Coordinate systems: super Cartesian spaces
Recall the following from the discussion at geometry of physics – smooth sets. We will set up supergeometry in direct analogy to this formulation of plain differential geometry. See also at geometry of physics – manifolds and orbifolds and geometry of physics – supergeometry.
Definition
Write CartSp for the category of Cartesian space for with smooth functions between them. Say that a collection of morphisms in is covering if this is a good open cover in that every finite non-empty intersection of the charts is diffeomorphic to a Cartesian space.
Remark
We may think of this as the category of abstract coordinate systems on which differential geometry is to be modeled, see at geometry of physics – coordinate systems.
Definition
We say a smooth set or smooth 0-type is a sheaf on , write
for the sheaf topos of all these.
Remark
The useful way to think of def. in the present context is as defining a kind of generalized smooth space which is defined by which smooth functions from Cartesian spaces it receives (see also at motivation for sheaves, cohomology and higher stacks for more exposition of this point).
Under the Yoneda embedding
every Cartesian space is naturally regarded as a smooth space itself, namely the one it represents by the assignment
Hence the set that the Cartesian space , regarded as a sheaf, assigns to a coordinate system is just the set of all ways of mapping that coordinate system smoothly into .
Hence given any , we are entitled to think of it as a generalized smooth space which need not be given as a set equipped with smooth structure, but whose nature instead we detect or probe by mapping Cartesian spaces into it: given then we think of the set , which the sheaf assigns, as playing the role of the set of all smooth functions “” into the would-be space .
The Yoneda lemma gives that this is not circular, but consistent: once we identify Cartesian spaces themselves as smooth spaces via the Yoneda embedding, then the previous statement becomes literally true and we may remove the quotation marks:
Remark
The strategy is then to work with this nice category (a topos) of smooth spaces, and find in their subcategories of more specific objects having extra properties which one may need in given applications:
coordinate systems smooth manifolds Hilbert manifolds Banach manifolds Fréchet manifolds diffeological spaces smooth spaces smooth orbifolds smooth groupoids smooth 2-groupoids smooth ∞-groupoids
The identification of (super-)smooth manifolds inside all (super-)smooth spaces we consider below.
In view of the above, it is immediate that in order to generalize differential geometry, we should focus on generalizing the category of coordinate systems. To that end recall a basic fact about smooth functions:
Proposition
The functor
which sends a Cartesian space to (the formal dual of) its -algebra of smooth functions is a full and faithful functor.
In other words, for two Cartesian spaces there is a natural bijection between the smooth functions and the algebra homomorphisms .
See at embedding of smooth manifolds into formal duals of R-algebras for more on this.
Remark
One has to be careful that prop. might seem to imply more than it does. In order that all constructions on all commutative algebras have the desired dual effect on formally dual smooth spaces (e.g. construction of products/coproducts, or construction of Kähler differentials) one needs to refine plain commutative algebras over to smooth algebras. See there for more on this point, which however for our purposes here is not of further concern.
Now to pass to superalgebra:
Remark
It is an observation from experiment (from the Stern-Gerlach experiment via the spin-statistics theorem), that spaces of physical fields for physical theories that contain fermions behave as if they have algebras of functions which are not quite commutative algebras, but where the functions depending on the fermions only commute with each other up to picking up a minus sign.
Definition
A super-commutative superalgebra (or just commutative superalgebra for short) is a -graded associative algebra such that for any two elements in homogeneous degree , then their product is related by (Grassmann 1844, §37, §55)
Write for the category of commutative superalgebras over .
Definition
For , the real Grassmann algebra
is the -algebra freely generated from generators subject to the relation
For , the super-Cartesian space is the formal dual of the commutative superalgebra written whose underlying -graded vector space is
with the product given by the relations
where is the ordinary pointwise product of smooth functions.
Write
for the full subcategory of the opposite category of commutative superalgebras on those of this form. We write for the formal dual of .
Definition
Say that a collection of morphisms in is covering if all and the are (for the same and ), the morphisms are the identity on the odd generators , and the underlying map of Cartesian spaces is a good open cover in the sense of def. . Write
for the sheaf topos over that site. We call this the collection of smooth super spaces.
This is the topos that hosts traditional supergeometry. However for our purposes it is useful to refine this a little more to a context for synthetic differential supergeometry. To that end first observe that
Remark
The even-degree part is an ordinary commutative algebra, but if then it is not the algebra of functions on any smooth manifold, because it has a non-trivial nilpotent ideal. Instead, a nilpotent element of an algebra of functions may be thought of as a function depending on an infinitesimal direction.
For instance is isomorphic to what is known as the algebra of dual numbers with .
This is traditionally more familiar from the theory of formal schemes, but the same kind of general abstract theory goes through in the context of differential geometry, a point of view known as synthetic differential geometry.
But this means that in passing to commutative superalgebras there are two stages of generalizations of plain differential geometry involved:
-
smooth manifolds are generalized to formal smooth manifolds;
-
formal smooth manifolds are further generalized to formal smooth supermanifolds.
It will be useful to make this explicit.
Definition
Write
for the full subcategory of the opposite category of commutative algebras over on formal duals of commutative algebras over the real numbers of the form with a finite-dimensional nilpotent ideal. We call this the category of infinitesimally thickened points.
Write moreover
for the full subcategory on formal duals of those algebras which are tensor products of commutative -algebras of the form
of algebras of smooth functions as in def. with algebras corresponding to infinitesimally thickened points as above.
The sheaf topos
is traditionally known as the Cahiers topos.
Example
Write for the formal dual of the algebra of dual numbers. Then morphisms
which are the identity after restriction along , are equivalently algebra homomorphisms of the form
which are the identity modulo . Such a morphism has to take any function to
for some smooth function . The condition that this assignment makes an algebra homomorphism is equivalent to the statement that for all
Multiplying this out and using that this in turn is equivalent to
This in turn means equivalently that is a derivation. But derivations of algebras of smooth functions are equivalent to vector fields. (See at derivations of smooth functions are vector fields).
In particular one finds that maps
are equivalently single tangent vectors.
Definition
Write
for the full subcategory on those formal duals of commutative superalgebras over the real numbers on those of the form with a finite dimensional nilpotent ideal.
We call this the category of infinitesimally thickened superpoints.
Similarly write
for the full subcategory on formal duals of tensor products of an algebra of smooth functions and an algebra on an infinitesimally thickened superpoint.
The sheaf topos
we call that of super formal smooth spaces.
The geometric determinations
The sites considered above are related by a sequence of reflections and coreflections as follows
Definition
Write
for the evident full inclusions:
-
the first one picks the terminal object ;
-
the second one regards as a formal manifold equipped with no infinitesimal thickening;
-
the third one regards as a supergeometric space with no odd-graded (no fermionic) component.
Remark
The sites in question are alternatingly (co-)reflective subcategories of each other (we always display left adjoints above their right adjoints)
Here
-
the first inclusion picks the terminal object ;
-
the second inclusion is that of reduced objects; the coreflection is reduction, sending an algebra to its reduced algebra;
-
the third inclusion is that of even-graded algebras, the reflection sends a -graded algebra to its even-graded part, the co-reflection sends a -graded algebra to its quotient by the ideal generated by its odd part, see at superalgebra – Adjoints to the inclusion of plain algebras.
Proposition
Passing to (∞,1)-categories of (∞,1)-sheaves, this yields, via (∞,1)-Kan extension, a sequence of adjoint quadruples as follows:
Passing to the adjoint triples of idempotent monads and idempotent comonads which this induces, then yields
-
on the left the shape modality , flat modality and sharp modality ,
-
in the middle yields the reduction modality , the infinitesimal shape modality and the infinitesimal flat modality .
-
on the right we get an adjoint triple whose whose middle bit is the bosonic modality and whose left piece produces super-even components, containing all the “fermion conserved currents” if one wishes , which in this unity of opposites hence deserves to be called the fermionic modality. The further right adjoint is the rheonomy modality.
Hence we get a progression of adjoint modalities of the form
where “” denotes inclusion of modal types. The first level is cohesion, the second is differential cohesion (elasticity), the third is a further refinement given by supergeometry, which takes further “square roots” of all infinitesimal generators.
Proof
All the sites are ∞-cohesive sites, which gives that we have an cohesive (infinity,1)-topos. The composite inclusion on the right is an ∞-cohesive neighbourhood site, whence the inclusion exhibits differential cohesion.
With this the rightmost adjoint quadruple gives the Aufhebung of by and the further opposition .
For convenience, from now on we notationally abbreviate:
Remark
induces an idempotent monad on , i.e. an endofunctor
equipped with a natural transformation
such that applying again to that transformation it becomes an isomorphism.
Dually, any coreflective subcategory
induces an idempotent comonad
If moreover these two cases combine to an adjoint triple of the form
or of the form
then these (co-)monads themselves are adjoint to each other as
or as
respectively, forming an “adjoint cylinder”.
Notice the following:
Proposition
The total composite labeled in prop. is indeed the locally constant sheaf-functor for .
Proof
Let be any object in image of this total functor, and let . Then by adjunction is equivalently homs in out of the dual of the Weil algebra which is the quotient of the original one by the ideal generated by its odd part. Hence this, in turn, is equivalently homs in out of and that finally is equivalently homs in out of into the given set.
Corollary
Passing, via remark , from the sequence of adjoint quadruples in prop. , yields the following system of adjoint triples of idempotent monads and idempotent comonads:
where denotes inclusion of modal types.
We pronounce the operations in corollary as follows.
-
-
fermionic modality – the spaces it sends to the point are purely fermionic, the odd line;
-
bosonic modality – sends a super-space to the underlying bosonic space;
-
-
-
reduction modality – removes infinitesimal thickening;
-
infinitesimal shape modality – sends a space to its de Rham space;
-
-
-
shape modality – sends a space to its set of connected components; or rather, once we lift the discussion here from sheaves to infinity-stacks, then this sends a space to its fundamental infinity-groupoid;
-
flat modality – sends a space to the discrete space formed by its points;
-
Example
-
For any ordinary smooth manifold, this is a bosonic modal type .
-
The odd line is purely fermionic in that it is an -comodal type: .
-
All super Cartesian spaces have contractible shape in that .
By applying universal constructions to the units/counits of these modalities, we obtain various further operations that will be useful
Definition
Given , its infinitesimal disk bundle is the pullback of the unit of the infinitesimal shape modality along itself
Given a point , then the infinitesimal neighbourhood of that point is the further pullback of the infinitesimal disk bundle to this point:
Remark
This is the input for the formulation of frame bundles below around prop. .
It is natural not to pick any point, but to collect all infinitesimal disks around all the points of a space:
Definition
The relative shape modality is the operation that sends to the homotopy pullback
There are some further relations between the modalities to take note of:
Proposition
We have the following Aufhebung-relations:
-
(the codiscrete objects form a dense subtopos)
-
.
Proof
For any and any we have by adjunction natural equivalences
Principal bundles and Higher geometry
The point of the system of modalities in corollary is that they allow to carry various geometric theory across different models of geometry. If we formulate traditional Cartan geometry in with just these operations, then we may just carry that verbatim to to get a theory of super-Cartan geometry. This we get to below.
In the same vein, we may increase the in to and get higher Cartan geometry.
In fact at least is necessary in order to formalize frame bundles via their modulating morphisms to the delooping . The case is obtained by replacing in the above sheaves of sets with stacks of groupoids. The case is obtained by further refining this to infinity-stacks of infinity-groupoids.
Here we just recall some bare minimum of this higher differential geometry, for formulating Cartan geometry we need to speak of frame bundles and hence here we mainly need the concept of principal infinity-bundle, for more see at geometry of physics – principal bundles.
Proposition
The (infinity,1)-category theory analog of prop. still holds, and produces via the direct analog corollary a system of modal operators on SuperFormalSmooth∞Type.
Proposition
For a group object (∞-group), the -principal bundles on any are equivalent to morphisms into the delooping object of , the equivalence being established by sending such a morphism to its homotopy fiber
2) General Cartan geometry
Given a topos of differential cohesion as in corollary above (hence an elastic substance), then on general abstract grounds there is – and that’s the point of this axiomatic formulation – a good concept and theory of V-manifolds and G-structures on these. Applied to the case of supergeometry as established in prop. this hence yields a theory of -structures on V-manifold in supergeometry, and hence of Cartan geometry modeled on the inclusion . Here we recall the elements of abstract general Cartan geometry formulated axiomatically this way. Below in Super Cartan geometry we then specify to the concrete particular super Cartan geometry.
-Manifolds
See also at geometry of physics – manifolds and orbifolds.
Definition
Given then a morphism is a local diffeomorphism if its naturality square of the infinitesimal shape modality
is a pullback square.
Remark
The abstract definition comes down to being the appropriate synthetic differential supergeometry-version of the traditional statement that is a local diffeomorphism if the diagram of tangent bundles
To see this, notice by the discussion at synthetic differential geometry that for an infinitesimally thickened point, then for any the mapping space is the jet bundle of with jets of order as encoded by the infinitesimal order of . In particular if is the first order infinitesimal interval defined by the fact that its algebra of functions is the algebra of dual numbers , and is a smooth manifold, then
is the ordinary tangent bundle of . Now use that the internal hom preserves limits in its second argument, and that, by the hom-adjunction, and finally use that .
Let now be given, equipped with the structure of a group (infinity-group).
Definition
A V-manifold is an such that there exists a -atlas, namely a correspondence of the form
with both morphisms being local diffeomorphisms, def. , and the right one in addition being an epimorphism, hence an atlas.
Proposition
If is a local diffeomorphism, def. , then so is its image under the bosonic modality.
Proof
Since the bosonic modality provides Aufhebung for by prop. we have . Moreover anyway. Finally preserves pullbacks (being in particular a right adjoint). Hence hitting a pullback diagram
with yields a pullback diagram
Frame bundles
Definition
The general linear group is the automorphism infinity-group of the infinitesimal neighbourhood , def. , of the neutral element :
Proposition
For a -manifold, def. , then its infinitesimal disk bundle , def. , is associated to a -principal – to be called the frame bundle, modulated by a map to be called , producing homotopy pullbacks of the form
Definition
A framing of a -manifold is a trivialization of its frame bundle, prop. , hence a diagram in of the form
Remark
It is useful to express def. in terms of the slice topos . Write for the canonical morphism regarded as an object in the slice. Then a framing as in def. is equivalently a morphism
in .
Proposition
The group object , canonically regarded as a -manifold, carries a canonical framing, def. , , induced by left translation.
-Structure
See also at geometry of physics – G-structure and Cartan geometry.
Definition
Given a homomorphism of groups , a G-structure on a -manifold is a lift of the frame bundle of prop. through this map
Remark
As in remark , it is useful to express def. in terms of the slice topos . Write for the given map regarded as an object in the slice. Then a -structure according to def. is equivalently a choice of morphism in of the form
In other words, is the moduli stack for -structures.
Example
A choice of framing , def. , on a -manifold induces a G-structure for any , given by the pasting diagram in
or equivalently, via remark and remark , given as the composition
We call this the left invariant -structure.
Definition
For a -manifold, then a G-structure on , def. , is integrable if for any -atlas the pullback of the -structure on to is equivalent there to the left-inavariant -structure on of example , i.e. if we have an correspondence in the double slice topos of the form
The -structure is infintesimally integrable if this holds true at at after restriction along the relative shape modality , def. , to all the infinitesimal disks in :
Definition
Consider an infinity-action of on which linearizes to the canonical -action on by def. . Form the semidirect product . Consider any group homomorphism .
A -Cartan geometry is a -manifold equipped with a -structure, def. . The Cartan geometry is called (infinitesimally) integrable if the -structure is so, according to def. .
Remark
For an abelian group, then in traditional contexts the infinitesimal integrability of def. comes down to the torsion of a G-structure vanishing. But for a nonabelian group, this definition instead enforces that the torsion is on each infinitesimal disk the intrinsic left-invariant torsion of itself.
Traditionally this is rarely considered, matching the fact that ordinary vector spaces, regarded as translation groups , are abelian groups. But super vector spaces regarded (in suitable dimension) as super translation groups are nonabelian groups (we discuss this in detail below in The super-Klein geometry: super-Minkowski spacetime). Therefore super-vector spaces may carry intrinsic torsion, and therefore first-order integrable -structures on -manifolds are torsion-ful.
Indeed, this is a phenomenon known as the torsion constraints in supergravity. Curiously, as discussed there, for the case of 11-dimensional supergravity the equations of motion of the gravity theory are equivalent to the super-Cartan geometry satisfying this torsion constraint. This way super-Cartan geometry gives a direct general abstract route right into the heart of M-theory.
This we come to now in Super-Cartan geometry for Supergravity.
3) Super-Cartan geometry for Supergravity
Above in The geometric substance we have prepared a topos context for supergeometry with a system of modal operators that accurately reflect the three levels of geometric structure in supergeometry: smooth structure, infinitesimal thickening and fermionic odd grading.
Then in G-Structure and Cartan geometry we have used these modal operators to formulate Cartan geometry on -manifolds, def. , for any given local model group space .
Here we now consider a concrete particular choice for such a : super-Minkowski spacetimes.
Super differential forms
A super Cartesian space is the formal dual of the commutative superalgebra
in that a smooth function is equivalently (by definition!) a superalgebra homomorphism
Notice then that from knowledge of an algebra of functions one obtains the corresponding de Rham complex by the idea of Kähler differentials. As discussed there, this statement requires a little care in the smooth context, but the result is still immediate:
For a Cartesian space, then its de Rham complex is the -graded commutative dg-algebra whose underlying -graded vector space is
and whose differential is defined in degree-0 by
and extended from there to all degree by the graded Leibnitz rule.
It is immediate to generalize this to the super-context, one just needs to be sure to apply the sign rule throughout.
Definition
The de Rham complex of super differential forms on a super Cartesian space is the -bigraded commutative algebra
whose differential is defined in degree-0 by
and extended from there to all degree by the graded Leibnitz rule.
Remark
We may write
for elements in this bigrading group.
In this notation the grading of the elements in is all induced by the fact that the de Rham differential itself is a derivation of degree .
| generator | bi-degree |
|---|---|
| (0,even) | |
| (0,odd) | |
| (1,even) |
Here the last line means that we have
| generator | bi-degree |
|---|---|
| (0,even) | |
| (0,odd) | |
| (1,even) | |
| (1,odd) |
The formula for the “cohomologically- and super-graded commutativity” in is
for all of homogeneous -degree. Hence there are two contributions to the sign picked up when exchanging two super-differential forms in the wedge product:
-
there is a “cohomological sign” which for commuting a -forms past an -form is ;
-
in addition there is a “super-grading” sich which for commuting a -graded coordinate function past a -graded coordinate function (possibly under the de Rham differential) is .
Example
See at signs in supergeometry for further discussion, for literature, and for mentioning of another popular sign convention, which is different but in the end yields the same cohomology.
Super Lie algebra valued super differential forms
We want to discuss the generalization of the concept of Lie algebra valued differential forms from ordinary differential geometry to supergeometry. To that end, we first recall the following neat formulation of ordinary Lie algebra valued differential forms due to Cartan. This will lend itself in fact not only to the generalization to super Lie algebras but further to super L-∞ algebras, which is what is needed for the desciption of higher dimensional supergravity.
Definition
The Chevalley-Eilenberg algebra of a finite dimensional Lie algebra is the semifree graded-commutative dg-algebra whose underlying graded algebra is the Grassmann algebra
(with the th skew-symmetrized power in degree )
and whose differential (of degree +1) is on the dual of the Lie bracket
extended uniquely as a graded derivation on .
That this differential indeed squares to 0, , is precisely the fact that the Lie bracket satisfies the Jacobi identity.
Remark
If in the situation of prop. we choose a dual basis of and let be the structure constants of the Lie bracket in that basis, then the action of the differential on the basis generators is
where here and in the following a sum over repeated indices is implicit.
Proposition
The construction of Chevalley-Eilenberg algebras in def. yields a fully faithful functor
embedding Lie algebras into formal duals of differential graded algebras. Its image consists of precisely of the semifree dg-algebras, those whose underlying graded algebra (forgetting the differential) is a Grassmann algebra generated on a vector space.
Definition
Given a Lie algebra , its Weil algebra is the semi-free dga whose underlying graded-commutative algebra is the exterior algebra
on and a shifted copy of , and whose differential is the sum
of two graded derivations of degree +1 defined by
-
acts by degree shift on elements in and by 0 on elements of ;
-
acts on unshifted elements in as the differential of the Chevalley-Eilenberg algebra of and is extended uniquely to shifted generators by graded-commutattivity
with :
for all .
Proposition
Given a Lie algebra , then a Lie algebra valued differential form on, say, a Cartesian space , is equivalently a dg-algebra homomorphims
hence there is a natural bijection
The form is flat in that its curvature differential 2-form vanishes, precisely if this morphism factors through the CE-algebra.
Remark
With a choice of basis as in remark , then the content of prop. is seen in components as follows:
a dg-algebra homomorphism is first of all a homomorphism of graded algebras, and since the domain is free as a graded algebra, such is entirely determined by what it does to the generators
But being a dg-algebra homomorphism, this assignment needs to respect the differentials on both sides. For the original generators this gives
With this satisfied, then, by the very nature of the Weil algebra, the differential is automatically respected also on the shifted generators. This statement is the Bianchi identity.
Now to pass this to superalgebra.
Definition
For a super vector space, then its Grassmann algebra is the free -bigraded commutative algebra subject to
In the spirit of prop. we may then simply say that:
Definition
A super Lie algebra structure on a super vector space is the formal dual of a -bigraded commutative differential algebra
(with differential of degree (1,even)) such that the underlying graded algebra is the super Grassmann algebra via def. .
We call this again the Chevalley-Eilenberg algebra of the super Lie algebra dually defined thereby.
Similarly, the Weil algebra is obtained from this by adding a generator in degree for each previous generator in degree and extending the differential as in def. .
Unwinding what this means, one finds that it is equivalent to the following more traditional definition:
Proposition
A super Lie algebra is equivalently
-
equipped with a bilinear bracket
which is graded skew-symmetric: it is skew symmetric on and symmetric on .
-
that satisfied the -graded Jacobi identity in that for any three elements of homogeneous super-degree then
But with def. we immediately known, in view of prop. , what super Lie algebra valued super differential forms should be:
Definition
Given a super Lie algebra , def. , prop. , then a -valued super-differential form on the super Cartesian space is a -graded dg-algebra homomorphism
from the Weil algebra according to def. , to the super de Rham complex of def. .
Accordingly we write
Example
Let be the ordinary abelian line Lie algebra. Then
is the set of super-differential forms in degree .
Similarly with the odd line regarded as an abelian super Lie algebra, then
So generally for an ordinary Lie algebra regarded as a super Lie algebra, then is bigger than .
This is an issue to be dealt with when describing supergravity in terms of Cartan fields on supermanifolds , because the actual spacetime manifold one cares about is just the bosonic part . This issue is deal with by the concept of rheonomy.
Supersymmetry and Super-Minkowski spacetime
We consider now very specific super Lie algebras, def. , those of supersymmetry.
Just as traditional Cartan geometry involves a pair of Lie algebras , so super-Cartan geometry involves a similar pair of super Lie algebras. For describing supergravity, we now want to establish an superalgebra-analog of the inclusion of the Lorentz Lie algebra into the Poincaré Lie algebra .
| (higher-)Cartan geometry | |||
|---|---|---|---|
| Einstein gravity | |||
| supergravity | |||
| 11-dimensional supergravity |
(Here the hat in the lowest row indicates an extended super Minkowski spacetime, which involves higher Cartan geometry.)
To that end, consider the structure of any super Lie algebra
that extends the Poincaré Lie algebra by some odd-graded vector space . Any such extension involves involves:
-
the even-odd superbracket , which hence is an action of the Lorentz Lie algebra on ;
-
the even-even-odd Jacobi identity, which is the action property of that action;
-
the odd-odd superbracket which is a symmetric bilinear form
-
the even-odd-odd Jacobi identity, which says that this bilinear form is -equivariant.
Such structure exists on real spin representation:
Proposition
Let be Minkowski spacetime of some dimension .
The following table lists the irreducible real spin representations of .
| minimal real spin representation | in terms of | supergravity | |||
|---|---|---|---|---|---|
| 1 | real | 1 | |||
| 2 | real | 1 | |||
| 3 | real | 2 | |||
| 4 | 4 | ||||
| 5 | 8 | ||||
| 6 | 8 | ||||
| 7 | 16 | ||||
| 8 | 16 | ||||
| 9 | real | 16 | |||
| 10 | real | 16 | type II supergravity | ||
| 11 | real | 32 | 11-dimensional supergravity |
Here is the 2-dimensional complex vector space on which the quaternions naturally act.
(e.g. Freed 99, page 48)
Remark
The last column in prop. implies that in each dimension there exists a linear map
which is
-
symmetric;
-
-equivariant.
This is what in the physics literature is expressed in components by the Gamma matrices with “indices lowered” using the charge conjugation matrix.
Corollary
Given a real representation , there exists a super Lie algebra structure on
extending the Poincare Lie algebra whose odd-odd-bracket is the bilinear pairing of remark .
Definition
This is the super Poincaré Lie algebra . Its Lie integration to a super Lie group is the super Poincaré group .
The quotient of the super Poincaré Lie algebra by the Lorentz Lie algebra is super-Minkowski spacetime regarded as a super Lie algebra:
Remark
The space underlying the super Minkowski spacetime in def. is the super Cartesian space , def. .
Poincaré connections: Graviton and gravitino field
We may now apply the general discussion of super Lie algebra valued super differential forms, def. , to the case of the super Poincare Lie algebra, def. .
its Chevalley-Eilenberg algebra is generated on
-
elements and of degree
-
and elements of degree
with the differential defined by
Accordingly its Weil algebra has these generators together with a further degree-shifted copy of each , and with differential given by
Differential form data with values in this is a morphism of dg-algebras from the Weil algebra to the deRham dg-algebra , def.
This is ∞-Lie algebroid valued differential form data with ∞-Lie algebroid valued curvature that is explicitly given by:
-
connection forms / field configuration
-
curvature forms / field strengths
-
- the torsion
-
- the Riemann curvature
-
– the covariant derivative of the gravitino
-
Cohomology of super-Minkowski spacetime
The Chevalley-Eilenberg algebras which in def. and def. we used to characterize the corresponding (super) Lie algebras are of course traditionally introduced as the cochain complexes whose cochain cohomology is Lie algebra cohomology. We may conceptualize this as follows:
Definition
For write for the line Lie (n+1)-algebra, the super L-infinity algebra defined simply as the formal dual to the -graded commutative dg-algebra
whose underlying graded algebra is freely generated from a single generator in degree , and whose differential vanishes.
Remark
Recall that being a “formal dual” to a dg-algebra here simply means that for any super Lie algebra, the homomorphisms of super L-infinity algebras of the form
are equivalently (by definition!) homomorphisms of dg-algebras of the form
Since the underlying graded algebra of is free on a single generator in degree , such a homomorphism is determined by the image of this generator
Moreover, the condition that this map respects the differentials, and since the differential on vanishes by definition, this means that
Hence such a moprhism is equivalently a closed element of degree in , hence is equivalently a super Lie algebra cocycle of degree on .
This way line Lie (n+1)-algebra is the moduli object for degree- Lie algebra cohomology in direct analogy of how for instance the familiar Eilenberg-MacLane space is the classifying space for degree ordinary cohomology of topological spaces.
One advantange of conceptualizing Lie algebra cocycles as in remark is that it neatly connects to the formulation of Lie algebra valued forms according to def. , def. :
Remark
A -valued differential form is simply an even closed differential -form:
Hence a super Lie algebra -cocycle on naturally determines a map
given by forming the composite with the morphism representing the cocycle
sending a Lie algebra valued form to a closed differential form .
But an even closed -form on depending on other field data may be understood as the WZW term in a local Lagrangian for the sigma-model of an -brane propagating on . Therefore it is of key interest to classify these for the case that is a super Minkowski spacetime.
Let be the canonical coordinates on the super Minkowski spacetime underlying the super translation group. Then the left invariant super-differential 1-forms are
-
.
-
.
This means that there is one non-trivial differential on these:
These relation consistute .
Remark
The term is sometimes called the supertorsion of the super-vielbein , because the defining equation
may be read as saying that is torsion-free except for that term. Notice that this term is the only one that appears when the differential is applied to “Lorentz scalars”, hence to object in which have “all indices contracted”. (See also at torsion constraints in supergravity.)
Notably we have
This relation is what govers all of the exceptional super Lie algebra cocycles that appear as WZW terms for super p-branes: for some combinations of a Fierz identity implies that the term
vanishes identically, and hence in these dimensions the term
is a cocycle.
Proposition
Lorentz-invariant super Lie algebra cocycles on a super Minkowski spacetime super translation Lie algebra in degree appear precisely once (up to scalar multiple) for each combination for which in string theory there is a super p-brane propagating on a -dimensional supergravity background with -supersymmetries.
The brane scan.
The Green-Schwarz type super -brane sigma-models (see at table of branes for further links and see at The brane bouquet for the full classification):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | M2 | M5 | ||||||||
| 10 | D0 | F1, D1 | D2 | D3 | D4 | NS5, D5 | D6 | D7 | D8 | D9 |
| 9 | * | |||||||||
| 8 | * | |||||||||
| 7 | M2 | |||||||||
| 6 | F1, S1 | S3 | ||||||||
| 5 | * | |||||||||
| 4 | * | * | ||||||||
| 3 | * |
(The first columns follow the exceptional spinors table.)
The corresponding exceptional super L-∞ algebra cocycles (schematically, without prefactors):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | on sIso(10,1) | on m2brane | ||||||||
| 10 | on sIso(9,1) | on StringIIA | on StringIIB | on StringIIA | on sIso(9,1) | on StringIIA | on StringIIB | in StringIIA | on StringIIB | |
| 9 | on sIso(8,1) | |||||||||
| 8 | on sIso(7,1) | |||||||||
| 7 | on sIso(6,1) | |||||||||
| 6 | on sIso(5,1) | on sIso(5,1) | ||||||||
| 5 | on sIso(4,1) | |||||||||
| 4 | on sIso(3,1) | on sIso(3,1) | ||||||||
| 3 | on sIso(2,1) |
The Brane molecule
Furthermore, there exists a more general classification of possible supermembranes in spacetime with spatial dimensions and time dimensions, appearing in (Blencowe-Duff 88). In this sense, the brane scan is but the branch of the brane molecule. The objects appearing here are expected to be related to other generalizations of string theory. See D=12 supergravity and bosonic M-theory.
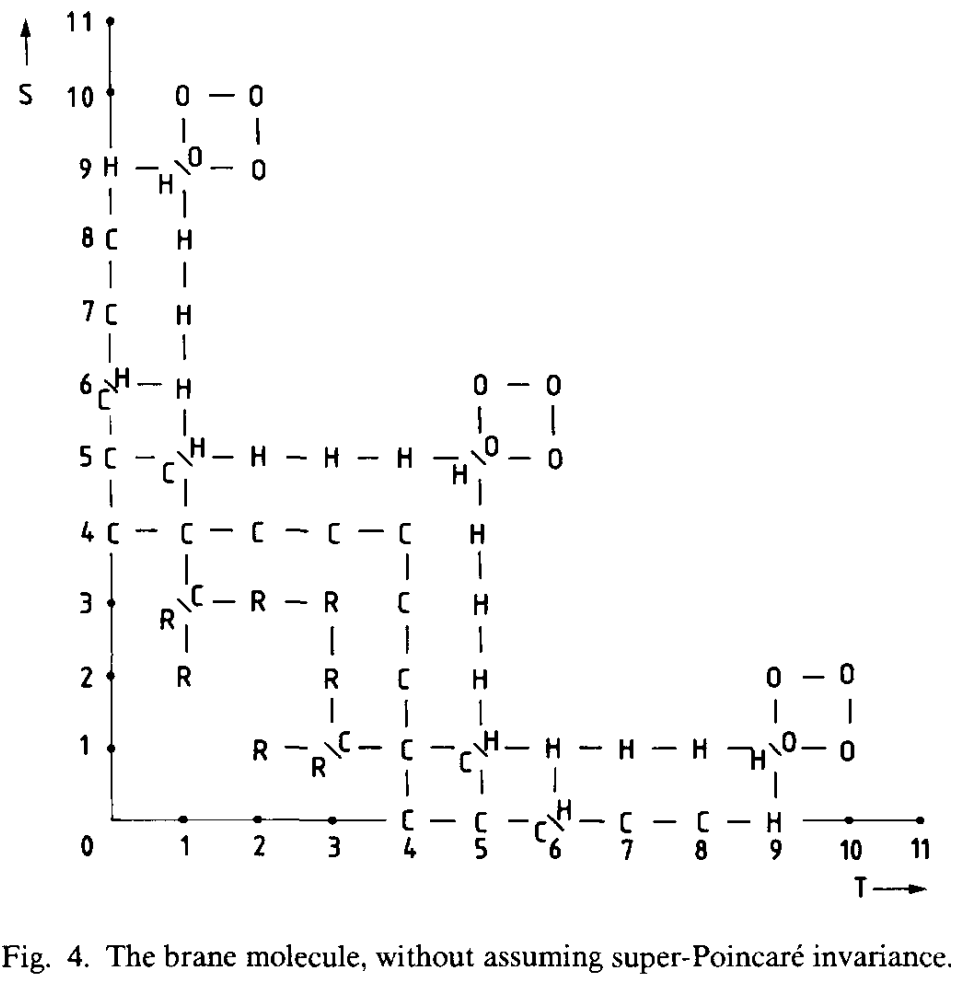
Compare:
-
Miles Blencowe, Mike Duff, Supermembranes and the Signature of Space-time, Nucl. Phys. B310 (1988) 387-404 (spire:262142, 10.1016/0550-3213(88)90155-1, pdf)
Definite super-forms
A rich source of traditional Cartan geometry comes from special holonomy induced by definite forms. We discuss here the analogous phenomenon for super-differential forms which are definite on one of the exceptional closed forms appearing in the brane scan as discussed above.
First consider the traditional situation
Definition
Consider a real vector space and a form regarded as a constant differential form on the smooth manifold underlying .
Consider then a -manifold , i.e. a smooth manifold of dimension . A differential form is a definite form on if its restriction to each tangent space is in the orbit of under the natural action of the general linear group by pullback of differential forms.
Proposition
A choice of definite form, def. , on a -manifold , definite on some is equivalent to a choice of G-structure on for the stabilizer group of under .
Example
For and the canonical symplectic form, then is stabilizer group is the symplectic group and a G-structure in this case is almost symplectic structure.
For and the associative 3-form, then its stabilizer group is G₂ and a G-structure in this case is a G₂-structure.
Now the super differential forms on super Minkowski spacetime in the brane scan serve as curvature forms for the Green-Schwarz super p-brane sigma models on super-Minkowki spacetime. The globalization of these sigma models to curved superspacetimes requires, in particular, that these are extended as definite super differential forms over .
Side Remark
This is discussed further at Green-Schwarz action functional – On curved target spacetime. In fact this is just a necessary condition, giving the globalization of the curvature of the WZW term. The full WZW term is a higher Super Gerbes which is a higher prequantization of this cocycle, and hence its definition requires the lift of the definite cocycle form to a parameterized WZW model over superspacetime. Discussion of this classical anomaly-cancellation problem for super p-branes on curved supergravity targets is the content at Higher Cartan Geometry.
Since the cocycles in the brane scan are not just closed forms, but are also super Lie algebra cocycles, it is natural to ask not for the stabilizer subgroup under the action of the whole general linear group , but just under the automorphism group of the super-Lie bracket, i.e. to ask for stabilization both of the cocycle form as well as the bracket.
Proposition
Let be super Minkowski spacetime in dimension and let the corresponding 3-form characterizing the super-1-brane (superstring) in this dimension, according to the brane scan . Then the stabilizer subgroup of both the super Lie bracket and the cocycle is the Spin group :
This was highlighted by John Huerta.
Proof
It is clear that the spin group fixes the cocycle, and by the discussion at spin representation it preserves the bracket. Therefore it remains to be seen that the Spin group already exhausts the stabilizer group of bracket and cocycle. For that observe that the 3-cocycle is
where is the given Minkowski metric, and that the bilinear map
is surjective. This imples that if preserves both the bracket and the cocycle for all and
then it preserves the Minkowski metric for all
This means that for applications to supergravity the inclusion of supergroups for the corresponding super Cartan geometry is not so much a choice made by hand, as rather being analogous to the G₂-structure which is automatically imposed once one demands a differential form definite on the associative 3-form.
Related entries
References
For references on supergeometry and supermanifolds as such, see there. For references on supergravity as such, see there.
Traditional literature that involves super-Cartan geometry more or less explicitly and in the context of supergravity and its supergravity torsion constraints includes
-
N. S. Baaklini, Spin 3/2 field and Cartan’s geometry, Lett. Math. Phys. 2 (1977) 43-47 [doi:10.1007/BF00420670]
-
N. S. Baaklini, Cartan’s geometrical structure of supergravity, Lett. Math. Phys. 2 (1977) 115-117 [doi:10.1007/BF00398576]
-
Peter van Nieuwenhuizen, Supergravity, Physics Reports, 68, (1981) 189-398 [doi:10.1016/0370-1573(81)90157-5]
-
Riccardo D'Auria, Pietro Fré Geometric Supergravity in D=11 and its hidden supergroup, Nuclear Physics B201 (1982) 101-140
-
Leonardo Castellani, Riccardo D'Auria, Pietro Fré, Supergravity and Superstrings - A Geometric Perspective, World Scientific (1991)
-
John Lott, Torsion constraints in supergeometry, Comm. Math. Phys. 133 (1990) 563-615 [doi:10.1007/BF02097010]
The Geometry of Supergravity Torsion Constraints [arXiv:0108125]
-
José Figueroa-O'Farrill, The homogeneity conjecture for supergravity backgrounds, J.Phys.Conf.Ser.175:012002, 2009 (arXiv:0812.1258)
-
Michel Egeileh, Fida El Chami, Some remarks on the geometry of superspace supergravity, J.Geom.Phys. 62 (2012) 53-60 (spire)
The above material was prepared as lecture notes for
-
Urs Schreiber, Higher Cartan Geometry, lectures at Charles University, Prague (2015)
-
Urs Schreiber, Super Cartan Geometry, lectures at Czech Academy of Science, Prague (2016)
following
remarked upon also in
-
John Huerta, Urs Schreiber, p. 7-8 in: M-theory from the Superpoint, Lett. Math. Phys. 108 (2018) 2695–2727 [doi:10.1007/s11005-018-1110-z, arXiv:1702.01774]
-
John Huerta, Hisham Sati, Urs Schreiber, p. 6-7 in: Real ADE-equivariant (co)homotopy and Super M-branes 371 (2019) 425–524 [doi:10.1007/s00220-019-03442-3, arXiv:1805.05987]
with related lecture notes at:
-
Urs Schreiber, Introduction to Higher Supergeometry, lecture at Higher Structures in M-Theory 2018, Durham Symposium (2018)
partially published as:
Branislav Jurčo, Christian Saemann, Urs Schreiber, Martin Wolf: Higher Structures in M-Theory, Fortschritte der Physik 67 8-9 (2019) [ arXiv:1903.02807, doi:10.1002/prop.201910001]
Super Cartan geometry in more traditional form is made explicit in:
-
Thomas-Paul Hack, Florian Hanisch, Alexander Schenkel: Section 3 of: Supergeometry in locally covariant quantum field theory, Commun. Math. Phys. 342 615 (2016) [doi:10.1007/s00220-015-2516-4, arXiv:1501.01520]
-
Konstantin Eder, Super Cartan geometry and the super Ashtekar connection, Ann. Henri Poincaré 24 (2023) 3531–3599 [arXiv:2010.09630, doi:10.1007/s00023-023-01290-5]
-
Konstantin Eder, Super fiber bundles, connection forms and parallel transport, J. Math. Phys. 62 063506 (2021) [arXiv:2101.00924, doi:10.1063/5.0044343]
briefly reviewed also in:
- James Ratcliffe, §3 in: Supergeometry, Supergravity and Kaluza-Klein Theory, MSc thesis, Imperial College (2022) [pdf, pdf]
Further discussion in relation to the D'Auria-Fre formulation of supergravity:
-
Konstantin Eder, John Huerta, Simone Noja, Poincaré Duality for Supermanifolds, Higher Cartan Structures and Geometric Supergravity [arXiv:2312.05224]
-
Jordan François, Lucrezia Ravera, Cartan geometry, supergravity, and group manifold approach [arXiv:2402.11376]
Last revised on February 13, 2025 at 18:42:07. See the history of this page for a list of all contributions to it.