Schreiber New Foundations for TDA -- Cohomotopy

a brief presentation:

---

• Urs Schreiber on joint work with Hisham Sati:

  
  

  New Foundations for Topological Data Analysis

  The Power of Cohomotopy

  
  

  CQTS$\;$colloquium

  May 2022

about new methods of cohomotopy and specifically of persistent cohomotopy towards more efficient topological data analysis.

• download slides: pdf (to be viewed full screen)

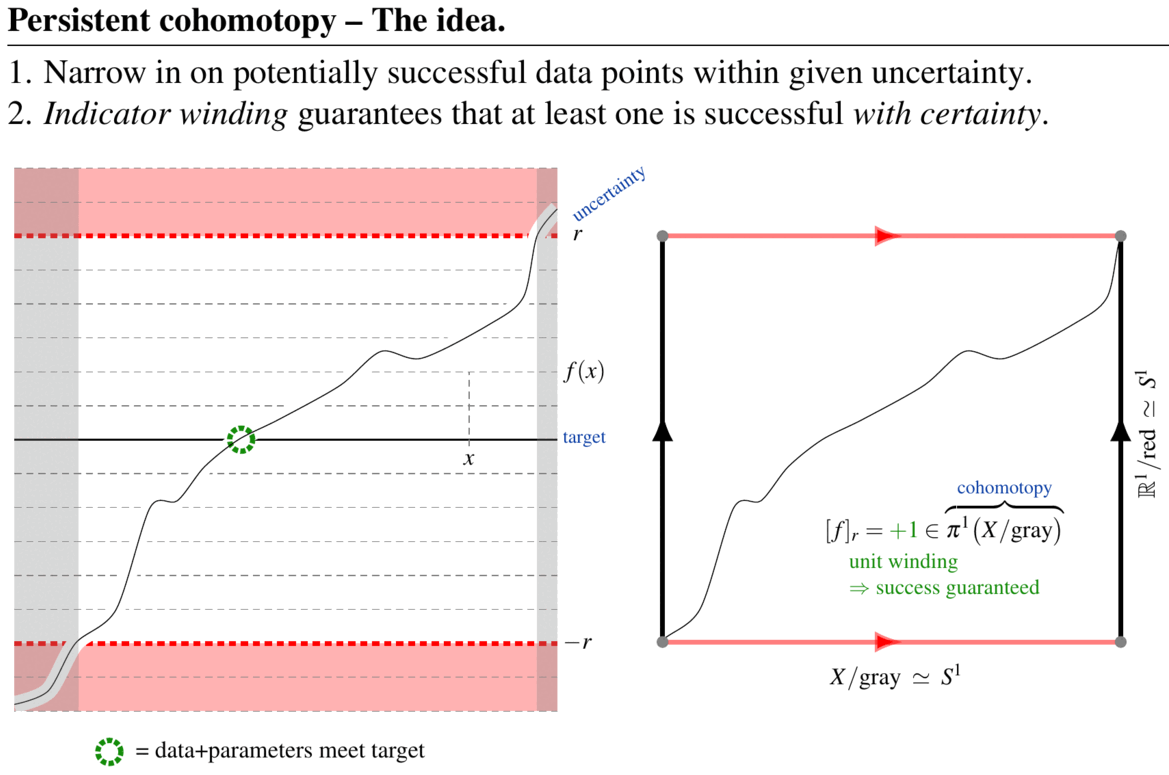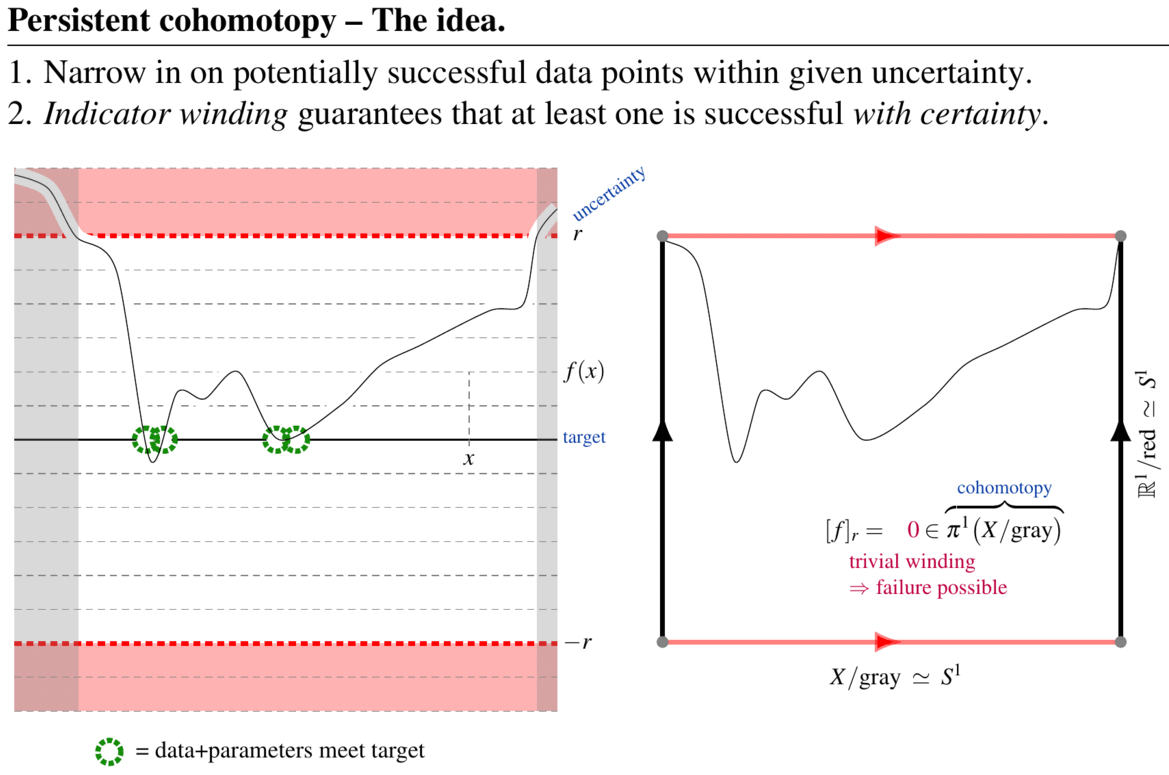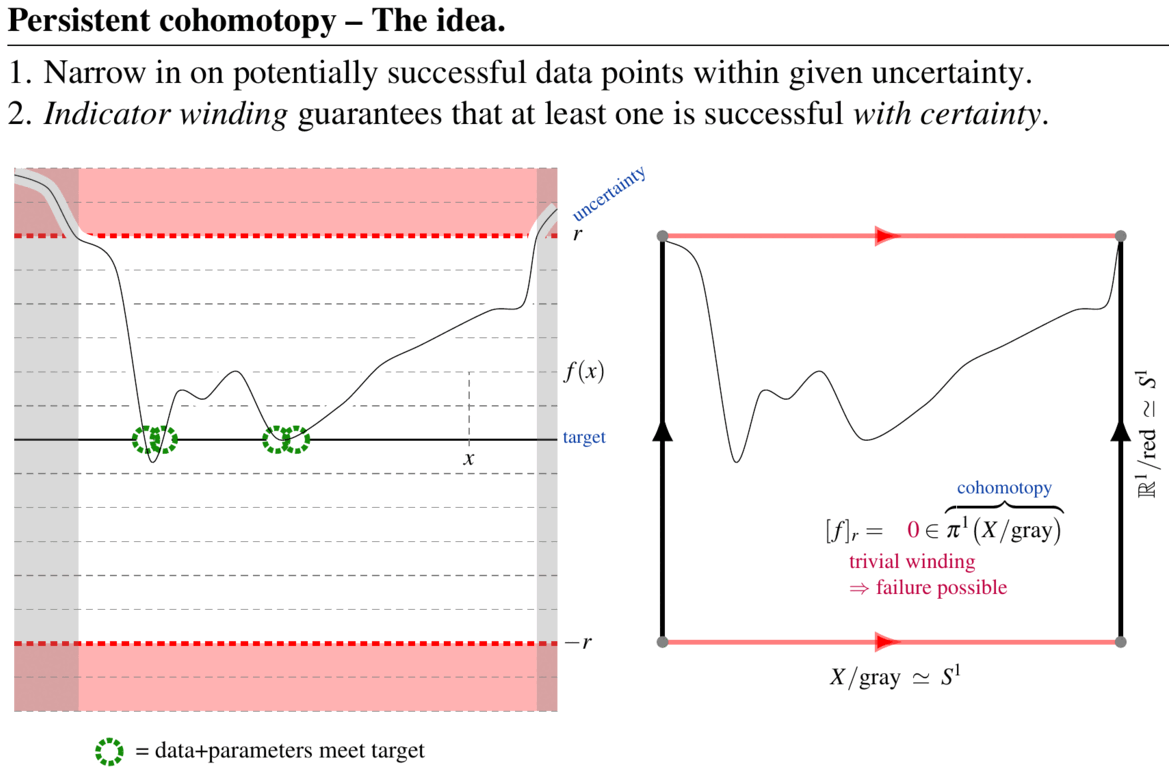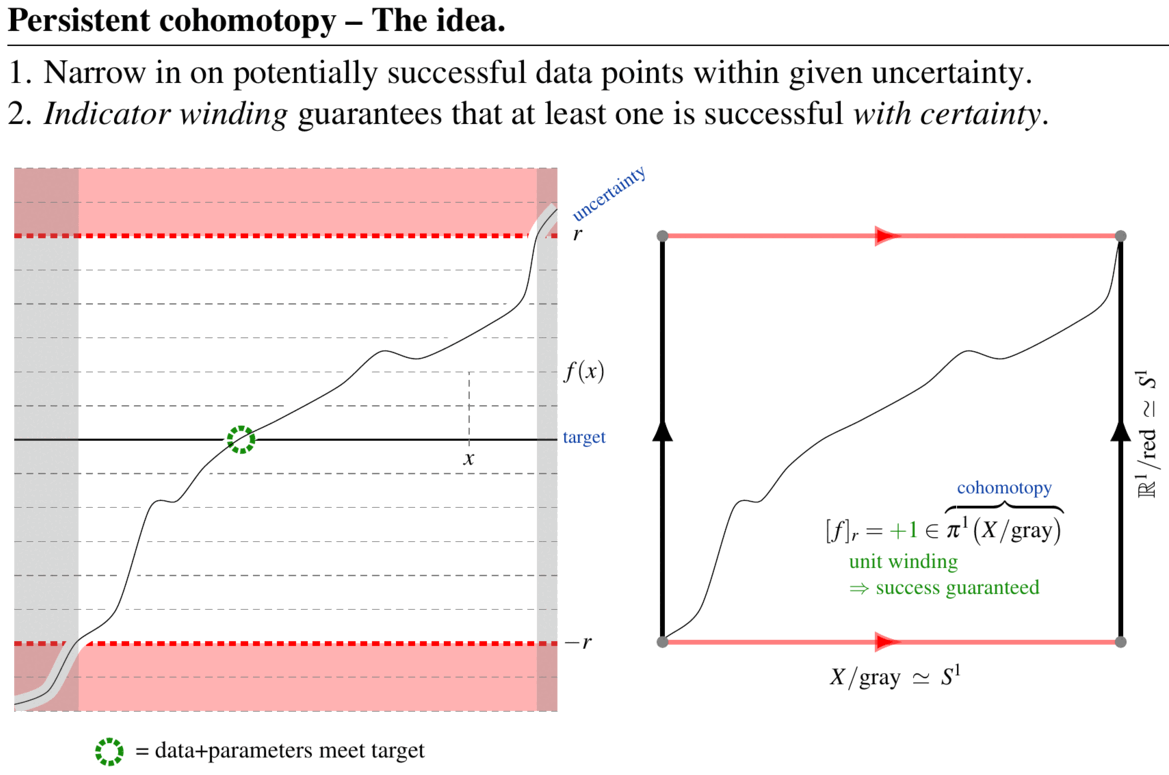
Abstract. The aim of topological data analysis (TDA) is to provide qualitative analysis of large data/parameter sets in a way which is robust against uncertainties and noise. This is accomplished using tools and theorems from the mathematical field of algebraic topology. While a tool called persistent homology has become the signature method of TDA, it tends to produce answers that are either hard to interpret (persistent cycles) or impossible to compute (well groups). Both problems are solved by a variant method $[$FK17$]$ which we may call persistent cohomotopy: A first result shows $[$FKW18$]$ that this new method provides computable answers to the concrete question of detecting whether there exist data+parameters that meet a prescribed target indicator precisely, even in the presence of uncertainty and noise. More generally, efficient data analysis will require further refining persistent cohomotopy to equivariant cohomotopy and/or twisted cohomotopy $[$SS20$]$. Curiously, these flavors of cohomotopy theory have profound relations to formal high energy physics and quantum materials, connecting to which might help to further enhance the power of topological data analysis.

---