nLab persistent cohomotopy

Idea

General

Persistent cohomotopy (not yet an established term) would be the study of cohomotopy in situations where the domain space and/or its map to an n-sphere may depend on a parameter, to yield not just a single cohomotopy set, but a filtered set (a filtered group when the dimension of the domain space is large enough). One concrete implementation of this general notion is considered in Franek & Krčál 2017, see below.

Generally, one may understand persistent cohomotopy both as the dual of persistent homotopy as well as a non-abelian cohomology-version of the more widely considered notion of persistent homology:

	coarse	intermediate	fine
homology	ordinary homology	generalized homology	homotopy
cohomology	ordinary cohomology	generalized cohomology	cohomotopy
persistent homology	persistent ordinary homology	persistent generalized homology	persistent homotopy
persistent cohomology	persistent ordinary cohomology	persistent generalized cohomology	persistent cohomotopy

Detecting data meeting targets

While persistent homology, as a tool in topological data analysis, is traditionally meant to discover persistent cycles in a given data set, it is typically unclear what a persistent cycle actually means for the practical interpretation of the data – certainly this information is not provided by the mathematics.

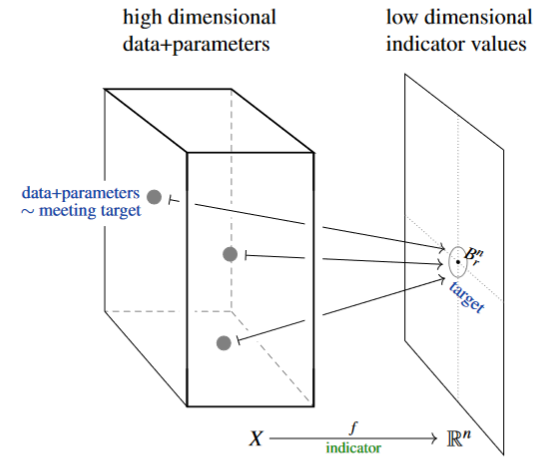
In contrast, persistent cohomotopy in TDA is the effective answer to a concrete and common question in data analysis:

Given a large-dimensional space of data, and a small number $n$ of (real) indicator values assigned to each data point with given precision $1/r$, does any data meet a prescribed target indication precisely?

A fundamental theorem of persistent Cohomotopy (Franek, Krčál & Wagner 2018, Franek & Krčál 2017, p. 5, see Thm. below) shows that (1.) the answer to this question is detected by a certain Cohomotopy-class and (2.) in a fair range of dimensions, this Cohomotopy class is provably computable, hence the above question is effectively decidable. $\phantom{----}$ (figure from SS22)

Alternatively, with tools from persistent homology theory an answer to this question is given by the method of well groups – but (1.) it is known that well groups are in general too coarse to provide a complete answer and (2.) despite effort it remains unknown if well groups are actually computable in relevant cases, see Franek & Krčál 2016.

In this concrete sense (and generally by the above discussion), persistent cohomotopy may be understood as an enhancement or refinement of (well groups in) persistent homology:

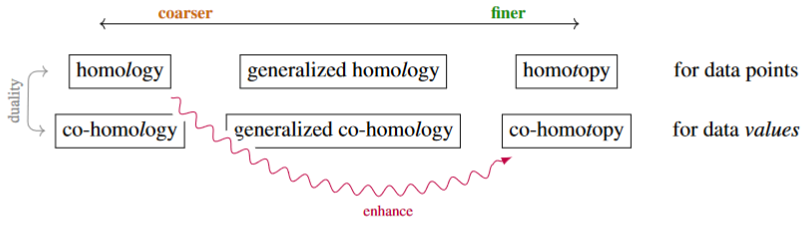
(graphics from SS 22)

Use of cobordism theory

If the topological space $X$ of data may be assumed to be a smooth manifold (indeed, in typical examples $X$ is itself a large-dimensional Cartesian space) then persistent cohomotopy may be understood dually via Pontryagin's theorem as characterizing iso-hypersurfaces of data (close to a given target indicator) by framed cobordism theory (Franek & Krčál 2017, p. 8-9). The full implications of this relation for topological data analysis remain to be explored.

Definition

We spell out the definition considered in Franek & Krčál 2017.

For

• $X$ a topological space,

• $n \in \mathbb{N}$ a natural number,

• $r \in \mathbb{R}_{\gt 0}$ a positive real number,

• $f \,\colon\, X \xrightarrow{\;\;\;\;\;\;} \mathbb{R}^n$ a continuous map,

such that with

• $A_r \,\coloneqq\, f^{-1}\big( \mathbb{R}^n \setminus B_r \big) \;\xhookrightarrow{i_r}\; X\;$

  (the preimage under $f$ of the complement of the open ball of radius $r$ around the origin in the Cartesian space)

we have that

• $(X,A_r)$ is a CW-pair of dimension $dim(X) \leq 2n - 3$,

consider the following induced exact sequence of cohomotopy-groups (where square brackets $[X,Y]$ denote the hom-set $Ho(X,Y)$ in the classical homotopy category, hence homotopy classes of continuous functions $X \to Y$):

Now define what we may call the $n$-cohomotopy of $X$ at resolution $1/r$ relative to $f$, to be (this is FK17 (2)):

(1)$$\pi^n_{(f,r)} \;\coloneqq\; image(\delta_r) \;\simeq\; \Big\{ [g/A_r] \,\in\, \pi^n(X/A_r) \,\big\vert\, (X, A_r) \xrightarrow{ \exists \, g } (\mathbb{R}^n,\, \mathbb{R}^n \setminus B_r) \Big\} \,,$$

hence that subgroup of the $n$-cohomotopy group of the quotient topological space $X/A_r$ whose elements may be represented by continuous maps defined on all of $X$.

Notice that the function $f$ itself canonically represents an element

(2)$$[f]_r \;\in\; \pi^n_{(f,r)}(X)$$

which provides a base point, making this a pointed group.

Moreover, for $r_1 \leq r_2$ we have the evident inclusion

$$A_{r_2} \xhookrightarrow{\; i_{r_1, r_2} \;} A_{r_1}$$

and thus a canonical comparison homomorphisms of pointed groups:

Therefore, regarding the positive real numbers ordered by $\leq$ as a poset and thus as a category, the resulting directed diagram of pointed groups

(3)$$\pi^n_{(f,\bullet)} (X) \;\colon\; (\mathbb{R}, \leq) \xrightarrow{\;\;\;} Grp^{\mathbb{Z}/}$$

is the cohomotopy persistence module (FK17, p. 5, rhyming on persistence module as used in persistent homology theory) of $X$ relative to $f$.

Properties

For $r \in \mathbb{R}_{\gt 0}$, say that a continuous function

$$g\;\colon\; X \xrightarrow{\;\;} \mathbb{R}^n$$

is an $r$-deformation of the given $f$ if its values are pointwise within a radius $r$ of those of $f$, i.e. if

(4)$$\vert g-f\vert_\infty \;\coloneqq\; \underset{x \in X}{max} \vert g(x) - f(x)\vert \;\lt\; r \,.$$

Theorem

(Franek & Krčál 2017, following 2016, p. 5)
Under the above assumptions, the following are equivalent:

• there exists an $r$-deformation (4) of $f$ with no zeros on $X \setminus A_r$;

• the Cohomotopy class $[f]_r \in \pi_n^{(f,r)}(X)$ (2) is trivial.

Moreover, both questions are effectively computable/decidable in the given dimension range.

The proof of the computability statement in Thm. uses a general result about computability of cohomotopy-sets from CKMSVW14.

Examples

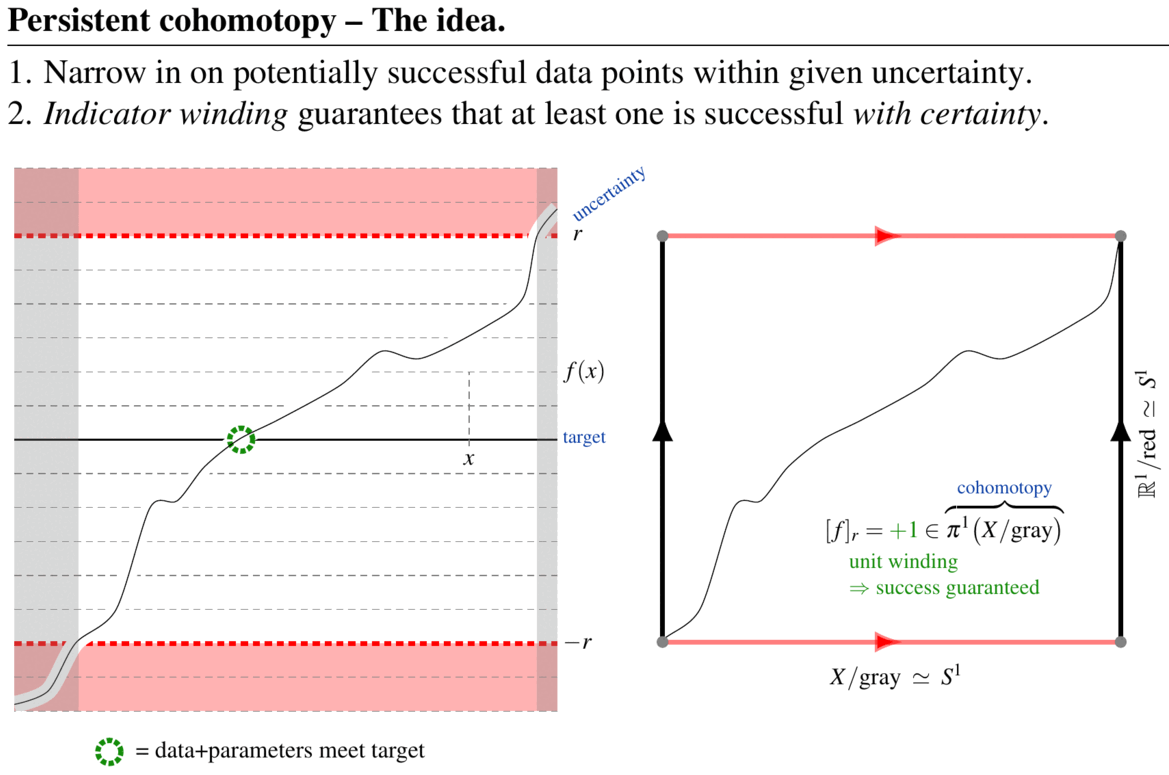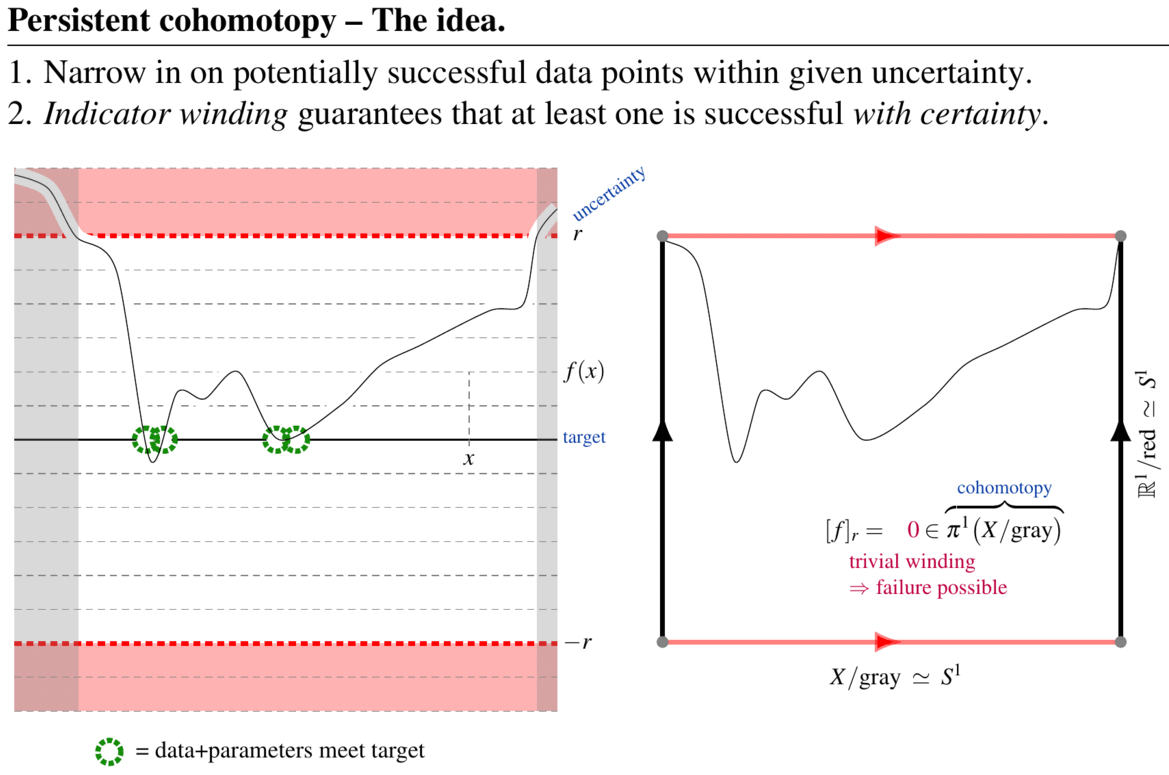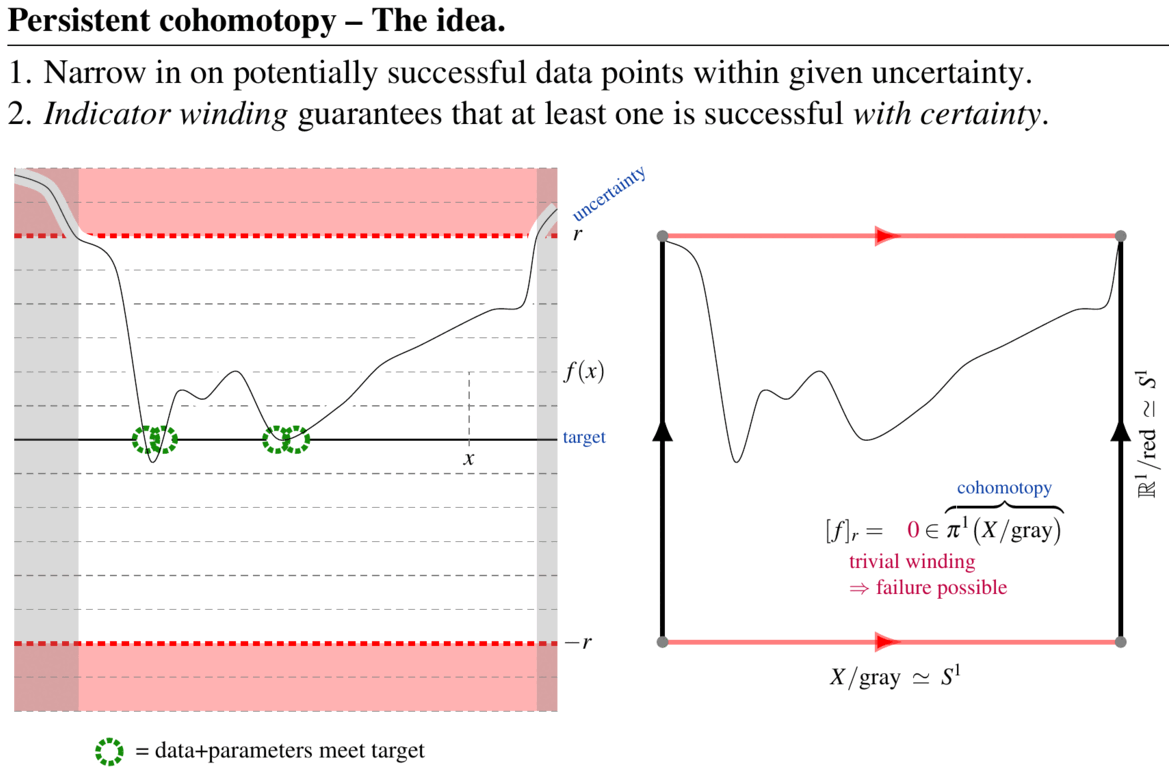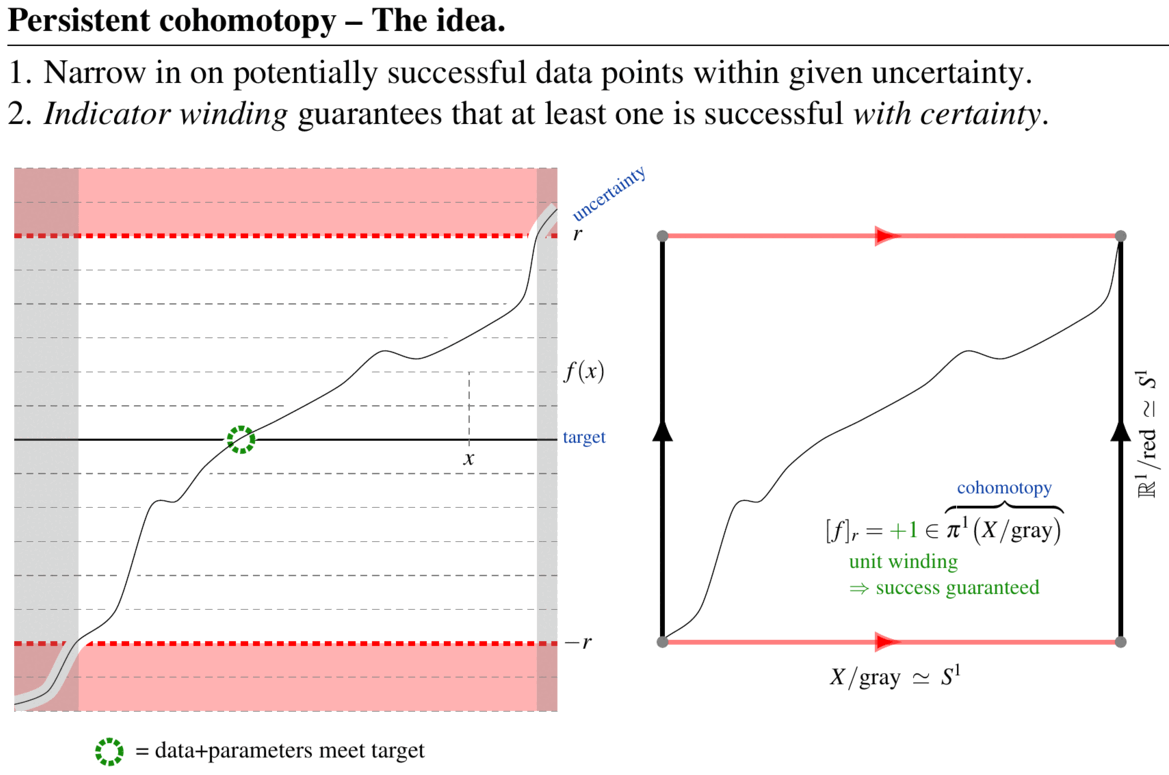
Consider the simplest instructive example, where $X \subset \mathbb{R}$ is an interval (closed or open, such as the real line itself) and $n = 1$.

Notice that $X$ is contractible, so that its plain cohomotopy in positive degree is necessarily trivial, $\pi^{n \geq 1}(X) = \ast$.

Now consider a continuous function

$$f \;\colon\; X \xrightarrow{\;\;} \mathbb{R}^1$$

to the real numbers, and consider the question whether any continuous map that might differ from $f$ by up to $\pm r$ ever takes the value $0 \in \mathbb{R}$.

In this simple case one can decide this immediately by appeal to the intermediate value theorem: Any such function $r$-close to $f$ will have to pass through zero at least once if the values of $f$ ever pass between $(-\infty, -r)$ and $(r, \infty)$. But precisely this is also detected by the 1-cohomotopy class of $f$ at resolution $1/r$ (relative to itself) in the sense of (1), as illustrated in the following figure:

(graphics adapted from SS 22)

Here the curve indicates the graph of $f$ and “gray” stands for the region $A_r \,\subset\, X$, while “red” stands for $\mathbb{R}^1 \setminus B_r$.

One sees on the left that if the cohomotopy class of $f$ at resolution $1/r$ is non-trivial, then there is at least one zero.

In the situation on the right it is intuitively clear that a deformation of $f$ with magnitude smaller than $r$ may move the curve/graph away from the horizontal 0-line. In terms of homotopy theory this is the statement that in this case the quotient-map $X/gray \to \mathbb{R}^1/red$ of $f$ admits a homotopy to the constant function, which shows that its homotopy class (here: a cohomotopy-class) is trivial:

(graphics from SS22)

References

• Peter Franek, Marek Krčál, On Computability and Triviality of Well Groups, Discrete Comput Geom 56 (2016) 126 (arXiv:1501.03641, doi:10.1007/s00454-016-9794-2)

• Peter Franek, Marek Krčál, Persistence of Zero Sets, Homology, Homotopy and Applications, 19 2 (2017) (arXiv:1507.04310, doi:10.4310/HHA.2017.v19.n2.a16)

• Peter Franek, Marek Krčál, Hubert Wagner, Solving equations and optimization problems with uncertainty, J Appl. and Comput. Topology 1 (2018) 297 (arxiv:1607.06344, doi:10.1007/s41468-017-0009-6)

Review:

• Peter Franek, Marek Krčál, Cohomotopy groups capture robust Properties of Zero Sets via Homotopy Theory, talk at ACAT meeting 2015 (pdf slides)

• Urs Schreiber on joint work with Hisham Sati: New Foundations for TDA – Cohomotopy, (May 2022)