nLab Center for Quantum and Topological Systems

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Discuss this page |
Contents
animated logo of CQTS

The Center for Quantum and Topological Systems (CQTS, launched in 2021) is a research center within the Research Institute of New York University in Abu Dhabi.

CQTS is concerned with fundamental questions of quantum systems relevant for quantum technologies — quantum materials, quantum information, quantum sensing, quantum computing, quantum algorithms — with a hallmark focus on foundations of the oft neglected but long-term necessary aspect of topological stabilization via hardware based on topologically ordered phases of quantum materials.

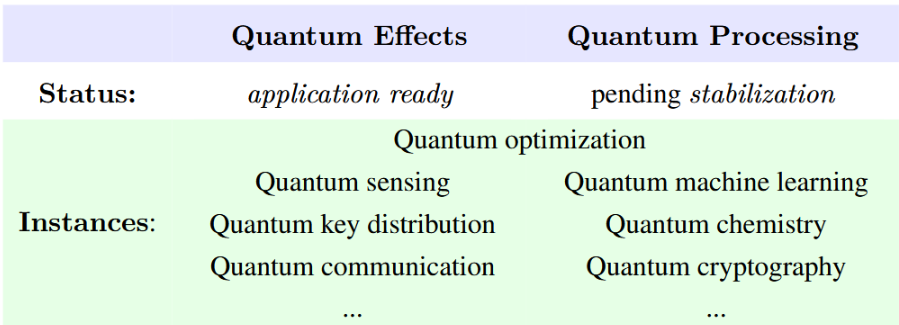
the two kinds of quantum technologies

To this end, the theory heart of the center develops understanding of otherwise elusive strongly cloupled/correlated condensed matter (such as fractional quantum Hall systems) via “geometric engineering on branes” [SS25a], alongside a compatible development of topology-aware quantum programming languages [SS25b, SS25c] based on insights from stable homotopy theory – an approach informed by high energy physics and algebraic topology. At the same time, the center’s Quantum Labs develop spin-based cold atom platforms for quantum sensing [Eq22] and related quantum technologies (such as quantum key distribution) that do not require further stabilization and hence are near-term application ready.


The following lists the center’s public activities, notably local events and local weekly seminars, international and regional events, with further materials (slides, references, videos) provided where available.


Contents


Conferences & Workshops



Jun 2022

Homotopical perspectives on Topological data analysis

Organizers: Sadok Kallel and Hisham Sati



Schedule for 02 June 2022:


  • 15:00 - 16:00 GST/UTC+4

    Ling Zhou (The Ohio State University, USA)

    Persistent homotopy groups of metric spaces

    By capturing both geometric and topological features of datasets, persistent homology has shown its promise in applications. Motivated by the fact that homotopy in general contains more information than homology, we study notions of persistent homotopy groups of compact metric spaces, together with their stability properties in the Gromov-Hausdorff sense. Under fairly mild assumptions on the spaces, we proved that the classical fundamental group has an underlying tree-like structure (i.e. a dendrogram) and an associated ultrametric. We then exhibit pairs of filtrations that are confounded by persistent homology but are distinguished by their persistent homotopy groups. We finally describe the notion of persistent rational homotopy groups, which is easier to handle but still contains extra information compared to persistent homology.


  • 16:00 - 17:00 GST/UTC+4

    Wojciech Chacholski (KTH, Sweden)

    Realisations of Posets

    My presentation is based on an article with the same title coauthored with A. Jin and F. Tombari (arXiv:2112.12209).

    Encoding information in form of functors indexed by the poset of rr-tuples of real numbers (persistence modules) is attractive for three reasons:

    a) metric properties of the poset are essential to study distances on persistence modules

    b) the poset of rr-tuples of real numbers has well behaved discrete approximations which are used to provide finite approximations of persistence modules

    c) the mentioned discretizations and approximations have well studied algebraic and homological properties as they can be identified with multi graded modules over polynomial rings.

    In my talk I will describe a construction called realisation, that transforms arbitrary posets into posets which satisfy all three requirements above and hence are particularly suitable for persistence methods.Intuitively the realisation associates a continuous structure to a locally discrete poset by filling in empty spaces. For example the realisation of the poset of natural numbers is the poset of non-negative reals. I will focus on illustrating how homological techniques, such as Koszul complexes, can be used to study persistence modules indexed by realisations.


  • 17:30 - 18:30 GST/UTC+4

    Grégory Ginot (Université Paris 13, France)

    Homotopical and sheaf theoretic point of view on multi-parameter persistence.

    In this talk we will highlight the study of level set persistence through the prism of sheaf theory and a special type of 2-parameter persistence: Mayer-Vietoris systems and a pseudo-symetry between those. This is based on joint work with Berkouk and Oudot.


  • 18:30 - 19:30 GST/UTC+4

    Rick Jardine (University of Western Ontario, Canada)

    Thoughts on big data sets

    This talk describes work in progress. The idea is to develop methods for analyzing a very large data sets X⊂ℝ NX \subset \mathbb{R}^{N} in high dimensional spaces. There are well-known pitfalls to avoid, including the inability to computationally analyze TDA constructions for XX on account of its size, the “curse of high dimensionality”, and the failure of excision for standard TDA constructions. We discuss the curse of high dimensionality and define a hypercube metric on ℝ N\mathbb{R}^{N} that may lessen its effects. The excision problem for the Vietoris-Rips construction can be addressed by expanding the TDA discussion to filtered subobjects KK of Vietoris-Rips constructions. Unions of such subobjects satisfy excision in path components (clusters) and homology groups, by classical results. The near-term goal is to construct, for each data point xx, a “computable” filtered subcomplex K x⊂V(X)K_{x} \subset V(X) with x∈K xx \in K_{x}, which would capture spatial local behaviour of the data set XX near xx. A large (but highly parallelizable) algorithm finds a nearest neighbour, or a set of kk-nearest neighbours for a fixed data point x∈Xx \in X. Some variant of this algorithm may lead to a good construction of the local subcomplex K xK_{x}.


Jan 2023


−−−−−\phantom{-----} [logo adapted from JMP 62 (2021) 042301]


Feb 2023

24 Feb 2023

CQTS and TII Workshop 2023

joint workshop with the Quantum Research Center (QRC) at the Technology Innovation Institute (TII) in Abu Dhabi

on quantum materials, quantum computation and quantum programming

Break: 10:40 - 11:10

Lunch: 13:00 – 2:15

  • 14:15 - 14:25

    Hisham Sati:

    Introducing research and researchers @CQTS

  • 14:30 - 14:50

    Amaria Javed:

    Quantum information processing via NLS

  • 15:00 - 15:20

    Marwa Mannaï:

    Tuning topological quantum materials

  • 15:30 - 15:50

    Mitchell Riley:

    Verified quantum programming with linear HoTT

Break: 3:50-4:20 pm


Mar 2023

15-18 Mar 2023

Geometric/Topological Quantum Field Theories and Cobordisms (webpage)

on functorial quantum field theory, knot homology and cobordism theory/cobordism categories/cobordism hypothesis

−−−−−\phantom{-----} [logo adapted from arXiv:2103.01877]

\;\;

Mee Seong Im, Mikhail Khovanov, Vivek Singh, Sergei Gukov, Anna Beliakova, Khaled Qazaqzeh

Domenico Fiorenza, Carlo Collari, Sadok Kallel, Nafaa Chbili, Christian Blanchet, David Jaz Myers

\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; Nitu Kitchloo, Daniel Berwick-Evans, Adrian Clough

Sachin Valera, Alonso Perez-Lona, Urs Schreiber \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; Daniel Grady, Christoph Schweigert

\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; Hisham Sati, Konrad Waldorf, Dmitri Pavlov


  • Mikhail Khovanov (Columbia University):

    Universal construction, foams and link homology

    cf.: arXiv:1808.09662, arXiv:2011.11077

    video 1:YT, 2:YT

    In this series of three talks we will explain the foam approach to link homology. Bigraded link homology theories categorify the Jones polynomial and other Reshetikhin-Turaev link invariants, such as the HOMFLY-PT polynomial. Foams, which are polyhedral 2D complexes embedded in 3-space allow to construct state spaces for planar graphs which are then used to define link homology groups. The most explicit and efficient way to define graph state spaces is via evaluation of the closed foams (Robert-Wagner formula).

    A) This formula will be first explained in the less technical unoriented SL(3)SL(3) case. Resulting graph state spaces are then related to the Four-Color Theorem and Kronheimer-Mrowka homology for 3-orbifolds.

    B) A step in that construction requires building a topological theory (a lax TQFT) from an evaluation of closed objects, such as closed nn-manifolds. We will explain the setup for topological theories, including in two dimensions, recovering the Deligne categories and their generalizations. In one dimension and adding defects, these topological theories are related to noncommutative power series, pseudocharacters, and, over the Boolean semiring, to regular languages and automata.

    C) Robert-Wagner GL(N)GL(N) foam evaluation and its application to constructing link homology theories will be explained as well.







  • Mee Seong Im (United States Naval Academy):

    Correspondence between automata and one-dimensional Boolean topological theories and TQFTs

    cf.: arXiv:2301.00700

    video: YT

    Automata are important objects in theoretical computer science. I will describe how automata emerge from topological theories and TQFTs in dimension one and carrying defects. Conversely, given an automaton, there’s a canonical Boolean TQFT associated with it. In those topological theories, one encounters pairs of a regular language and a circular regular language that describe the theory.






  • Nafaa Chbili (United Arab Emirates University):

    Quasi-alternating links, Examples and obstructions

    cf.: arXiv:2009.08624

    video: YT

    Quasi-alternating links represent an important class of links that has been introduced by Ozsváth and Szabó while studying the Heegaard Floer homology of the branched double-covers of alternating links. This new class of links, which share many homological properties with alternating links, is defined in a recursive way which is not easy to use in order to determine whether a given link is quasi-alternating. In this talk, we shall review the main obstruction criteria for quasi-alternating links. We also discuss how new examples of quasi-alternating links can constructed.


  • Khaled Qazaqzeh (Kuwait University):

    On the Finiteness of Quasi-alternating Links

    cf.: arXiv:2208.02984

    slides: pdf

    video: YT

    The generalization of alternating links to quasi-alternating links raises some natural questions that have affirmative answer in the class of alternating links.

    In this talk, we discuss these questions and then we give an affirmative answer to one question without any assumption. As a consequence, we prove that one of these questions is solved in the affirmative iff Green’s conjecture on the finiteness of quasi-alternating links of a given determinant holds. Also, we prove that another question is solved in the affirmative implies Green’s conjecture on the finiteness of quasi-alternating links of a given determinant holds.











Apr 2023


May 2023

22 - 26 May 2023

Quantum Information and Quantum Matter

on quantum information, quantum matter

nyuad.nyu.edu/en/events/2023/may/quantum-information-quantum-matter.html


  • Luigi Amico, (Technology Innovation Institute, Abu Dhabi):

    Coherence of confined matter in lattice gauge theories at the mesoscopic scales

    Atomtronics is the emerging quantum technology of matter-wave circuits which coherently guide propagating ultra-cold atoms. The field benefits from the remarkable progress in micro optics, allowing to control the coherent matter with enhanced flexibility on the micron spatial scale. This way, both fundamental studies in quantum science and technological applications can be carried out. I will sketch recent progress in matter-wave circuitry and atomtronics-based quantum technology. In particular, I will focus on a specific scheme simulating lattice gauge theories and analyze confined matter at the mesoscopic spatial scale.



  • Herbert Schoeller (RWTH Aachen):

    Supersymmetry protected topological states and realization of periodic Witten models in two dimensional second-order topological insulators

    cf.: arXiv:2212.01307

    For a generic two-dimensional topological insulator with band inversion and spin-orbit coupling, we propose the generation of topological zero-energy bound states via the application of an in-plane Zeeman field breaking rotational invariance. The Zeeman field induces a surface gap and generates the topological states via a second-order mechanism generically at the surface positions where the normal component of the Zeeman field vanishes. Via the application of an additional half-integer Aharonov-Bohm flux through a hole of the system, we show that the topological states are protected by supersymmetry. For smooth surfaces, we derive an effective surface Hamiltonian in the form of a periodic Witten model and propose how the surface bound states of the supersymmetric spectrum can be calculated via a trapping mechanism in effective surface potentials. We study the whole phase diagram of the model together with its stability and discuss the high tunability of the topological states.



  • Markus Müller (RWTH Aachen University and Forschungszentrum Jülich, Germany):

    Fault-Tolerant Topological Quantum Computing: From Concepts to Experiments

    To date, the construction of scalable fault-tolerant quantum computers remains a fundamental scientific and technological challenge, due to the influence of unavoidable noise. In my talk, I will first introduce basic concepts of topological quantum error correction codes, which allow one to protect quantum information during storage and processing. I will discuss recent theory work, perspectives and recent collaborative experimental breakthroughs towards fault-tolerant quantum error correction on various physical quantum computing platforms. This includes the first realisation of repeated high-performance quantum error-correction cycles on a topological surface code with superconducting qubits [1], and the first demonstration of a universal and fault-tolerant logical gate set with trapped ions [2]. Furthermore, I will present new fundamental connections between topological quantum error correction and classical statistical mechanics models, in the context of the correction of qubit loss [3,4] and the determination of fundamental error thresholds for circuit noise [5].

    References

    [1] S. Krinner et al., Realizing repeated quantum error correction in a distance-three surface code, Nature 605, 669 (2022)

    [2] L. Postler et al., Demonstration of fault-tolerant universal quantum gate operations, Nature 605, 675 (2022)

    [3] D. Vodola, et al., Twins Percolation

    [4] R. Stricker et al., Deterministic correction of qubit loss, Nature 585, 207 (2020)

    [5] D. Vodola et al., Fundamental thresholds of realistic quantum error correction circuits from classical spin models, Quantum 6, 618 (2022)


  • (…)


Oct 2023

20 Oct 2023

Workshop on Homotopy Theory and Applications



Jan 2024

M-Theory and Mathematics 2024

on January 15 - 17, 2024

at CQTS @ New York University, Abu Dhabi

Speakers:

Alfonsi\,Giotop. Malek Saemann Minasian Lambert Hull Schreiber He Sati X Han Tan Singh Shahbazi Myers Hohm


Talks:

Talks:






  • 15 Jan 2024

    Eric Sharpe:

    Decomposition of 2D Pure Yang-Mills and the Gross- Taylor String Theory

    slides: pdf

    video: kt

    cf.: arXiv:2307.08729

    In this talk, we will attempt to reconcile two different results on two-dimensional pure Yang-Mills theory. Specifically, we will discuss how the fact that 2d pure Yang-Mills is equivalent to a disjoint union of theories, is related to the Gross-Taylor description of 2d pure Yang-Mills as the target-space field theory of a string theory. The Gross-Taylor picture can be understood by first rewriting the Yang-Mills partition function (in a large N N limit) as a sum of correlation functions in Dijkgraaf-Witten theories for the symmetric group S nS_n, and then interpreting those Dijkgraaf-Witten correlation functions in terms of branched covers, which leads to the string theory description. We first observe that the decomposition of the pure Yang-Mills aligns perfectly with the decomposition of S nS_n Dijkgraaf-Witten theory, and then discuss decomposition and the branched covers interpretation. We encounter two puzzles, and to solve them, propose that the Gross-Taylor string theory has a higher-form symmetry.


  • 16 Jan 2024

    Ruben Minasian:

    Constraining and Un-constraining Supergravities

    slides: pdf

    video: kt

    I will review various aspects and somewhat surprising consequences of cancellation of (different types of) anomalies in supergravity theories in eight and six dimensions. I will also discuss appearance and importance of exotic (singular, non-spin, non-orientable) backgrounds.


  • 16 Jan 2024

    Emanuel Malek:

    Kaluza-Klein Spectrometry for String Theory Compactifications

    slides: pdf

    video: kt

    cf.: arXiv:2212.01135

    I will present a powerful new method that for the first time allows us to compute the Kaluza-Klein spectrum of a large class of string theory compactifications, including those arising in maximal gauged supergravities and beyond. This includes geometries with little to no remaining (super-)symmetries, completely inaccessible by previous methods. I will show how these insights can be used to holographically compute the anomalous dimensions of protected and unprotected operators in strongly-coupled CFTs, as well as to study global properties of their conformal manifolds. I will also show how the method can be used to determine the perturbative stability of non supersymmetric AdS vacua. We will see the importance of higher Kaluza-Klein modes to the physics of string compactifications, e.g. in realising the compactness of moduli spaces, restoring supersymmetry that is lost in a consistent truncation, and in destabilising vacua that appear to stable in lower-dimensional supergravities.


  • 16 Jan 2024

    Fei Han:

    Cubic Forms, Anomaly Cancellation and Modularity

    video: kt

    cf.: arXiv:2005.02344

    Freed and Hopkins developed an algebraic theory of cubic forms, which is an analogy to the theory of quadratic forms in topology. They are motivated by the Witten-Freed-Hopkins anomaly cancellation formula in M-theory, which equals a cubic form arising from an E 8 E_8 bundle over a 12 dimensional spin manifold to the indices of twisted Dirac operators on the manifold. In this talk, we will first review the Witten-Freed-Hopkins anomaly cancellation formula and the algebraic theory of cubic forms, and then show that the cubic forms as well as the anomaly cancellation formula can be naturally derived from modular forms that we construct inspired by the Witten genus and the basic representation of affine 𝔢 8 \mathfrak{e}_8 . Following this approach, we obtain new cubic forms and anomaly cancellation formulas on non-spin manifolds and thus provide a unified way to obtain anomaly cancellation formulas of this type. This is based on our joint work with Prof. Ruizhi Huang, Prof. Kefeng Liu and Prof. Weiping Zhang.




  • 16 Jan 2024

    Christian Saemann:

    Atiyah Algebroids for Higher and Groupoid Gauge Theories

    slides: pdf

    video: kt

    We present an Atiyah algebroid picture for higher and groupoid gauge theories. Common to both is the fact that straightforward definitions of curvatures are only suitable for partially flat cases. Instead, one has to adjust the underlying cocycle relations, leading to new curvatures and gauge transformations. The Atiyah algebroid picture I sketch provides a good idea about the origin of adjustments and why they are required even in the relative conventional case of groupoid gauge theories.


  • 17 Jan 2024

    Chris Hull:

    Self-Dual pp-Form Gauge Fields and the Topology of the Graviton

    slides: pdf

    video: kt

    cf.: arXiv:2307.04748

    Sen’s action for a p p -form gauge field with self-dual field strength coupled to a spacetime metric involves an explicit Minkowski metric and the presence of this raises questions as to whether the action is coordinate independent and whether it can be used on a general spacetime manifold. A natural generalisation of Sen’s action is presented in which the Minkowski metric is replaced by a second metric on spacetime. The theory is covariant and can be formulated on any spacetime. The theory describes a physical sector, consisting of the chiral p p -form gauge field coupled to the dynamical metric gg, plus a shadow sector consisting of a second chiral pp-form and the second metric. The resulting theory is covariant and can be formulated on any spacetime. A spacetime with two metrics has some interesting geometry and some of this is explored here and used in the construction of the interactions. The action has two diffeomorphism-like symmetries, one acting only on the physical sector and one acting only on the shadow sector, with the spacetime diffeomorphism symmetry arising as the diagonal subgroup.



  • 17 Jan 2024 (talk canceled last minute and postponed to 31 Jan)

    Chris Blair:

    Geometry and Dualities of Decoupling Limits in String Theory and M-Theory

    cf.: arXiv:2311.10564

    Our understanding of M-theory is based on a duality web connecting different limits of the theory. I’ll discuss the extension of this duality web to a wide variety of decoupling limits related by duality to the null reduction of M-theory (and hence to the proposal that M-theory can be described by Matrix theory). From a modern perspective, these limits involve non-relativistic geometries, leading to new variants of supergravity in 11- and 10-dimensions. I’ll discuss how to systematically explore these corners of M-theory, following the roadmap of arxiv.org/abs/2311.10564.




Apr 2024


17 April 2024

Workshop: Field Theory and Gravity – Classical and Quantum



19-21 April 2024

Conference: Homotopy Type Theory and Computing – Classical and Quantum

home page: nyuad.nyu.edu/en/events/2024/april/homotopy-type-theory-and-computing.html

live stream: nyu.zoom.us/j/93101580794

The aim of this conference is to discuss Homotopy Type Theory Theory (HoTT) as a substrate for computing and verification in software development, in synthetic homotopy theory, and possibly in application to (topological) quantum computing/simulation.

Some talks will focus on recent progress on the general issue of running HoTT programs, in view of the univalence axiom: such as via “cubical TT” or the more recent “higher observational TT”. Other talks will focus on design patterns for practical (quantum) programming and certification languages, notably via modal types and monadic effects (in modal extensions of HoTT).

In this vein, our local speakers will present a point of contact between modal HoTT and Quantum: the recently developed “Linear HoTT” (LHoTT) that equips classical HoTT with dependent “linear” types which may be thought of as quantum data types. The LHoTT approach to quantum programming interprets a significant fragment of the Proto-Quipper-language, now with identity types enabling full verification.

The conference is to bring this theoretical progress into contact with efforts to use (L)HoTT and related languages like Proto-Quipper for actual (quantum) computing, simulation and verification.

Schedule:

19th20th21st
9:00BuchholtzLeeShulman
10:00MörtbergRileyKovács
11:00LamiauxPaykinRiley
12:00LjungströmFinsterlunch
13:00lunchlunch
14:00WärnGratzer
15:00SchreiberSterling
16:00MyersAltenkirch
17:00RandAngiuli

\,

\;\;\;\;\;\;Paykin \;\;\;\;Wärn \; Myers \;\;\; Kovács \;\;\; Finster \; Schreiber \;\;\;X \;\;\; Altenkirch \; Lamiaux \;Riley \;\;\; Buchholtz \;\;\; Lee

Talks:


May 2024


27 May - 31 May 2024

Conference: Quantum Information and Quantum Matter

home page: nyuad.nyu.edu/en/events/2024/may/quantum-information-and-quantum-matter.html


Talks:

  • Herbert Schoeller (RWTH Aachen University):

    Universal Properties of the Boundary Charge

    The boundary charge is an interesting observable to characterize ground state properties of insulators. Its universal properties and relevance for topology, bulk-boundary correspondence, integer and fractional quantum Hall effect, charge quantization, universal fluctuations, and characterization of phase transitions is reviewed in this talk. In particular, it is demonstrated that two fundamental invariants characterize the properties of the boundary charge, which are present independent of symmetries, and are the basis for the explanation of the quantum Hall effect and the rational quantization of boundary and interface charges.

  • Christina Psaroudaki (École Normale Supérieure (ENS)):

    Quantum Functionalities of Magnetic Skyrmions

    Magnetic nanoskyrmions develop quantized helicity excitations, and the quantum tunneling between nanoskyrmions possessing distinct helicities is indicative of the quantum nature of these particles. Experimental methods capable of non-destructively resolving the quantum aspects of topological spin textures, their local dynamical response, and their functionality now promise practical device architectures for quantum operations. With abilities to measure, engineer, and control matter at the atomic level, nanoskyrmions present opportunities to translate ideas into solid-state technologies. This talk aims to discuss the basic concept of a magnetic skyrmion qubit, its advantages, and challenges in this new research avenue in quantum magnetism and quantum information.

  • Ajit C. Balram (Homi Bhabha National Institute, India):

    Fingerprints of Composite Fermion Lambda Levels in Scanning Tunneling Microscopy

    cf. arXiv:2312.06779

    Composite fermion (CF) is a topological quasiparticle that emerges from a non-perturbative attachment of vortices to electrons in strongly correlated two-dimensional materials. Similar to non-interacting fermions that form Landau levels in a magnetic field, CFs can fill analogous “Lambda’‘ levels, giving rise to the fractional quantum Hall (FQH) effect of electrons. Here, we show that Lambda levels can be directly visualized through the characteristic peak structure in the signal obtained via spectroscopy with the scanning tunneling microscopy (STM) on a FQH state. Complementary to transport, which probes low-energy properties of CFs, we show that high-energy features in STM spectra can be interpreted in terms of Lambda levels. We numerically demonstrate that STM spectra can be accurately modeled using Jain’s CF theory. Our results show that STM provides a powerful tool for revealing the anatomy of FQH states and identifying physics beyond the non-interacting CF paradigm.

  • Yuxin Zhao (University of Hong Kong):

    Projective Crystal Symmetry and Novel Topological Phases

    Roughly a decade after the birth of quantum mechanics, E. Wigner pointed out a fundamental principle of quantum mechanics: symmetry groups are projectively represented. He applied this principle to study the Poincaré group. While the Poincaré group is the unique spacetime group of relativistic particles, its counterpart in condensed matter consists of various space groups for crystals and the time reversal. In this sense, the projective representation of condensed-matter spacetime groups is much richer and of fundamental importance. However, projective crystal symmetry was not systematically investigated until recently. In this talk, I will introduce the general theory of projective crystal symmetry algebras and show some of their novel consequences in topological matter. Particularly, they can lead to kk-space non-symmorphic symmetries, which can significantly expand the framework of crystalline topological phases.

  • Leandro Aolita (Quantum Research Center, TII, Abu Dhabi):

    Tensor Network Use Cases: From Quantum Process Tomography to Computational Fluid Dynamics

    In this talk, I will describe two recent applications of tensor networks. In the first part, I will present an efficient technique for quantum process learning, a quintessential primitive to characterize quantum devices. This combines a tensor network representation of the target quantum channel with a data-driven optimization inspired by unsupervised machine learning. These results go far beyond state-of-the-art, providing a practical and timely tool for benchmarking quantum circuits in current and near-term quantum computers. In the second part, in turn, I will briefly describe a recently developed (classical) quantum-inspired algorithm for solving the Navier-Stokes equation in complex geometries, based on tensor trains. This is a full-stack method to solve for incompressible fluids with memory and runtime scaling poly-logarithmically in the mesh size. Our framework is based on matrix product states (a.k.a tensor trains), a powerful compressed representation of quantum states. It is complete in that it solves for flows around immersed objects of arbitrary geometries, with non-trivial boundary conditions, and self-consistent in that it can retrieve the solution directly from the compressed encoding, i.e. without ever passing through the expensive dense-vector representation. This machinery lays the foundations for a new generation of potentially radically more efficient solvers of real-life fluid problems.

  • Ingo Roth (Quantum Research Center, TII, Abu Dhabi):

    Robustly Learning the Hamiltonian Dynamics of a Superconducting Quantum Processor

    The required precision to perform quantum simulations beyond the capabilities of classical computers imposes major experimental and theoretical challenges. The key to solving these issues are highly precise ways of characterizing analog quantum simulators. Here, we report on theoretical and experimental work on estimating the free Hamiltonian parameters of bosonic excitations in a superconducting-qubit analog quantum simulator from measured time-series. We achieve the required levels of precision in estimating the Hamiltonian parameters by maximally exploiting the model structure, making it robust against noise and state-preparation and measurement (SPAM) errors. Our learning algorithm is highly scalable both in terms of the required amounts of data and post-processing. To achieve this, we develop a new super-resolution technique for frequency extraction from matrix time-series and make use of constrained manifold optimization for the eigenspace reconstruction. For up to 14 coupled superconducting qubits on two Sycamore processors, we identify the Hamiltonian parameters - verifying the implementation on one of them up to sub-MHz precision - and construct a spatial implementation error map for a grid of 27 qubits. Our results constitute a fully characterized, highly accurate implementation of an analog dynamical quantum simulation and introduce a diagnostic toolkit for understanding, calibrating, and improving analog quantum processors.


  • Enrique Solano (Kipu Quantum, Berlin, Germany):

    Useful Quantum Computing in the NISQ Era

    I will describe digital, analog, and digital-analog quantum computing paradigms. Furthermore, I will discuss the possibility of reaching quantum advantage for industry use cases with current quantum computers in trapped ions, superconducting circuits, neutral atoms, and photonic systems.

  • Javad Shabani (NYU New York):

    Experimental Routes in Realization of Topological Josephson Junctions

    Majorana bound states, which are their own antiparticles, are predicted to emerge as zero-energy modes localized at the boundary between a topological superconductor and a topologically trivial region. Unlike BCS superconductors, nature has not provided us unambiguous topological superconductors. However, it was realized that by interfacing BCS superconductors and semiconductors with strong spin-orbit coupling it is possible to create a system that can host topological states. Hence epitaxial superconductors and semiconductors have emerged as an attractive materials system with atomically sharp interfaces and broad flexibility in device fabrications incorporating Josephson junctions. We discuss the basics of topological superconductivity and provide insight on how to go beyond current state-of-the-art experiments. We argue that the ultimate success in realizing Majorana bound state physics relies on the observation of non-trivial fusion and braiding experiments.

  • Frank Schindler (Imperial College London):

    Interaction-Induced Crystalline Topology of Excitons

    Topologicalband theory has celebrated various successes over the last few years, such as the recent classifications of crystalline materials based on their space group symmetry. We are currently witnessing a drive to generalise this theory to the case where interactions between electrons become relevant, with much work focused on ground states. As an alternative direction, we here study the topology of interaction-induced excitations, specifically excitons in semiconductors. In my talk, I will give a pedagogical introduction to the classification and bulk-boundary correspondence of exciton band structures based on inversion symmetry.

  • Adrien Bouhon (Nordic Institute for Theoretical Physics, Sweden):

    From the Homotopy Groups of Real Grassmannians to the Quantum Geometry of Many-Band Systems

    I first review the homotopy classification of band structures for crystalline systems described by a real Bloch Hamiltonian. These systems, both of fermionic or bosonic types, abound in nature as they merely require the combination of an anti-unitary symmetry (e.g. time reversal) and a twofold unitary symmetry (i.e. inversion, Pi-rotation, or mirror). The relevant classifying spaces, i.e. the real Grassmannians and the real flag manifolds, exhibit a rich geometric structure leading to a manifold of topological phases in all dimensions. I then introduce a completely general framework, based on the Pluecker imbedding of Grassmannians, to capture the Riemannian geometry of these “real” topological phases, that naturally extends to many-band contexts. While this approach permits the systematic homotopy-based modeling of few-band systems — greatly facilitating the design of such phases in synthetic matter — it culminates with the definition of a new ℤ\mathbb{Z} invariant capturing the Euler class of many-band (i.e. beyond rank-2) subspaces.

  • András Pályi (Budapest University of Technology and Economics):

    Weyl Points Beyond Band Structures: Classical Mechanics, Spin Qubits, Josephson Junctions

    In the past decade, research on Weyl semimetals has evolved into a major theme within condensed-matter physics. Defining characteristics of Weyl semimetals are Weyl points, i.e., touching points (a.k.a. degeneracy points or conical intersections) between neighbouring energy bands in the electronic band structure. Further characteristics of such a Weyl point are its robustness against fluctuations, and the linear energy dispersion in its vicinity. In this talk, I will discuss the simple mathematical origin of the robustness of Weyl points, and illustrate that similar degeneracy points appear in a plethora of physical systems described by parameter-dependent matrices, e.g., in the frequency spectrum of coupled linear oscillators [1], and in the energy spectrum of interacting spin qubits [2,3,4] or Josephson junctions [5,6]. I will also highlight universal patterns describing the creation, annihiliation, merger, and separation of Weyl points as control parameters are varied [6,7]. Interestingly, much of this universal behaviour is described by known results from a specific branch of mathematics called singularity theory.

    [1] Z. Guba, Gy. Frank, G. Pinter, A. Palyi, Weyl points in ball-and-spring mechanical systems, arXiv:2302.08241

    [2] Z. Scherubl, A. Palyi, et al., Observation of spin-orbit coupling induced Weyl points in a two-electron double quantum dot, Comms. Phys. 2, 108 (2019), arXiv:1804.06447

    [3] Gy. Frank, Z. Scherubl, Sz. Csonka, G. Zarand, A. Palyi, Magnetic degeneracy points in interacting two-spin systems: geometrical patterns, topological charge distributions, and their stability, Phys. Rev. B 101, 245409 (2020), arXiv:1910.02831

    [4] A. Sen, Gy. Frank, B. Kolok, J. Danon, A. Palyi, Classification and magic magnetic-field directions for spin-orbit-coupled double quantum dots, Phys. Rev. B 108, 245406 (2023), arXiv:2307.02958

    [5] Gy. Frank, D. Varjas, G. Pinter, A. Palyi, Weyl-point teleportation, Phys. Rev. B 109, 205415 (2024), arXiv:2112.14556

    [6] Gy. Frank, G. Pinter, A. Palyi, Singularity theory of Weyl-point creation and annihilation, arXiv:2309.05506

    [7] G. Pinter, Gy. Frank, D. Varjas, A. Palyi, Birth Quota of Non-Generic Degeneracy Points, arXiv:2202.05825

  • Rafael Chaves (International Institute of Physics (IIF-UFRN))

    Enhancing Non-Classicality Detection with Interventional Data

    Generalizations of Bell's theorem, particularly within quantum networks, are now being analyzed through the causal inference lens. However, the exploration of interventions, a central concept in causality theory, remains unexplored. As will be discussed, if we are not limited to observational data and can intervene in our experimental setup, then we can witness quantum violations of classical causal bounds even when no Bell-like violation is possible. That is, through interventions, the quantum behavior of a system that would seem classical otherwise can be demonstrated. We will then present a photonic experiment implementing those ideas and consider applications of this framework for measurement-based quantum computation, quantification of causality in quantum gates and quantum network protocols.

    [1] M. Gachechiladze et al. “Quantifying causal influences in the presence of a quantum common cause.” Physical Review Letters 125, 230401 (2020).

    [1] I. Agresti et al. “Experimental test of quantum causal influences.” Science Advances 8, eabm1515 (2022).

    [1] P. Lauand et al. “Quantum non-classicality in the simplest causal network.” arXiv preprint arXiv:2404.12790 (2024).

  • Sonia Haddad (University of Tunis El Manar):

    Altermagnetism Emerging from Electronic Correlations

    While altermagnetic materials are characterized by a vanishing net magnetic moment, their symmetry in principle allows for the existence of an anomalous Hall effect (AHE). Here we introduce a model with altermagnetism in which the emergence of an AHE is driven by interactions. This model is grounded in a modified Kane-Mele framework with antiferromagnetic (AFM) spin-spin correlations. Quantum Monte Carlo simulations show that the system undergoes a finite temperature phase transition governed by a primary AFM order parameter accompanied by a secondary one of Haldane type. The emergence of both orders turns the metallic state of the system, away from half-filling, to an altermagnet with a finite anomalous Hall conductivity. A mean field ansatz corroborates these results, which pave the way into the study of correlation induced altermagnets with finite Berry curvature.

  • Gianluigi Catelani (Quantum Research Center, TII, Abu Dhabi):

    Improved Modelling of Superconducting Qubits

    More accurate control and reduced error rates are needed for superconducting circuits to move beyond the current NISQ era, and improving our understanding of superconducting qubits can help towards this goal. In this talk I will discuss two recent advances and their impacts on qubit control and errors. After briefly reviewing the standard tunnel model of a Josephson junction, I will introduce a more realistic model which is needed to accurately describe spectroscopic data [1]. Next, I will show how a form of so-called “gap engineering’’, in which the values of the superconducting gap on the two sides of a junction are properly chosen, can mitigate errors related to quasiparticles [2]. Finally, I will consider implications for a proposed topological qubit implementation (see [3] and references there).

    [1] D. Willsch et al., Nat Phys (2024)

    [2] G. Marchegiani et al., PRX Quantum 3, 040338 (2022)

    [3] J. Krause et al., arXiv:2403.03351

  • Felix von Oppen (Dahlem Center for Complex Quantum Systems, Freie Universität Berlin):

    Theory of the Quantum Twisting Microscope

    2D van der Waals systems have become a major quantum materials platforn, exhibiting a plethora of correlated electronic phases. Beyond conventional transport experiments, much information on van-der-Waals materials derives from local probes such as scanning tunneling microscopy as well as scanning single-electron-transitor and scanning SQUID measurements. The quantum twisting microscope is a powerful new instrument complementing previously existing local probes. Rather than measuring the local tunneling current at the atomic scale as in scanning tunneling microscopy, it relies on coherent tunneling across a twistable finite-area junction formed at the interface between van der Waals systems placed on a scanning tip with a flat pyramidal top and a substrate. Due to the finite contact area, tunneling is momentum conserving up to reciprocal lattice vectors of the tip and sample layers. In this talk, I discuss the theory of the quantum twisting microscope. While elastic tunneling dominates the tunneling current at small twist angles, the momentum mismatch between the K-points of tip and sample at large twist angles can only be bridged by inelastic scattering. The latter allows for probing collective-mode dispersions along certain lines in reciprocal space by measuring the tunneling current as a function of twist angle and bias voltage. We illustrate this modality of the quantum twisting microscope by developing a systematic theory for measuring phonon dispersions using graphene-graphene junctions. In addition to providing a case study for probing collective modes, our results inform the quest to understand the origin of superconductivity in twisted bilayer graphene.

  • Robert-Jan Slager (University of Cambridge):

    Non-abelian Phases, Geometry and Quantised Responses

    In this talk I will talk about non-Abelian band topology and the connection to Riemannian geometry. I will discuss how these ideas culminate in the prediction of quantized shift photoconductivities and show that this response may be recast in terms of the integrated torsion tensor and the non-Abelian Berry connection constituting Chern-Simons forms. Physically, I will motivate that the topological quantization emerges purely from virtual transitions contributing to the optical response and discuss possible generalisations.

  • Xiong-Jun Liu (International Center for Quantum Materials, Peking University):

    Quantum Critical States in Quasiperiodic Lattices: From Non-Interacting to Correlated

    The disordered quantum systems host three types of fundamental quantum states, the extended, localized, and critical states, of which the multifractal critical states are much less understood compared with the former two. Conventionally the characterization of the quantum critical states relies on arduous numerical verification. In this talk, I will present a systematic analytic and numerical study of the critical states in quasiperiodic systems, with or without particle-particle interactions. Through the Avila global theory, a Fields Medal work which we introduce for the first time to cold atoms, we propose a class of exactly solvable models, dubbed mosaic lattice models, hosting novel types of exact mobility edges separating localized from quantum critical or extended states, With these exactly solvable models, we discover a universal mechanism for the critical states that the such states are due to the vanishing Lyapunov exponent and the incommensurately distributed hopping zeros in the thermodynamic limit, which also serve as a rigorous characterization of the critical states. We further show that in the presence of interactions, the critical states turn into the many-body counterparts upon the finite-size scaling analysis, giving a many-body critical phase, which is an exotic phase in-between the thermal phase and many-body localization. Based on the considerable progresses in spin-orbit coupled optical Raman lattices, which have been widely applied to simulate topological phases, we discuss our latest experimental realization of the present predictions. Future important issues will be commented.

  • Pramod Padmanabhan (Indian Institute of Technology Bhubaneswar):

    Braid and Higher Simplex Operators in Integrable Quantum Computing

    Two-qubit Yang-Baxter or braiding gates casts quantum computing as a scattering process. Due to the many conserved quantities this procedure is less noisy. Generalising this to 3-and higher-qubit gates relies on solutions to the tetrahedron and higher simplex equations. We will construct such gates systematically using Clifford algebras. The resulting gates are potentially more effective in simulating different quantum algorithms.

  • Po-Yao Chang (National Tsing Hua University in Taiwan):

    Entanglement Diagnosis of Many-Body Systems: Applications to Non-Unitary Conformal Field Theory and Topological Quantum Field Theories

    Entanglement measures provide powerful tools for diagnosing quantum many-body phases of matter. In particular, in (1+1)-dimensional systems with conformal symmetry, entanglement entropy exhibits logarithmic scaling, where the coefficient determines the central charge of the underlying conformal field theory (CFT). However, in the absence of the unitary condition, the central charge can be negative, leading to negative entanglement entropy. To address this issue, we propose the generalized entanglement entropy to extract the negative central charges in several examples. In addition, in (2+1)-dimensional systems described by topological quantum field theories (TQFT), the sub-leading term of the entanglement entropy is referred to as the topological entanglement entropy (TEE), which contains information about the topological data of the quasiparticles. In this talk, I would like to discuss the TEE for different bipartitions.

  • Tim Byrnes (NYU Shanghai):

    Unified Framework for Efficiently Computable Quantum Circuits

    Quantum circuits consisting of Clifford and matchgates are two classes of circuits that are known to be efficiently simulatable on a classical computer. We introduce a unified framework that shows in a transparent way the special structure that allows these circuits can be efficiently simulatable. The approach relies on analyzing the operator spread within a network of basis operators during the evolution of quantum circuit. Quantifying the complexity of a calculation by the number of operators with amplitude above a threshold value, we show that there is a generic form of the complexity curve involving an initial exponential growth, saturation, then exponential decay in the presence of decoherence. Our approach is naturally adaptable into a numerical procedure, where errors can be consistently controlled as a function of the complexity of the simulation.

  • Arijeet Pal (University College, London):

    Long Range Entanglement in Measurement Induced Phases

    In this talk, I will describe two recent applications of tensor networks. In the first part, I will present an efficient technique for quantum process learning, a quintessential primitive to characterize quantum devices. This combines a tensor network representation of the target quantum channel with a data-driven optimization inspired by unsupervised machine learning. These results go far beyond state-of-the-art, providing a practical and timely tool for benchmarking quantum circuits in current and near-term quantum computers. In the second part, in turn, I will briefly describe a recently developed (classical) quantum-inspired algorithm for solving the Navier-Stokes equation in complex geometries, based on tensor trains. This is a full-stack method to solve for incompressible fluids with memory and runtime scaling poly-logarithmically in the mesh size. Our framework is based on matrix-product states (a.k.a tensor trains), a powerful compressed representation of quantum states. It is complete in that it solves for flows around immersed objects of arbitrary geometries, with non-trivial boundary conditions, and self-consistent in that it can retrieve the solution directly from the compressed encoding, i.e. without ever passing through the expensive dense-vector representation. This machinery lays the foundations for a new generation of potentially radically more efficient solvers of real-life fluid problems.

  • Alioscia Hamma (University of Naples Federico II):

    Non-stabilizerness in Quantum Mechanics

    We all know that entanglement is important in quantum mechanics. However, quantum behavior needs a second ingredient, the so-called non-stabilizerness property, commonly known as magic. Without it, no quantum computer would be able to outperform a classical one, but not only. Quantum chaos would not ensue, and quantum thermodynamics would not be the same. Bell's inequalities would not be violated, and black holes would always be easy to decode. Quantum many-body systems would be boring. Also all the probabilities that come from the Born rule would be trivial. Finally, without non-stabilizerness there would also be no gravity, according to the AdS/CFT conjecture.
 All these features are captured by the notion of Stabilizer Entropy (SE), which we will introduce and explain in this talk.

  • Markus Müller (RWTH Aachen University, Germany):

    The Dawn of Quantum Fault-Tolerance

    The construction of scalable fault-tolerant quantum computers remains a fundamental scientific and technological challenge, due to the influence of unavoidable noise. In my talk, I will first introduce basic concepts of quantum error correction, which allows one to protect quantum information during storage and processing. I will in my talk present new theory concepts and recent collaborative experimental advances towards fault-tolerant quantum error correction on various physical quantum computing platforms. Specifically, I will present new fault-tolerance preserving protocols for autonomous quantum error correction [1], which do not require in-sequence measurements of qubits, which are often slow or technically challenging in many state-of-the-art physical quantum processor platforms. I will also show how quantum cellular automata can be designed to give rise to emergent many-body dynamics with quantum error-correcting capabilities [2]. Towards universal fault-tolerant quantum computing with logical qubits — eventually outperforming computations executed on their physical qubit counterparts — I will present new protocols [3] and first experimental demonstrations [4] of fault-tolerant code switching.

    [1] S. Heußen et al., Measurement-free fault-tolerant quantum error correction in near-term devices, PRX Quantum 5, 010333 (2024)

    [2] T. L. M. Guedes et al., Quantum cellular automata for quantum error correction and density classification, arXiv:2309.03608 (2023)

    [3] F. Butt et al., Fault-Tolerant Code Switching Protocols for Near-Term Quantum Processors, arXiv:2306.17686 (2023) [PRX Quantum, in press]

    [4] I. Pogorelov, F. Butt et al., Experimental fault-tolerant code switching, arXiv:2403.13732 (2024)

  • Tobias Haug (Quantum Research Center, TII, Abu Dhabi):

    Efficient Algorithms for Quantum Magic

    Nonstabilizerness or magic characterizes the resources needed to run fault-tolerant quantum computers and is a necessary condition for quantum advantage. The resource theory of magic quantifies the amount of magic in quantum states, which characterizes the cost of preparing states on quantum computers as well as the runtime of a class of classical simulation algorithms. Here, we provide efficient algorithms to quantify magic on quantum computers [1,2] and matrix product states [3,4]. We use these methods to experimentally study the transition from classically simulable stabilizer states into intractable quantum states, and demonstrate their application for state discrimination and certification. Our work also gives novel insight into the magic of critical many-body quantum systems. We reveal that stabilizer entropy, a measure of nonstabilizerness, is in general not extremal even at the critical point. We show that stabilizer entropies can be used to determine the critical point of the transverse field Ising model, and find evidence of magic becoming long-range close to the critical point. Our works open up the exploration of quantum complexity in many-body quantum systems and quantum computers.

  • Chandrashekar Radhakrishnan (NYU Shanghai):

    Generalization of Quantum Discord

    An important aim of quantum information theory is to understand and quantify the various quantum properties and correlations. This is done by constructing measures and in understanding the operational relevance of information theoretic quantities. The best-known measure of nonclassical correlations is quantum discord [1,2]. In this talk, I will introduce a generalisation of quantum discord to multipartite systems using quantum conditional mutual information [3]. For the tripartite case, we show that the discord can be decomposed into contributions resulting from changes induced by nonclassical correlation breaking measurements in the conditional mutual information and tripartite mutual information. I will also discuss its relation to bipartite nonclassical correlations and monogamy of nonclassical correlations.

  • Elio König (Max Planck Institute for Solid State Research):

    Zero Is Not Nothing

    The interplay of topological electronic band structures and strong interparticle interactions provides a promising path toward the constructive design of robust, long-range entangled many-body systems. Most recent theories unveil that non-trivial topology is crucially manifested in the zeros of the fermionic Green’s function in Mott insulating systems and demonstrate the occurrence of topological band structures of zeros, and – by bulk-boundary correspondence – of topological edge states of zeros [1]. In this talk, I will spend some time reviewing topological Green’s function zeros and discussing their physical meaning and potential ways to probe them. I will then spend most of the time presenting an exactly soluble local model Hamiltonian [2] based on the Toric Code coupled to fermionic degrees of freedom. I’ll demonstrate the appearance of Green’s function zeros in a non-trivial, integrable limit of the model and employ controlled perturbation theory to demonstrate their topological band structure. I’ll further show that, within this model, Green’s function zeros acquire a finite ‘’lifetime’‘ before the Higgs transition, at which they disappear. The local nature of the model allows us to straightforwardly calculate the quantized Hall response.

    [1] N. Wagner, …, EJK, …, G. Sangiovanni, Nat Commun 14, 7531 (2023).

    [2] S. Bollmann, C. Setty, U. Seifert, EJK arXiv:2312.14926

  • Aditi Mitra (NYU New York):

    Topological Defects in Floquet Circuits

    I will discuss how one may construct Floquet models from a fusion category, and how this formalism is a natural way to construct topological defects: non-local operators that can be deformed in the space and time direction without changing the physics. One of these topological defects is the “duality defect” that implements the Kramers-Wannier duality transformation and is a “non-invertible symmetry” as it projects out states of a given parity. I will highlight the consequence of the duality defect on Floquet time-evolution, first for the exactly solvable Floquet-Ising model, and then by adding integrability breaking perturbations to the model.

  • Nadia Boutabba (Institute of Applied Technology, FCHS):

    Optically Dense Atomic Systems: From Pulse Shaping to Atomic Localization via Mangneto Optical Rotation

    The quantum control of atomic systems can be achieved through the manipulation of their optical properties, i.e the coherence. In EIT systems, a transparency window is achieved via the interference of two laser beams. In this context, our research investigates shaped laser wave-forms to obtain desirable absorption dispersion spectra, controllable refractive index and induces the atomic population inversion. For instance, q-deformed hyperbolic pulse manipulates the system’s dynamic by adjusting the scaling asymmetry factor q of the q-deformed pulse. In addition, the QEXP pulse opens a transparency window in the absorption spectra. In contrast, in the classical scenario where the laser is non-shaped, we control the optical properties of atomic systems via the SGC: spontaneously generated coherence or the MOR.

  • Ken Shiozaki (Yukawa Institute for Theoretical Physics, Kyoto University):

    A Discrete Formulation of Three Dimensional Winding Number

    For a continuous map from a three-dimensional oriented closed manifold to U ( N ) U(N) , the group of NN by NN unitary matrices, an integer-valued quantity known as the three-dimensional winding number is defined. We discuss a method to compute the winding number using a discrete approximation of the manifold, ensuring that the result is manifestly quantized. Our approach is a three-dimensional analog of the Fukui-Hatsugai-Suzuki method for calculating the first Chern number.

  • Asif Equbal (NYU AD):

    Quantum Vision for Health: Pioneering Light-Activated Spin Sensing

  • Frederico Brito (Quantum Research Center, TII, Abu Dhabi):

    Experimental Investigation of Geometric Quantum Speed Limits in Open Quantum Systems

    The Quantum Speed Limit (QSL) is a fundamental lower bound on the evolution time for quantum systems undergoing general physical processes and may have important consequences for quantum computing. Here, we study the geometric quantum speed limits of a qubit subject to decoherence in an ensemble of chloroform molecules in a Nuclear Magnetic Resonance experiment. To do so, we controlled the system-reservoir interaction and the spin relaxation rates by adding a paramagnetic salt, which allowed us to observe both Markovian and non-Markovian open system dynamics for the qubit. We used two distinguishability measures of quantum states to assess the speed of the qubit evolution: the quantum Fisher information (QFI) and Wigner-Yanase skew information (WY). We observed crossovers between QSLs related to the QFI and WY metrics for non-Markovian dynamics and low salt concentrations. The WY metric sets the tighter QSL for high concentrations and Markovian dynamics. We also show that QSLs are sensitive even to small fluctuations in spin magnetization.

  • Urs Schreiber (NYU AD):

    Towards Certified Topological Quantum Programming via Linear Homotopy Types

    Beyond the present NISQ era, useful heavy-duty quantum programs will arguably necessitate (1.) topological quantum circuits for error-protection and (2.) (classical-)computer-verified certificates of correctness — hence essentially a formal verification logic of the underlying topological quantum processes — which may seem a tall order. But we have recently shown that the (conservative) extension of the (programming & certification-)language of “Homotopy Type Theory” (HoTT) by “linear homotopy types” (LHoTT, for which prototypes exist on paper) namely: by classically-controlled topological quantum data types, naturally lends itself to just this purpose. In this talk I will give an introduction to and survey of this approach to Topological Quantum Programming Certification via Linear Homotopy Types, developed at CQTS @ NYUAD (“Topological Quantum Gates in HoTT” arXiv:2303.02382, “Entanglement of Sections” arXiv:2309.07245, “The Quantum Monadology” arXiv:2310.15735, “Quantum and Reality” arXiv:2311.11035).


Oct 2024

03 Oct 2024

NYU CQTS X QinnovisionQuantum Computing Workshop – PlanQK platform training


Talks:

  • Enrique Solano (Kipu Quantum, Berlin, Germany):

    Strategic Overview: Quantum Computing in the next Decade

  • Daniel Voltz:

    Quantum Computing in Action: Cutting-Edge Applications for Industry Pioneers

  • Michael Falkenthal:

    Advanced Quantum Applications: Real-World Use Cases on Kipu Quantum’s Platform


04 Oct 2024

Quantum Industry Day – Towards Industrial Usefulness with Kipu Quantum

www.q-innovision.com/quantum-industry-day


Nov 2024

19 Nov 2024

Quantum Industry Day – Exploring Quantum Frontiers with IBM Quantum Technology

www.q-innovision.com/quantum-industry-day-november-2024-ibm


23-24 Nov 2024

MENA Quantum Conference 2024

nyuad.nyu.edu/en/events/2024/november/mena-quantum.html


Dec 2024

16 Dec 2024

Quantum Industry Day – IDQUantique

www.q-innovision.com/quantum-industry-day-idq-december


Jan 2025

15 Dec 2025

Quantum Industry Day – Exploring Quantum with Qibo

www.q-innovision.com/quantum-industry-day-january-2025-tii


Feb 2025

28 Feb 2025

Quantum Industry Day Featuring Microsoft

www.q-innovision.com/quantum-industry-day-featuring-microsoft


Apr 2025

17 Apr 2025

Quantum Industry Day

www.q-innovision.com/quantum-industry-day-april-2025



May 2025

Program:

−−−−−−−−−−−\phantom{-----------}Monday, May 19:

TimeSpeaker
08:00-08:45[Breakfast]
09:00-09:45Javad Shabani (NYU)
09:50-10:35Meng Cheng (Yale)
10:35-11:00[Break]
11:00-11:45Sankar Das Sarma (University of Maryland)
11:45-13:00[Lunch]
12:00-13:45Sophia Economou (Virginia Tech)
13:50-14:35Tudor Stanescu (West Virginia)
14:35-15:00[Break]
15:00-15:45Abhay Pasupathy (Columbia University)
15:50-16:35Yi Li (Johns Hopkins University)
16:35-17:00[Break]
17:00-18:00Chetan Nayak (Microsoft)
18:00[Dinner]


−−−−−−−−−−−\phantom{-----------}Tuesday, May 20

TimeSpeaker
08:00-08:45[Breakfast] −−−−−−−−−−−−−\phantom{-------------}
09:00-9:45Hisham Sati (NYU Abu Dhabi)
09:50-10:35Tim Byrnes (NYU Shanghai)
10:35-11:00[Break]
11:00-11:45Pouyan Ghaemi (CUNY)
11:45-13:00[Lunch]
13:00-13:45Emil Prodan (Yeshiva University)
13:50-14:35Nicolas Regnault (Princeton University)
14:35-15:00[Break]
15:00-15:45Urs Schreiber (NYU Abu Dhabi)
15:50-16:35Andrei Vrajitoarea (NYU New York)
17:00[Closing]


Group photo:


Titles and materials:


  • Meng Cheng:

    Anomalous Insights into Phases of Matter in Open Quantum Systems


  • Sankar Das Sarma:

    Majorana Nanowires in Semiconductor/Superconductor Hybrid Platform




  • Abhay Pasupathy:

    Some thoughts on disorder in superconductors relevant to qubits




  • Hisham Sati:

    Global perspectives on topological quantum matter/information



  • Pouyan Ghaemi:

    Quantum algorithm to realize and study fractional Hall states and their dynamics on near term quantum computers: A tabletop experiment on quantum gravity





  • Andrei Vrajitoarea:

    Quantum-controlled Synthetic Matter:
    when analog and digitial hybridize



Quantum Colloquium

Weekly colloquium, broadly on quantum systems, with focus on quantum computation and specifically on topological quantum computation and dependently typed quantum programming languages.


May 2022


Sep 2022





Oct 2022



Nov 2022




  • 21 Nov 2022

    Andrew Kent (Center for Quantum Phenomena, NYU)

    A new spin on magnetism with applications in information processing

    slides: pdf

    video: rec, YT

    Recent advances in magnetism research are likely to have an important impact on electronics and information processing. These advances use the electron magnetic moment (spin) to transmit, write and store information. They enable new devices that operate at high speed with very low energy consumption. The information is stored in the orientation of electron magnetic moments in magnetic materials and can persist without power; energy is only needed to write and read the information. Important physics concepts include the interconversion of electrical (charge) currents into spin currents, the efficiency of the interconversion, controlling the currents, spin polarization direction, and the associated spin torques on magnetic order. Magnetic skyrmions are also of interest both because of their stability — they are topologically protected objects — and because their nucleation and motion can be controlled using spin currents. In this talk I will highlight the new physics concepts that have enabled these advances and discuss some of their applications in information processing.

cf.: J. Appl. Phys. 130 (2021) [doi:10.1063/5.0046950]



Dec 2022


  • 12 Dec 2022

    Leandro Aolita

    Quantum Algorithms, from noisy intermediate scale devices through the early fault-tolerant era

    video: rec, YT

    Reaching long-term maturity in quantum computation science and technology relies on the field delivering practically useful application in a short term. In this colloquium, I will discuss ideas for the noisy intermediate scale (NISQ) and early fault-tolerant eras. I will divide my talk into two parts. In the first part, I will make a brief non-technical introduction to the field, its relevance to the UAE, and the main lines of research of the Quantum Algorithms division at QRC-TII.

    In the second one, I will try to convey some level of technical detail about our work. In particular, I will first present a hybrid classical-quantum algorithm to simulate high-connectivity quantum circuits from low-connectivity ones. This provides a versatile toolbox for both error-mitigation and circuit boosts useful for NISQ computations. Then, I will move on to algorithms for the forthcoming quantum hardware of the early fault-tolerant era: I will present a new generation of high-precision algorithms for simulating quantum imaginary-time evolution (QITE) that are significantly simpler than current schemes based on quantum amplitude amplification (QAA). QITE is central not only to ground-state optimisations but also to partition-function estimation and Gibbs-state sampling, with a plethora of computational applications.


Jan 2023

  • 30 Jan 2023

    Vivek Singh (CQTS @ NYU Abu Dhabi)

    Chern-Simons theory, Knot polynomials & Quivers

    slides: pdf

    video: rec, YT

    cf. arXiv:2103.10228

    First, I will give a brief introduction to knot theory and its connection to Chern-Simons quantum field theory. Then I discuss the method of obtaining polynomial invariants and limitations towards tackling classification of knots. In particular, we will highlight our new results on weaving knots and review the recent developments on Knot-Quiver correspondence.


Feb 2023

  • 13 Feb 2023

    Kazuki Ikeda (Co-design Center for Quantum Advantage, Stony Brook University, USA)

    Demonstration of Quantum Energy Teleportation by Superconducting Quantum Processors and Implications for Communications and High Energy Physics

    Quantum energy teleportation is a theoretical concept in quantum physics that describes the transfer of energy from one location to another without the need for a physical medium to carry it. This is made possible by means of universal properties of quantum entanglement and measurement of quantum states. The role of QET in physics and information engineering is largely unexplored, as the theory has not received much attention for long time since it was proposed about 15 years ago. To validate it on a real quantum processor, my research has tested the energy teleportation protocol in its most visible form for the first time on IBM’s superconducting quantum computer. In my colloquium talk, I will explain the historical background of quantum energy teleportation, quantum circuits and quantum operations. Moreover I will present a concrete setup for a long-distance and large-scale quantum energy teleportation with real quantum networks.

    In addition, I will present the results of quantum simulations with relativistic field theory as a study based on the high-energy physics perspective and the symmetry-protected topological (SPT) phase of matter of quantum energy teleportation. The models will describe include the two dimensional QED (the massive Thirring model), the AKLT model, the Haldane model, and the Kitaev model. Those results show that the phase diagrams of the field theory and SPT phase are closely related to energy teleportation.

    In summary my talk will provide a novel suggestion that quantum energy teleportation paves a new pathway to a link between quantum communication on real quantum network, phase diagram of quantum many-body system, and quantum computation.



  • 27 Feb 2023

    Aeysha Khalique (National University of Science and Technology, Islamabad):

    Computational Tasks through Non-Universal Quantum Computation

    video: YT

    Quantum Mechanics offers phenomena which defy our everyday observation. These are not just theoretical principles but have wide range applications in quantum computation and quantum information, making some tasks possible which are impossible to be done classically. This talk will take you to the journey through quantum computation, starting from underlying principles to the applications, including my own own contribution to it.


Mar 2023


  • 6 Mar 2023

    Altaf Nizamani and Qirat Iqbal (University of Sindh, Pakistan):

    Quantum Technology with Trapped Ions

    video: YT

    Quantum technology is a rapidly advancing field that is poised to revolutionize numerous industries, including computing, communications, sensing, and cryptography. At its core, quantum technology relies on the principles of quantum mechanics, which allow for the creation of devices that operate on the quantum level. These devices based on quantum technology can perform tasks that are impossible or prohibitively difficult for classical devices. One of the most promising applications of quantum technology is in quantum computing, quantum communications, and quantum sensors.

    Trapped ions are one of the promising platform for quantum computing and sensing. In this approach, individual ions are trapped in a vacuum chamber using electromagnetic fields and manipulated using lasers to perform quantum operations. As a quantum system, trapped ions offer several advantages. First, they have long coherence times, meaning that the quantum state of the ion can be preserved for a longer period, allowing for more complex calculations. Second, trapped ions can be precisely controlled and manipulated, allowing for the implementation of high-fidelity quantum gates. Finally, trapped ions can be entangled with one another, allowing for the implementation of quantum algorithms that are impossible to simulate on classical computers. Trapped ions also have great potential as quantum sensors. By using the properties of the ions to measure changes in their environment, trapped ions can detect minute changes in temperature, magnetic fields, and electric fields, among other things. This makes them useful for applications in precision measurement, such as in atomic clocks, gravitational wave detection, and magnetometry.

    One of the major challenges facing trapped ion systems is scalability. While individual ions have been used to perform simple quantum algorithms, scaling the system up to include a large number of ions is a difficult task. However, recent advances in ion trap technology have made it possible to trap larger numbers of ions and transport them in 2D and 3D space to perform more complex operations for quantum computation and sensing experiments. Realization of such devices is not far away. As compared to present atomic clocks, a new generation of quantum-enhanced clocks is now emerging showing significantly improved accuracy. Sensitive physical measurements are an essential component of modern science and technology. Developments in quantum sensors will outdate their classical counterparts.

    We will present recent developments and opportunities in quantum technology applications based on trapped ions, including quantum computation and sensing.


  • 13 Mar 2023

    Roger S. K. Mong (Pittsburgh Quantum Institute, USA)

    Detecting topological order from modular transformations of ground states on the torus

    cf.: arXiv:2203.04329

    Every two-dimensional topological phase is associated with some topological quantum field theory (TQFT), or more formally a modular tensor category. The ground states of a topological phase encode information about the TQFT, which makes them useful in determining the TQFT data, such as anyon mutual statistics and self statistics. For example, many numerical methods for detecting the TQFT relied on the use of minimum entanglement states (MESs), which are the eigenstates of the Wilson loop operators, and are labeled by the anyons corresponding to their eigenvalues. Here we revisit the definition of the Wilson loop operators and MESs. We rederive the modular transformation of the ground states purely from the Wilson loop algebra, and as a result, the modular SS- and TT-matrices naturally show up in the overlap of MESs. Importantly, we show that due to the phase degree of freedom of the Wilson loop operators, the MES-anyon assignment is not unique. This ambiguity means that there are some sets of TQFTs that cannot be distinguished from one another solely by the overlap of MESs.


  • 27 Mar 2023

    Matthias Christandl (Centre for the Mathematics of Quantum Theory, U. Copenhagen):

    Quantum Software

    cf.: arXiv:2009.07161 doi:10.1109/TIT.2022.3169438

    In these days, we are witnessing amazing progress in both the variety and quality of platforms for quantum computation and quantum communication. Since algorithms and communication protocols designed for traditional ‘classical’ hardware do not employ the superposition principle and thus provide no gain even when used on quantum hardware, we are in need of developing specific quantum algorithms and quantum communication protocols that make clever use of the superposition principle and extract a quantum advantage. “Quantum hardware needs quantum software”, so to say. Furthermore, due to noise in the qubits, known as decoherence, an additional quantum-specific software layer is required that emulates a perfect quantum machine on top of a noisy one. I will demonstrate our recent work on this subject with theorems as well data from university and commercial quantum devices.


Apr 2023

  • 3 Apr 2023

    Mouzhe Xie (University of Chicago)

    Diamond-based quantum sensor for molecular analytics

    cf.: arXiv:2108.04843

    slides: pdf

    video: YT

    Quantum sensing technologies enable some of the most precise measurements that human beings have ever achieved. In recent years, optically addressable nitrogen-vacancy (NV) color center hosted by diamond crystal has been used as a novel quantum sensor, which has exquisitely sensitive response to local magnetic field fluctuations. It is therefore capable to perform micro-/nano-scale NMR experiments, manifesting enormous potential to study biological systems on extremely small sample volume – even down to single-molecule regime.

    In this seminar, I will discuss some of the comprehensive efforts to develop NV-based quantum sensing platforms for a wide range of applications in chemistry and biology. I will start with a general introduction to quantum sensing followed by conventional NMR spectroscopy as a powerful tool to study biomolecules, as well as their connections to the NV-based nanoscale NMR. I will then introduce a biocompatible surface functionalization architecture for interfacing a diamond quantum sensor with individual intact biomolecules under physiological conditions. A sensing modality based on diamond membrane integrated with flow channel will also be discussed, which is a promising platform for a variety of experiments a molecular, cellular, and even living-organism levels. Finally, I will conclude by providing an outlook on how NV-based quantum sensing platforms, combined with other advanced spectroscopy and microscopy methods, can be utilized to address important biophysical and bioanalytical questions with unprecedented sensitivity and spatial resolution, which will enhance our understanding of molecular interactions and cellular processes and ultimately improve human health.



  • 10 Apr 2023

    Zain Saleem (Argonne National Lab, USA)

    Classical simulators as quantum error mitigators via circuit cutting

    cf.: arXiv:2212.07335

    video: YT

    We introduce an error mitigation framework that mitigates errors in a quantum circuit using circuit cutting. Our framework can be implemented in polynomial time for a wide variety of quantum circuits. Our technique involves cutting the circuit in such a way that we run the circuit that needs to be executed on the quantum hardware whereas the error mitigation circuit is run on a simulator. We perform error mitigation qubit by qubit and then provide a way to combine the different probabilities from each of the individual qubit error mitigation runs such that the full circuit is error mitigated. We apply our framework to the VQE hardware-efficient ansatz acheiving estimated ground state energies very close to the noise-free simulation results.



  • 24 Apr 2023

    Mauro Paternostro (Queen’s University Belfast, Ireland):

    Alice through the looking glass: cavity optomechanics for the study of the foundation of quantum mechanics

    cf.: arXiv:2302.08995

    I will illustrate how cavity optomechanics is helping us addressing deep questions on our understanding of the foundations of quantum theory, from non-equilibrium quantum dynamics to the collapse of the wave-function. Towards the end of my talk, I will propose an optomechanical pathway for the exploration of the potential quantum nature of gravity.


May 2023


  • 1 May 2023

    Hichem El Euch (American University of Sharjah, UAE):

    High-fidelity universal quantum computation with symmetric qubit clusters

    Designing a physical device that maintains the error rate for each quantum processing operation low is one of the most arduous issues for the implementation of a scalable quantum computer. These errors may result from inaccurate quantum manipulation, such as a gate voltage sweeping in solid-state qubits or a laser pulse duration. Decoherence is usually a manifestation of the interaction with the environment, and it is an entity of the quantum system which generates errors. Small clusters of qubits with symmetries can be used to shield part of them from decoherence. We encode pairs of connected qubits and universal 2-qubit logical gates using 4-level cores with omega-rotation invariance. We show that symmetry renders logical operations particularly resistant to anisotropic qubit rotations that models some quantum errors. We suggest a scalable method for universal quantum processing in which cores act as quansistors, or quantum transistors. By adjusting their intrinsic variables, quansistors may be dynamically isolated from their environment, providing them the adaptability needed to function as controlled quantum memory units.


  • 8 May 2023

    Ilya Kuprov (University of Southampton):

    Optimal control of large spin systems

    cf.: arXiv:2107.00933, arXiv:2303.09458

    video: YT

    In magnetic resonance, optimal control theory is used to generate pulses and pulse sequences that achieve instrumentally difficult objectives (for example, uniform 13C excitation in a 1.2 GHz magnet) with high precision under stringent time and radiofrequency/microwave power constraints. At the moment, the most popular framework is GRAPE (gradient ascent pulse engineering, 10.1016/j.jmr.2004.11.004). This lecture reports our recent mathematical and software engineering work on the various extensions and refinements of the GRAPE framework, and on its implementation as a module of Spinach library. Recently implemented functionality includes: fidelity Hessians and regularised Newton-Raphson optimisation, generalised curvilinear waveform parametrisation, prefix and suffix pulse sequences, multi-target and subspace control, keyhole states and subspaces, cooperative pulses and phase cycles, and piecewise-linear control sequences. In keeping with the long tradition, the methods are also directly applicable to quantum technologies outside Magnetic Resonance.


Sep 2023


Oct 2023

  • 2 Oct 2023

    Titus Neupert (University of Zurich)

    Realizing Higher-Order Topology

    video: Zm

    cf. doi:10.1126/sciadv.aat0346

    Higher-order topology generalizes the bulk-boundary correspondence of topological phases of matter, by allowing topological modes to be localized at corners and hinges instead of edges and surfaces. I will introduce the theory behind this concept, both for noninteracting as well as interacting systems and consecutively discuss two realizations in rather distinct setups. First, as-grown crystals of bismuth, grey arsenic, as well as bismuth bromide are demonstrated to display the essential physics of higher-order topological insulators. Second, it is shown that lattices of so-called Shiba bound states induced by magnetic adatoms in conventional superconductors can be brought into a higher-order superconducting phase. I will report on experimental progress for both system types based on spanning probe as well as transport measurements.



  • 16 Oct 2023

    Anne Broadbent (University of Ottowa, Canada)

    Quantum Delegation with an Off-the-Shelf Device

    video: Zm

    cf. arXiv:2304.03448

    Given that reliable cloud quantum computers are becoming closer to reality, the concept of delegation of quantum computations and its verifiability is of central interest. Many models have been proposed, each with specific strengths and weaknesses. Here, we put forth a new model where the client trusts only its classical processing, makes no computational assumptions, and interacts with a quantum server in a single round. In addition, during a set-up phase, the client specifies the size nn of the computation and receives an untrusted, off-the-shelf (OTS) quantum device that is used to report the outcome of a single constant-sized measurement from a predetermined logarithmic-sized input. In the OTS model, we thus picture that a single quantum server does the bulk of the computations, while the OTS device is used as an untrusted and generic verification device, all in a single round. In this talk, we will show how the delegation of quantum computations can be achieved in the OTS model, and furthermore how to make this protocol zero-knowledge. The emphasis will be on the concepts that contribute to this result; these concepts are drawn from a long line of research related to blind and delegated quantum computation, as well as quantum zero-knowledge proofs. Based on joint work with Arthur Mehta and Yuming Zhao.


  • 23 Oct 2023

    Frank (Peng) Fu (Univ. Soth Carolina):

    Proto-Quipper with Dynamic Lifting

    video: YT, Zm

    Quipper is a functional programming language for quantum computing. Proto-Quipper is a family of languages aiming to provide a formal foundation for Quipper. By virtue of being a circuit description language, Proto-Quipper has two separate runtimes: circuit generation time and circuit execution time. Values that are known at circuit generation time are called parameters, and values that are known at circuit execution time are called states. Dynamic lifting is an operation that enables a state, such as the result of a measurement, to be lifted to a parameter, where it can influence the generation of the next portion of the circuit. As a result, dynamic lifting enables Proto-Quipper programs to interleave classical and quantum computation. In his talk, Dr. Frank will describe how to extend Proto-Quipper-M with dynamic lifting. He will explain the syntax of a language named Proto-Quipper-Dyn. Its type system uses a system of modalities to keep track of the use of dynamic lifting. Then, he will discuss the categorical semantics for dynamic lifting. Finally, if time permits, Dr. Frank will give some examples of Proto-Quipper-Dyn programs.



Nov 2023

  • 06 Nov 2023

    Alberto Marchisio (NYUAD):

    Quantum Machine Learning: Current Trends, Challenges, Opportunities, and the Road Ahead

    video: Zm

    cf. arXiv:2310.10315

    Quantum Computing (QC) claims to improve the efficiency of solving complex problems, compared to classical computing. When QC is applied to Machine Learning (ML) applications, it forms a Quantum Machine Learning (QML) system. After discussing the basic concepts of QC and its advantages over classical computing, this talk reviews the key aspects of QML in a comprehensive manner. We discuss different QML algorithms and their domain applicability, quantum datasets, hardware technologies, software tools, simulators, and applications. Valuable information and resources are provided to jumpstart into the current state-of-the-art techniques in the QML field.


Dec 2023


  • 11 Dec 2023

    Chandrasekhar Ramanathan (Dartmouth College, New Hampshire):

    Quieting Noisy Neighbors: Extending the Coherence Times of Central Electronic Spins in Solids

    video: YT

    cf.: arXiv:arXiv:2311.05396

    Isolated electronic spins such as donors in silicon and defects like the nitrogen-vacancy (NV) center in diamond are promising platforms for some quantum technologies. The decoherence of these spins is often dominated by interactions with other electronic or nuclear spin species present in their vicinity. For example, silicon-29 nuclear spins can limit the coherence times of donors in silicon, and substitutional nitrogen or P1 centers often limit the coherence times of NV centers in diamond. In this talk I will describe two recent sets of experiments from our group where we are able to extend the coherence times of the central spin by engineering these spin-bath interactions. First, I show how the coherence times of phosphorus donors in silicon are influenced by low-power above-bandgap optical excitation. Next, I describe the use of dynamical decoupling techniques to suppress NV-P1 interactions in diamond. In addition to extending coherence times, these decoupling techniques can be used to measure time-dependent magnetic fields, a form of AC-sensing or noise spectroscopy.


Jan 2024


  • 28 Jan 2024

    Alessandra Di Pierro (University of Verona):

    Topological Kernels via Quantum Computation

    cf. arXiv:2307.07383

    Topological data analysis (TDA) enhances the analysis of objects by embedding them into a simplicial complex and extracting useful global properties such as the Betti numbers, i.e. the number of multidimensional holes, which can be used to define kernel methods that are easily integrated with existing machine-learning algorithms. These kernel methods have found broad applications, as they rely on powerful mathematical frameworks which provide theoretical guarantees on their performance. However, the computation of higher-dimensional Betti numbers can be prohibitively expensive on classical hardware, whereas quantum algorithms can approximate them in polynomial time in the instance size. In this work, we propose a quantum approach to defining topological kernels that is based on constructing Betti curves, i.e. topological fingerprint of filtrations with increasing order.


Feb 2024

  • 05 Feb 2024

    Julien Ross:

    Catalytic Embeddings: Theory and Applications

    cf.: arXiv:2305.07720

    video: kt

    Let CC be a quantum circuit and let GG be a set of quantum gates. A catalytic embedding of CC over GG is a pair (D,v)(D,v) consisting of a state vv and a circuit DD over GG such that for every state uu we have D(u⊗v)=(Cu)⊗vD(u \otimes v) = (C u) \otimes v. Because the state vv is left unchanged by the application of DD, it is known as a catalyst. Catalytic embeddings are useful when the circuit CC cannot be exactly represented over the gate set GG. In such cases, one can leverage the catalyst to implement (any number of occurrences of) CC using circuits over GG.

    In this talk, I will present the theory of catalytic embeddings and discuss applications to the exact and approximate synthesis of quantum circuits.


  • 12 Feb 2025

    Chandrashekar Radhakrishnan (NYU Shanghai):

    Theory of Quantum Coherence and Its Application in Quantum Synchronization

    video: Zoom

    Coherence is a well-known feature of quantum systems. An information theoretic investigation of quantum coherence was initiated in [1] from a resource theory perspective. In this talk, I will provide an outline of quantifying coherence, the two different forms corresponding to it namely the intrinsic coherence and local coherence, and trade-off relation between these two types of coherence [2]. As an application, I will talk about the role of quantum coherence in the study of quantum synchronization. First, I will give an overview of synchronization. Then considering an open quantum system comprising of a two-level system interacting with an external environment, I will show how it exhibits phase preference in the long-time limit. While this phase preference, which we identify as quantum phase localization, shows features like Arnold tongue, which is considered as an identifier for quantum synchronization, I present evidence to show that it is not quantum synchronization [3]. Finally, I will discuss the challenges remaining to be addressed in connecting these two related phenomena of quantum phase localization and quantum synchronization.

    References:

    1. T. Baumgratz, M. Cramer, M. B. Plenio, Quantifying Coherence, Phys. Rev. Lett. 113 140401 (2014) [arXiv:1311.0275, doi:10.1103/PhysRevLett.113.140401]
    2. R. Chandrashekar, P. Manikandan, J. Segar, Tim Byrnes, Distribution of quantum coherence in multipartite systems, Phys. Rev. Lett. 116 150504 (2016) [arXiv:1602.00286, doi:10.1103/PhysRevLett.116.150504]
    3. Md. Manirul Ali, Po-Wen Chen, R. Chandrashekar, Physica A 633, 129436 (2024) [doi:10.1016/j.physa.2023.129436]


  • 19 Feb 2024

    Venkata SubbaRao Redrouthu (NYU AD):

    The Quantum Symphony: Electron Spin Choreography for Hyperpolarized Nuclear Spin Sensing

    Delving into the atomic secrets encoded within nuclear spins necessitates a quantum leap in sensitivity. My research endeavors to achieve this leap through Pulsed Dynamic Nuclear Polarization (DNP), an emerging technique that harnesses quantum-controlled electron spins to hyperpolarize nuclear spins, overcoming inherent sensitivity challenges in Nuclear Magnetic Resonance (NMR) spectroscopy.

    In this presentation, I demonstrate a novel quantum mechanical scheme: broad-band pulsed DNP sequences. Comprising carefully choreographed sequences of quantum gates or pulses, each precisely controlled in phase and time, these sequences represent a pivotal advancement beyond conventional DNP methods. Through density matrix-based theoretical analyses and numerical simulations, I navigate the intricacies of these sequences, offering a deeper comprehension of their foundational principles and the quantum symphony they orchestrate in enhancing nuclear spin sensitivity.


  • 26 Feb 2024

    Benoît Valiron:

    Reversible and Quantum Control-Flow

    video: zm, kt

    cf. arXiv:1804.00952

    One perspective on quantum algorithms is that they are classical algorithms having access to a special kind of memory with exotic properties. This perspective suggests that, even in the case of quantum algorithms, the control flow notions of sequencing, conditionals, loops, and recursion are entirely classical. There is, however, another notion of execution control flow that is itself quantum. In this talk, we shall overview the two paradigms and discuss the issues specific to quantum control.


Mar 2024

  • 08 Mar 2024

    Hayder Salman (University of East Anglia):

    Dynamics of a Nonequilibrium Discontinuous Quantum Phase Transition in a Spinor Bose-Einstein Condensate

    cf. arXiv:2312.16555

    video: Zoom

    Symmetry-breaking\;quantum phase transitions lead to the production of topological defects or domain walls in a wide range of physical systems. In second-order transitions, these exhibit universal scaling laws described by the Kibble-Zurek mechanism, but for first-order transitions a similarly universal approach is still lacking. Here we propose a spinor Bose-Einstein condensate as a testbed system where critical scaling behavior in a first-order quantum phase transition can be understood from generic properties. We generalize the Kibble-Zurek mechanism to determine the critical exponents for: (1) the onset of the decay of the metastable state on short times scales, and (2) the number of resulting phase-separated ferromagnetic domains at longer times, as a one-dimensional spin-1 condensate is ramped across a first-order quantum phase transition. The predictions are in excellent agreement with mean-field numerical simulations and provide a paradigm for studying the decay of metastable states in experimentally accessible systems.


  • 25 Mar 2024

    Kapil Kumar:

    Realization and Characterization of Topological Materials

    Topological insulators (TIs) have emerged as a fascinating class of materials with unique electronic properties driven by non-trivial topology. Their exotic behavior, such as robust metallic states on the surface while being insulating in the bulk, has attracted significant attention from both theoretical and experimental communities. Characterizing these materials accurately is crucial for understanding their fundamental properties and exploring potential applications in quantum computing, spintronics, and topological quantum devices.

    This abstract provides an overview of the characterization techniques employed in the study of topological insulators. We discuss both experimental and theoretical approaches utilized to probe their electronic structure, surface states, topological invariants, and transport properties. Experimental techniques encompass a wide range of methods, including angle-resolved photoemission spectroscopy (ARPES), scanning tunneling microscopy/spectroscopy (STM/STS), magneto-transport measurements, and optical spectroscopy. These techniques provide invaluable insights into the band structure, Fermi surface topology, surface states, and the presence of any exotic quantum phenomena.

    On the theoretical front, available various computational methods, such as density functional theory (DFT), tight-binding models, and topological indices, play a pivotal role in predicting and understanding the topological properties of these materials. These theoretical approaches not only aid in interpreting experimental results but also guide the design of novel topological materials with tailored properties.

Apr 2024

  • 15 Apr 2024

    Elisa Ercolessi (University of Bologna, Italy):

    Hybrid Variational Algorithms on a Neutral Atom Platform

    Quantum Computing is seen as a potential breakthrough for the study of hard classical problems as well as for quantum many body systems. However, we are in the era of NISQ devices and still far away from fault-tolerant machines.

    This leads us to consider the possibility of hybrid classical-quantum protocols of variational type: they exploit quantum resources to efficiently prepare states that depend on a suitable chosen set of variational parameters, which can then be determined by means of optimization algorithms to be run on a classical computer. The choice of such classical optimizer schemes is to be guided by compatibility requirements with respect to current available quantum platforms.

    To evaluate the feasibility of such an approach, we present an application of the Quantum Approximate Optimization Algorithm to a typical classical hard combinatorial problem, that has been emulated and tested on a real Rydberg atom quantum machine.

May 2024


Sep 2024

  • 02 Sep 2024

    Nouhaila Innan (CQTS, NYUAD):

    Quantum Machine Learning for Advanced AI: Development and Application Across Diverse Domains

    As the demand for more sophisticated computational tools grows, Quantum Machine Learning (QML) emerges as a potential solution, combining the strengths of Machine Learning (ML) and Quantum Computing (QC) to push the boundaries of what is computationally possible. This exploration takes a deep dive into advanced QML models, such as quantum neural networks, and provides an extensive overview of fundamental data encoding techniques essential for translating classical data into quantum states. Building on these foundational elements, Quantum Federated Learning (QFL) is introduced as a novel approach that enhances privacy and security in decentralized systems by integrating federated learning with quantum principles. The discussion also covers potential applications in finance and cybersecurity, showcasing the significant impact QML could have on these sectors. This talk highlights the considerable potential of QML as a key enabler of advanced artificial intelligence, emphasizing its role in driving innovation across various domains.


  • 09 Sep 2024

    Sajith Sadasivan (CQTS, NYUAD)

    Role of Quantum Coherences in Integrated Solid Effect DNP

    Quantum sensing using magnetic resonance techniques, such as Nuclear Magnetic Resonance (NMR), Magnetic Resonance Imaging (MRI), etc. utilizes the quantum properties of the nuclear spins to explore the structural and dynamical characteristics of molecules. This makes it a powerful tool for materials science, biomedical, and quantum technology applications. However, these techniques suffer from an inherent low signal sensitivity. A hyperpolarization method known as Dynamic Nuclear Polarization (DNP) enhances the sensitivity of NMR and MRI by transferring polarization from electron spins to nuclear spins. The traditional DNP methods face challenges in efficiently polarizing systems with broad Electron Paramagnetic Resonance (EPR) lines. To overcome this limitation, Integrated Solid Effect (ISE) DNP is widely used for improved polarization transfer efficiency. Despite its broad application, the role of quantum coherences in ISE DNP remains poorly understood. The quantum coherences generated during electron-nucleus Double-Quantum (DQ) and Zero-Quantum (ZQ) transitions are crucial for maximizing DNP efficiency. Using density matrix formalism, we provide a detailed analysis of quantum coherences in the ZQ and DQ subspaces, as well as the electron’s Single-Quantum (SQ) basis, revealing their impact on ISE DNP. Our findings offer new insights into utilizing room-temperature hyperpolarization in biomedical applications.



  • 30 Sep 2024

    Vladimir Korepin (Stony Brook University, USA):

    Lessons of Many-Body Quantum Mechanics for Circuit Design

    cf. arXiv:2406.08320

    slides: pdf

    Brick-wall circuits composed of the Yang-Baxter gates are integrable. It becomes an important tool to study the quantum many-body system out of equilibrium. To put the Yang-Baxter gate on the quantum computer, it has to be decomposed into the native gates of quantum computers. It is favorable to apply the least number of native two-qubit gates to construct the Yang-Baxter gate. We study the geometric representations of all XX-type braid gates and their corresponding Yang-Baxter gates via the Yang-Baxterization. We find that the braid and Yang-Baxter gates can only exist on certain edges and faces of the two-qubit tetrahedron. We identify the parameters by which the braid and Yang-Baxter gates are the Clifford gate, the matchgate, and the dual-unitary gate. The geometric representations provide the optimal decompositions of the braid and Yang-Baxter gates in terms of other two-qubit gates. We also find that the entangling powers of the Yang-Baxter gates are determined by the spectral parameters. Our results provide the necessary conditions to construct the braid and Yang-Baxter gates on quantum computers.


Oct 2024

  • 21 Oct 2024

    Sheng-Jie Huang (Oxford University and Max Planck Institute for the Physics of Complex Systems):

    Quantum Matter Through the Lens of Topological Holography

    cf. arXiv:2405.09611

    It is well known that symmetry offers valuable insights for organizing quantum phases of matter and leads to important physical consequences, such as [conservation laws]] and constraints on the low-energy dynamics of a quantum field theory.

    Recently, significant progress has been made in generalizing the concept of symmetry and exploring its connection to topological defects. In this talk, I will introduce a holographic principle for generalized symmetries, referred to as topological holography, which describes the generalized symmetry of a quantum system in terms of a topological order in one higher dimension.

    This framework decouples the topological data from the local dynamics of the theory and provides a unified description of symmetry and duality in both gapped and gapless phases of matter. Specifically, I will focus on various exotic quantum critical points and gapless phases in (1+1)d, including phase transitions between symmetry-protected topological (SPT) phases, symmetry-enriched quantum critical points, deconfined quantum critical points, and intrinsically gapless SPT phases.


  • 22 Oct 2024

    Phani Kumar Peddibhotla (Indian Institute of Science Education and Research, Bhopal, India):

    Quantum Sensing Using NV Centers in Diamond

    cf.: arXiv:1612.05325

    Diamond serves as an ideal crystalline host for a variety of point defects due to its exceptional qualities such as wide band gap, small spin-orbit coupling, and its availability in high-quality, isotopically purified single crystals. Among the possible defects, the nitrogen-vacancy (NV) defect, which is an optically active paramagnetic defect, has been extensively studied as its spin state can be optically initialized and measured at room temperature, and can be manipulated via electron spin resonance by microwave radiation.

    Owing to its unique properties, the NV center in diamond has been used to measure a number of physical quantities such as magnetic field, electric field, temperature, and stress/strain at ambient conditions [1, 2]. Consequently, NV quantum sensors have not only enabled the measurement of magnetic resonance from a single electron spin and a few nuclear spins [1], but also emerged as a spectroscopic tool for imaging the charge and strain environments intrinsic to the diamond lattice [3,4].

    In this talk, I’ll discuss our recent work on utilizing NV sensors for high-sensitivity scalar, vector, and zero-field magnetometry applications.

    References:

    1. R. Schirhagl et al, Annual Reviews in Physical Chemistry, 2014, 65, 83.

    2. P. Peddibhotla et al, Nano Letters, 2017, 17 (3), 1496

    3. T. Mittiga et al, Phys. Rev. Lett. 121, 246402 (2018).

    4. S. Kumar et al, 2023 Quantum Sci. Technol. 8 025011


Nov 2024


  • 11 Nov 2024

    Arthur Parzygnat (MIT, USA):

    A Spatiotemporal Extension of Density Matrices and Time-Reversal Symmetry for Measurements

    slides: pdf

    If a quantum state distributed over regions of space provides the expectation values of observables on those regions, what object provides the expectation values of observables measured sequentially in time? Such objects have recently been given a mathematically rigorous formulation and are called “states over time”. This formalism, together with the recent advances in categorical probability theory, has led to a notion of Bayes' rule in quantum theory. In this setting, Bayes' rule provides a method to calculate reverse processes that give rise to time-reversal symmetric expectation values of measurements. I will introduce these ideas, summarizing key concepts from references [1,2,3].

    [1] Parzygnat, Fullwood “From time-reversal symmetry to quantum Bayes’ rules” PRX Quantum 4, 020334 (2023) arXiv:2212.08088

    [2] Fullwood, Parzygnat “Operator representation of spatiotemporal quantum correlations” arXiv:2405.17555

    [3] Parzygnat, Fullwood “Time-symmetric correlations for open quantum systems” arXiv:2407.11123


Dec 2024

  • 09 Dec 2024

    Yingyi Huang:

    Search for Majorana Zero Modes in Full-Shell Hybrid Nanowires for Topological Quantum Computing

    cf.: arXiv:1904.13374

    Majorana fermions are fermions that were originally proposed in particle physics by Ettore Majorana and are characterized as being their own anti-particle. In condensed matter systems, Majorana quasiparticles occur as fractionalized excitations with an associated topologically protected degeneracy. In this talk, I will briefly review the basic concepts and recent developments in the study of Majorana zero modes in semiconductor-superconductor nanowires and FeFe-based superconductors, and discuss the possible quantum anomalous vortex and Majorana zero mode in full-shell hybrid nanowires.


Jan 2025

  • 27 Jan 2025

    Al-Amin Dhirani (University of Toronto, Canada):

    Nanostructures: Building Blocks for Materials and Devices Exhibiting Tunable Quantum Behaviour

    Many nanostructures can be fabricated with exquisite control over size, shape, and chemical composition. Such advances suggest an interesting opportunity: can we exploit this nanoscale control and fabricate bulk materials and devices with behaviour – potentially even quantum behaviour - that is tuned from the nanoscale up? In other words, can we “nanoengineer” quantum materials/devices? In this talk, I will describe examples showing that this is indeed possible. Using gold nanostructures and molecules as linkers, we have demonstrated materials that exhibit: an insulator-to-metal transition with varying linker molecule; the Kondo effect (delocalized – localize electrons hybridization) where the transition temperature that can be raised to above 220K by varying the nanostructure; and clear quantum particle-in-a-box, molecular wire transport where conductance increases with increasing molecule length (conductance of classical wires exhibit the opposite trend: conductance decreases with wire length). To further explore the potential role of hybridization at nanoscales, we developed a combined transistor – electrochemical cell device (“charge exchange transistor”) and found evidence that redox charge transfer in electrochemistry can occur through a 2-step mechanism involving a quantum transition state, proving a view of electrochemistry through a quantum lens. Our results highlight that nanostructured materials and devices are a promising platform for studying quantum phenomena with unprecedented control.


Feb 2025

  • 3 Feb 2025

    Wael Itani (Tandon School of Engineering, NYU):

    Towards a Quantum Algorithm for Lattice Boltzmann (QALB) Simulation with a Nonlinear Collision Term

    slides: pdf

    cf. arXiv:2304.05915

    The lattice Boltzmann method, a discrete velocity model for fluid dynamics, presents intriguing possibilities for quantum computation. This thesis develops three distinct approaches to quantum algorithms for lattice Boltzmann (QALB), each offering unique mathematical insights. First, we analyze the concurrent Carleman linearization of the collision and streaming, revealing how the nonlinear streaming operator maps to an infinite-dimensional linear system with exponentially suppressed truncation errors. Second, we construct the first completely unitary algorithm with a quantum linear embedding using bosonic operators and prove that the BGK collision operator’s symmetries enable its decomposition into Hermitian and constant non-Hermitian components. We show that embedding error is convergent for a general differential equation driven by a nonlinear polynomial. We demonstrate that while the quantum linear embedding achieves polylogarithmic scaling in spatial discretization, its gate complexity remains polynomial in Reynolds number. Finally, we explore quantum machine learning approaches to the collision operator, developing physics-informed quantum neural networks with embedded lattice Boltzmann symmetries. The quantum machine learning approach offers potential runtime advantages but requires significant improvements in training loss to handle physically relevant Reynolds numbers.


  • 10 Feb 2025

    Sam Bayliss (University of Glasgow):

    Optically Addressable Spin Qubits in Chemically Synthesized Molecules

    cf.: arXiv:2004.07998, arXiv:2402.07572

    Optically addressable spins are a promising platform for quantum technologies due to their ability to be readily prepared, coherently controlled, and read out—exemplified by remarkable demonstrations with solid-state defects. Molecular materials are also attractive for hosting analogous optical-spin interfaces, with their chemical tunability and ability to be integrated with other systems offering promising functionality. Such properties could be beneficial for quantum sensing where, for example, precise spatial control between sensor and target is desired. To realise the potential of molecular spins for applications such as quantum sensing, the key combination of coherent spin manipulation and optical readout is desirable, combining sensitive detection capabilities with versatile control methods. In addition, such capabilities would ideally be accessible at room temperature. In this talk, I will describe examples of such functionality—ground-state molecular spins which can be optically interfaced, and excited-state spins which can realise high-contrast optically detected coherent control at room temperature—and outline how such systems are attractive as chemically synthesised spin qubits for quantum sensing.


  • 17 Feb 2025

    Francesco Ciccarello (University of Palermo):

    Atom-photon bound states in modern quantum optics

    slides: pdf

    cf. arXiv:2402.10275, arXiv:2108.11963

    Following recent technological advancements in experimental platforms such as circuit QED and ultracold atoms, the last decade has seen a growing interest in atom-photon bound states, which typically arise when a qubit is coupled to an engineered photonic lattice. Such states are key to a number of interesting effects such as fractional decay and, most of all, decoherence-free dipole-dipole interactions with potential applications for quantum information processing tasks. Here, we will present a (hopefully friendly) introduction to such states and the physics they give rise to. In the final part of the talk, we will show their generalization to the case of so called giant atoms. A giant atom is a new emergent paradigm of quantum optics; it is an artificial emitter that can couple to the field non-locally and as such can no longer be modelled as point-like system like in traditional quantum optics.


Apr 2025

  • 7 Apr 2025

    Simon Devitt (University of Technology Sydney)

    Quantum communications networks are an important component in the quantum technology ecosystem. Currently in their infancy, quantum communication systems currently consist of point to point connections that are primary used for quantum key distribution protocols. Despite this infancy, there has been significant technological investment and progress, with several countries, most notably the Chinese, launching successful satellite systems demonstrating both Quantum Key Distribution and entanglement distribution over distances up to 1,200km1,200 km. Despite these achievements, the theoretical design and experimental construction of a quantum network that would mimic the distance and speed performance of the classical internet has been elusive. Specifically, the network performance of quantum repeater or quantum satellite systems, even under optimistic engineering assumptions, would be orders of magnitude worse than the classical internet, precluding the development of a quantum internet that would augment, or perhaps in the future, replace the current classical internet.

    Our solution is a quantum variant of the sneakernet principle of network design. A downside of classical sneakernets is the issue of information latency. If the shipping route, for example, takes days, in not weeks, to transfer information from source to receiver then there is a significant latency between when the information is loaded onto a memory unit and when it is read out at the receiving end. In contrast, a quantum sneakernet does not suffer from significant latency on information transfer. Unlike a classical sneakernet, a quantum sneakernet does not transfer actual information. Instead, a quantum sneakernet distributes a quantum resource that can later be used for information teleportation protocols. Hence, this resource state is distributed slowly, offline, before any information is transmitted. We essentially prepare a virtual quantum “information pipeline” using sneakernet principles which can then be consumed at a later time to transmit quantum information.

    In this work we describe large-scale quantum network architectures that are based on quantum sneakernet principles. We outline the basic information transfer protocols, what are the requirements of the quantum technology to realise this type of network and how a quantum sneakernet can be used to form a high-bandwidth, low error rate truck system to a quantum internet.



  • 21 Apr 2025

    Yutaka Tabuchi (RIKEN Center for Quantum Computing)

    Superconducting quantum computers in RIKEN

    Superconducting quantum computers have garnered significant attention in recent years. Having their scalability and controllability, they are regarded as one of the most promising physical systems for realizing quantum computation. In this presentation, I will give an overview of the superconducting quantum computers based on the ones developed in RIKEN. Furthermore, I discuss gate schemes and control mechanisms for further improvements.


May 2025

  • 05 May 2025

    Malo Cadoret (ONERA, The French Aerospace Lab, Centre de Palaiseau):

    Progress towards the development of a compact quantum cold-atom inertial measurement unit for onboard applications

    Since the 1990’s, a new generation of inertial sensor based on matter-wave interferometry has appeared: accelerometers [1], gradiometers [2] and gyroscopes [3] have been developed and demonstrated high sensitivity, accuracy and long-term stability that outperforms the classical sensors. Major applications for atom interferometers are today geophysics, inertial navigation and fundamental physics. However, most of the quantum sensors are nowadays lab-based experiments and cannot perform onboard measurements, except for some notable exceptions such as ONERA’s marine and airborne gravimeter [4, 5]. In this talk, I will present our progress towards the development of a complete cold-atom Inertial Measurement Unit (IMU). Our goal is to have a single atomic sensor that will alternatively measure each inertial component (3 accelerations and 3 rotations). Every atomic measurement will be hybridized with a set of classical inertial sensors. Hybridization enables to combine the advantages of both classical and quantum technologies and to provide accurate continuous measurements with high dynamic range, in the scope of onboard inertial navigation compatibility. I will present our last results published in [6] regarding the development of a compact atomic gyroscope using magnetically-launched atoms.

    [1] V. Menoret et al., Sci Rep 8, 12300 (2018).
    [2] M. J. Snadden et al. Phys. Rev. Lett 81, 971 (1998)
    [3] T.L. Gustavson et al., Phys. Rev. Lett 78 2046 (1997)
    [4] Y. Bidel et al., Nat. Com. 9 627 (2018)
    [5] Y. Bidel et al., J. Geod. 94 20 (2020)
    [6] C. Salducci et al. Sci. Adv.10,eadq4498 (2024)


  • 12 May 2025

    Rishikesh Gajjala (NYUAD, CQTS):

    Designing Quantum Experiments via Graph Theory

    slides: pdf

    Greenberger–Horne–Zeilinger (GHZ) states are quantum states involving at least three entangled particles. They are foundational in quantum information theory, with practical applications in quantum communication and cryptography. Krenn, Gu, and Zeilinger discovered a correspondence between a class of quantum‐optical experiments that produce GHZ states and edge‐weighted, edge‐coloured multigraphs called GHZ graphs. A graph parameter called dimension can be defined on such a graph, which equals the dimension of the GHZ state generated by the corresponding experiment. Constructing a GHZ graph with a large number of vertices and high dimension would be a major breakthrough, while proving the non‐existence of such graphs (and hence the experiments) has deep implications for quantum resource theory.

    In this talk, I will present our results on this graph‐theoretic question and how they translate to quantum experiments. When there is no destructive interference, these experiments correspond to the special case of unweighted graphs. We provide a complete structural characterization of unweighted GHZ graphs for each dimension. In the more general (edge‐weighted) case, Cervera‑Lierta, Krenn, and Aspuru‑Guzik conjectured that the maximum dimension of an nn-vertex GHZ graph is less than n/2n/2. They verified this via SAT solvers for graphs with up to eight vertices, but nothing was known for larger values of n. We introduce a technique called local sparsification of GHZ graphs, with which we give the first analytical upper bound of n/1.41n/1.41 on the dimension for simple GHZ graphs. Krenn and Gu made a stronger conjecture: that the dimension of any GHZ graph with more than four vertices is at most two (i.e., destructive interference does not help). We show that this holds for infinitely many graphs. Namely, graphs of vertex‐connectivity at most two and for all cubic graphs. Moreover, we prove that any minimal counterexample must be 4‑vertex‑connected. These structural insights both deepen our theoretical understanding and guide automated GHZ‐graph searches (e.g., via PyTheus).



Geometry, Topology & Physics (GTP) Seminar

Weekly seminar, broadly on topics in geometry, (algebraic) topology and theoretical/mathematical physics, with focus on applicability to high energy physics/string theory and quantum systems.


Feb 2022


  • 02 Feb 2022

    Luigi Alfonsi (University of Hertfordshire)

    Higher quantum geometry and global string duality

    video: rec

    In this talk I will discuss the relation between higher geometric quantisation and the global geometry underlying string dualities. Higher geometric quantisation is a promising framework that makes quantisation of classical field theories achievable. This can be obtained by quantising either an ordinary prequantum bundle on the ∞-stack of solutions of the equations of motion or a categorified prequantum bundle on a generalised phase space. I will discuss how the higher quantum geometry of string theory underlies the global geometry of T-duality. In particular, I will illustrate how a globally well-defined moduli stack of tensor hierarchies can be constructed and why this is related to a higher gauge theory with the string 2-group. Finally, I will interpret the formalism of Extended Field Theory as an atlas description of the higher quantum geometry of string theory.



Mar 2022


  • 08 March 2022

    David White (Denison University, USA):

    The Kervaire Invariant, multiplicative norms, and N-infinity operads

    video: rec

    In a 2016 Annals paper, Hill, Hopkins, and Ravenel solved the Kervaire Invariant One Problem using tools from equivariant stable homotopy theory. This problem goes back over 60 years, to the days of Milnorand the discovery of exotic smooth structures on spheres. Of particular importance it its solution were equivariant commutative ring spectra and their multiplicative norms. A more thorough investigation of multiplicative norms, using the language of operads, was recently conducted by Blumberg and Hill, though the existence in general of their new “N-infinity” operads was left as a conjecture. In this talk, I will provide an overview of the Kervaire problem and its solution, I will explain where the operads enter the story, and I will prove the Blumberg-Hill conjecture using a new model structure on the categoryof equivariant operads.


  • 16 March 2022

    Guo Chuan Thiang (Beijing University)

    How open space index theory appears in physics

    video: rec

    The incredible stability of quantum Hall systems and topological phases indicates protection by an underlying index theorem. In contrast to Atiyah-Singer theory for compactified problems, what is required is an index theory on noncompact Riemannian manifolds, with interplay between discrete and continuous spectra. Input data comes not from a topological category a la TQFT, but a metrically-coarsened one. This is the subject of coarse geometry and index theory, and I will explain their experimental manifestations.



Apr 2022



  • 13 April 2022

    Mario Velásquez (Universidad Nacional de Colombia)

    The Baum-Connes conjecture for groups and groupoids

    In this talk we present some basics definitions around the Baum-Connes conjecture in the context of groups and groupoids, in particular we define the reduced C *C^\ast-algebra C r *(G)C_r^*(G) of a groupoid G. When a group (or groupoid) satisfies this conjecture we present how we can compute the topological K-theory of C r *(G)C_r^*(G) via a classifying space. We also present some explicit computations and an application about Fredholm boundary conditions in manifolds with corners.


  • 27 April 2022

    Amnon Neeman (Australian National University)

    Bounded t-structures and stability conditions

    We will give a gentle introduction to the topic. We will review the definitions of derived and triangulated categories, of t-structures an of stability conditions. The only new result will come at the very end of the talk, a theorem saying that there are no stability condition on the derived category of bounded complexes of vector bundles on a singular scheme.


May 2022


  • 11 May 2022

    Alex Fok (NYU Shanghai)

    Equivariant twisted KK-theory of noncompact Lie groups

    The Freed-Hopkins-Teleman theorem asserts a canonical link between the equivariant twisted K-theory of a compact Lie group equipped with the conjugation action by itself and the representation theory of its loop group. Motivated by this, we will present results on the equivariant twisted KK-theory of a noncompact semisimple Lie group GG. We will give a geometric description of generators of the equivariant twisted KK-theory of G with equivariant correspondences, which are applied to formulate the geometric quantization of quasi-Hamiltonian manifolds with proper G-actions. We will also show that the Baum-Connes assembly map for the C *C^\ast-algebra of sections of the Dixmier-Douady bundle which realizes the twist is an isomorphism, and discuss a conjecture on representations of the loop group LGL G. This talk is based on joint work with Mathai Varghese.


Sep 2022




Oct 2022

The infinity topos of differentiable sheaves contains all smooth manifolds as a full subcategory and has excellent formal properties. In particular, it admits an intrinsic notion of underlying homotopy type of any differentiable sheaf, which coincides with classical constructions such as taking smooth total singular complexes. Moreover, there is a canonical sense in which the mapping sheaf between any two differentiable sheaves may have the correct homotopy type. This latter notion is reminiscent of the Oka principle in complex geometry. In this talk I will show how to exhibit the Oka principle in the smooth setting using model structures and other homotopical calculi on the infinity topos of differentiable sheaves.




Nov 2022


  • 23 Nov 2022

    Valentino Foit (NYUAD)

    Brownian loops and conformally invariant systems

    slides: pdf

    video: rec, YT

    The Brownian loop soup (BLS) is a stochastic system that is constructed from random loops in the plane and is invariant under conformal transformations. Correlation functions of certain observables can be used to formulate the BLS as a Conformal Field Theory (CFT). I will give an overview of CFTs in two dimensions and point out their relation to certain stochastic systems. Then I will discuss the BLS including some recent progress, such as the operator content, the continuous spectrum, and hints of an extended symmetry algebra.


  • 30 Nov 2022

    Allan Merino,

    Classification and double commutant property for dual pairs in an orthosymplectic Lie supergroup

    video: rec

    One of the main problems in representation theory is to determine the set of equivalence classes of irreducible unitary representations of a Lie group. Using the Weil representation, Roger Howe established a one-to-one correspondence (known as the local theta correspondence) between particular representations of two subgroups GG and G′G' forming a dual pair in Sp(W)Sp(W). This correspondence provides a nice way to construct unitary representations of small Gelfand-Kirillov dimension.

    In his wonderful paper “Remarks on classical invariant theory”, Roger Howe suggested that his classical duality should be extendable to superalgebras/supergroups. In a recent work with Hadi Salmasian, we obtained a classification of irreducible reductive dual pairs in a real or complex orthosymplectic Lie supergroup SpO(V)SpO(V). Moreover, we proved a “double commutant theorem” for all dual pairs in a real or complex orthosymplectic Lie supergroup.

    In my talk, I will spend quite some time explaining how the Howe duality works in the symplectic case and then talk about the results we obtained in our paper with H. Salmasian. [arXiv:2208.09746]


Dec 2022

  • 07 Dec 2022

    Emily Riehl (Johns Hopkins University)

    ∞\infty-Category theory for undergraduates

    video: rec, YT

    cf.: arXiv:2302.07855, AMS Notices

    At its current state of the art, ∞ \infty -category theory is challenging to explain even to specialists in closely related mathematical areas. Nevertheless, historical experience suggests that in, say, a century’s time, we will routinely teach this material to undergraduates. This talk describes one dream about how this might come about — under the assumption that 22nd century undergraduates have absorbed the background intuitions of homotopy type theory/univalent foundations.



Jan 2023



Feb 2023



  • 22 Feb 2023

    Dmitry Kozlov

    Applied and Computational Topology

    video: YT

    We will give a brief introduction to the subject of Applied and Computational Topology. The survey of the subject’s main ideas and tools will be complemented with applications to discrete mathematics and to theoretical distributed computing. We will conclude with stating an open problem in combinatorial topology which is related to the complexity of the Weak Symmetry Breaking distributed task.


Mar 2023




Apr 2023





May 2023



Sep 2023




Oct 2023


  • 11 Oct 2023

    Cihan Okay (Bikent University):

    Simplicial Distributions and Contextuality

    video: YT, Zm

    cf. arXiv:2204.06648

    In modern homotopy theory, spaces are represented by combinatorial models called simplicial sets. Their elegant formulation gives them great expressive power to capture spaces up to homotopy. Simplicial distributions are basic mathematical objects that mix simplicial sets with probabilities. That is, they model probability distributions on spaces. In my talk, I will show how simplicial distributions provide a framework for studying a central quantum feature associated with probabilities, known as contextuality. A typical measurement scenario consists of a set of measurements and outcomes, whereas simplicial distributions can be defined for spaces of measurements and outcomes. Our approach unifies and goes beyond two earlier approaches: the sheaf-theoretic (Abramsky-Brandenburger) and group cohomological (Okay-Roberts-Bartlett-Raussendorf).




Nov 2023





Dec 2023



Jan 2024

  • 24 Jan 2024:

    Quentin Ehret:

    Central extensions of restricted Lie superalgebras and classification of pp-nilpotent Lie superalgebras in dimension 4

    video: kt

    cf.: arXiv:2401.08313

    Over a field of positive characteristic pp, restricted Lie algebras are of prime interest, mainly due to their link to algebraic groups and their role in representation theory and classification. The cohomology associated with restricted Lie algebras is considerably more complicated than the ordinary Chevalley-Eilenberg cohomology and explicit formulas are only known up to order 2. In this talk, I will explain how to build the first and second restricted cohomology groups for restricted Lie superalgebras in characteristic pp greater than 3, modifying a previous construction. I will explain how these groups capture some algebraic structures, such as restricted extensions. Further, I will show how to apply this construction to classify pp-nilpotent restricted Lie superalgebras up to dimension 4 over an algebraically closed field of characteristic pp greater than 3. This is a joint work with Sofiane Bouarroudj (NYU Abu Dhabi).


  • 31 Jan 2024

    Chris Blair:

    Geometry and Dualities of Decoupling Limits in String Theory and M-Theory

    cf.: arXiv:2311.10564

    video: zm, kt

    Our understanding of M-theory is based on a duality web connecting different limits of the theory. I’ll discuss the extension of this duality web to a wide variety of decoupling limits related by duality to the null reduction of M-theory (and hence to the proposal that M-theory can be described by Matrix theory). From a modern perspective, these limits involve non-relativistic geometries, leading to new variants of supergravity in 11- and 10-dimensions. I’ll discuss how to systematically explore these corners of M-theory, following the roadmap of arxiv.org/abs/2311.10564.


Feb 2024


  • 14 Feb 2024

    Babak Haghighat (Tsinghua University, China):

    Flat Connections from Irregular Conformal Blocks

    cf. arXiv:2311.13358, arXiv:2311.07960

    video: zm, kt

    I will talk about Liouville conformal blocks with degenerate primaries and one operator in an irregular representation of the Virasoro algebra. Using an algebraic approach, we derive modified BPZ equations satisfied by such blocks and subsequently construct corresponding integral representations based on integration over non-compact Lefschetz cycles. The integral representations are then used to derive novel types of flat connections on the irregular conformal block bundle.


Mar 2024

  • 06 Mar 2024

    Du Pei (Centre for Quantum Mathematics, University of Southern Denmark):

    On New Invariants and Phases of Supersymmetric Quantum Field Theories

    video: Zm, kt

    In this talk, we will explore a novel approach to study supersymmetric quantum field theories using tools from stable homotopy theory. We will explain how this approach leads to new invariants that can be used to detect subtle differences between phases that escape the detection of more conventional invariants.



Apr 2024

  • Alexander Stottmeister (Leibniz Universität Hannover):

    Embezzlement of entanglement and the classification of von Neumann algebras

    cf.: arXiv:2401.07299

    We discuss the embezzlement of entanglement in the setting of von Neumann algebras and its relation to the classification of the latter. Embezzlement (of entanglement), introduced by van Dam and Hayden, denotes the task of producing any entangled state to arbitrary precision from a shared entangled resource state, the embezzling state, using local operations without communication while perturbing the resource arbitrarily little.

    We show that Connes’ classification of type III von Neumann algebras can be given a quantitative operational interpretation in terms of embezzlement. This quantification implies that all type III factors, apart from some type III 0III_0 factors, host embezzling states. In contrast, semifinite factors (type I or II) cannot host embezzling


May 2024



  • 13 May 2024

    Iman Marivan (Duke University):

    Locality, Symmetry, and Coherence Through the Lens of Quantum Information

    The primary goal of quantum information science is to harness the power of quantum systems for computing and information-processing tasks. Interestingly, the quantum information perspective also provides new insights and raises new questions about the fundamental concepts of locality, symmetry, and coherence. In the first part of my talk, I will discuss an ongoing project focused on understanding the implications of symmetries and the locality of interactions within the framework of quantum circuits.


Sep 2024

  • 04 Sep 2024

    Alessandro Portaluri (University of Torino and NYUAD):

    Index and Stability of (Semi-)Riemannian Closed Geodesics

    cf. arXiv:1907.05864

    A celebrated result proved by Poincaré affirms that a closed non-degenerate minimizing geodesic on an oriented surface is hyperbolic. Starting from this classical theorem and by using some recent results on the Maslov index and on the Spectral Flow, we will present a general instability criterion for timelike and spacelike closed (semi-)Riemannian geodesics on (non-)oriented manifolds of any dimension.



  • 18 Sep 2024

    Mitchell Riley (CQTS @ NYUAD):

    Lazy Algorithms in Algebraic Topology

    cf. github.com/mvr/at

    Finite simplicial complexes are easily represented on a computer as lists of the simplices that they contain. In this form, it is not difficult to perform constructions involving them or compute invariants such as their homology. However, most spaces important to algebraic topology cannot be represented in this way, and so a new strategy is needed.

    Effective Algebraic Topology is a collection of techniques for manipulating certain infinite simplicial sets algorithmically, retaining the ability to perform the same sorts of calculations as in the finite case. I will give an overview of the field and demonstrate some of the computations that can be performed.


Oct 2024

  • 09 Oct 2024

    Nikita Golub (Saint Petersburg State University):

    Functorial Languages in Homological Algebra

    slides: pdf

    cf.: arXiv:2410.05708

    In our talk, we shall dive into a number of phenomena related to the higher limit approach to the description of functors of homological nature. The first examples appeared in the work of Quillen on Hochschild homology of algebras, where he showed that Hochschild homology of an algebra can be represented as limits of some functors from the category of free extensions of a given algebra. Further similar formulas were derived by Roman Mikhailov and Sergey Ivanov in the context of group homology, who showed that group homology of a group can be expressed as higher limits of certain functors along the category of free extensions of the group. They further proposed the construction of fr-language, where f\mathbf{f} and r\mathbf{r} are some functorial ideals of the functor of group rings. It allows us to describe lots of graded functors from the category of groups to the category of abelian groups by simple expressions of the form fr+rf\mathbf{f}\mathbf{r} + \mathbf{r}\mathbf{f}, rr+frf\mathbf{r}\mathbf{r} + \mathbf{f}\mathbf{r}\mathbf{f}.

    In our work, we have provided a formalisation of their construction and constructed new languages using the lower central series, which have a close connection with nilpotency. We notice that these functorial languages acquire remarkable properties when we restrict them to different varieties of groups.

    We will lift all constructions to spectra and demonstrate that functorial languages on a given manifold of groups (or simply subcategories of a category of groups) give rise to some stable infinity-categories, which we call functorial surfaces. Then applying the algebraic K-theory to functorial surfaces, we arrive at flux spectra. This may provide a bridge between group theory and stable homotopy theory.


  • 23 Oct 2024

    Nizar Demni (Aix-Marseille Université (AMU) France and NYUAD):

    From the Dunkl Intertwining Operator to Simple Hurwitz Numbers

    slides: pdf

    I’ll start with a review of finite root systems and their related matters (Weyl chambers, reflection groups, multiplicity functions). Then, I’ll introduce the Dunkl derivatives and the Dunkl intertwining operator. In this context, I’ll discuss the commutativity of the former and the existence of the latter, relying on a deformed de Rham cohomology and the reflection group algebra. Finally, I’ll focus on the Itzykson-Zuber-Harish-Chandra integral, its various expansions, and raise the problem of a mysterious connection to simple Hurwitz numbers.


Nov 2024



Dec 2024

  • 04 Dec 2024

    Lukas Woike (Bourgogne University, France):

    Skein Algebras and Skein Modules Beyond Semisimplicity

    slides: pdf

    cf. arXiv:2409.17047, arXiv:2212.11259

    Skein-theoretic methods play an important role for the construction of topological field theories and related structures. Classically, these methods use ribbon fusion categories as an input and hence need semisimplicity. In this talk, I will discuss generalizations of skein theory that work beyond semisimplicity, and partly even without rigid duals. To this end, I will give an overview of different joint papers with Brochier and Müller and explain the relation to work of Costantino-Geer-Patureau-Mirand, Brown-Haïoun and Runkel-Schweigert-Tham on admissible skeins.


  • 11 Dec 2024

    Simone Noja (Heidelberg University, Germany):

    The Geometry of Pure Spinor Superfield Formalism

    slides: pdf

    cf.: arXiv:2404.07167

    In this talk I will introduce a mathematical perspective on the pure spinor superfield formalism. In particular, I will discuss how multiplets of fields appearing in supersymmetric theories can be constructed mathematically from geometric data related to certain algebraic varieties – the nilpotence variety of the (super)symmetry algebra of the theory. After discussing some relevant examples, if time permits, I will hint at a generalization of the formalism in the direction of derived geometry.


Feb 2025




Mar 2025

  • 5 Mar 2025

    Leonardo Santilli (Tsinghua University, China):

    Defects, SymTFTs, and (−1)(-1)-form symmetry from M-theory

    slides: pdf

    cf.: arXiv:2411.19683

    I will highlight some tensions in the treatment of higher form symmetries, when the theory possesses a (d−1)(d-1)-form symmetry. I will then show how, for invertible symmetries, the tensions are automatically resolved dealing with (−1)(-1)-form symmetries in the formalism of gerbes. After this general introduction and motivation, I will review the geometric engineering of defects in M-theory. I will then proceed to obtain the SymTFT of M-theory compactifications, using differential cohomology as the main tool. In this way, I will provide a comprehensive treatment of defects and symmetries via geometric engineering, and derive the (−1)(-1)-form symmetries and their anomalies from this perspective. I will conclude with explicit examples and dynamical applications.




Apr 2025




May 2025



External presentations

The following is a (very) inclomplete list of selected invited presentations by CQTS members at other institutes.


Sep 2022


  • 16 Sep 2022 at Math Faculty Meeting, NYU Abu Dhabi

    Urs Schreiber on joint work with Hisham Sati:

    Practical Foundations for Topological Quantum Programming

    slides: pdf


Nov 2022


Dec 2022


Jan 2023




Feb 2023



Mar 2023

Asif Equbal (far left) and Amaria Javed (far right)


Apr 2023

  • 10 Apr 2023

    David Jaz Myers:

    How do you identify one thing with another? – an intro to Homotopy Type Theory

    talk at Prof. Sadok Kallel‘s colloquium,

    American University of Sharjah

    slides: pdf



Aug 2023


Feb 2024




Jul 2024


Sep 2024



Feb 2025









category: reference

Last revised on June 2, 2025 at 20:32:22. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (462 revisions) Cite Print Source