nLab topological data analysis
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Constructivism, Realizability, Computability
constructive mathematics, realizability, computability
propositions as types, proofs as programs, computational trinitarianism
Constructive mathematics
Realizability
Computability
Topological data analysis
Idea
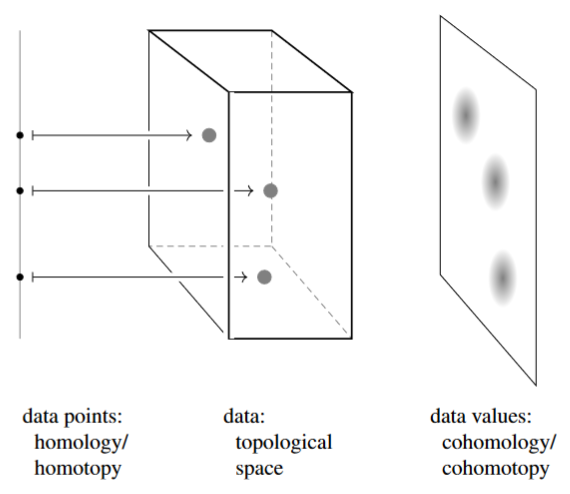
Topological data analysis (TDA) is qualitative data analysis with tools from topology, in particular with tools from algebraic topology, aiming to extract (hidden) structure in large datasets which is robust against uncertainties and noise.
This notably includes tools from ordinary (co-)homology-theory, which in the guise of persistent homology has become the signature method in TDA; but it also includes more general tools of homotopy theory and differential topology, which have more recently found their way into TDA in the guise of persistent homotopy theory and persistent cohomotopy theory. (graphics from SS22)
Typically, TDA deals with large data sets modeled as (subsets of) topological spaces. Collections of data points appear as cycles in the topological space of data, and values of data appear as cocycles.
Strategy of persistent topology/homotopy
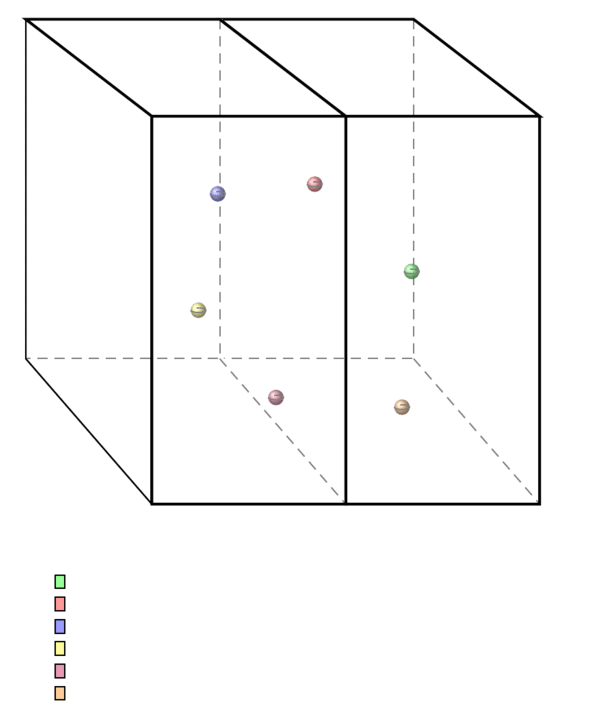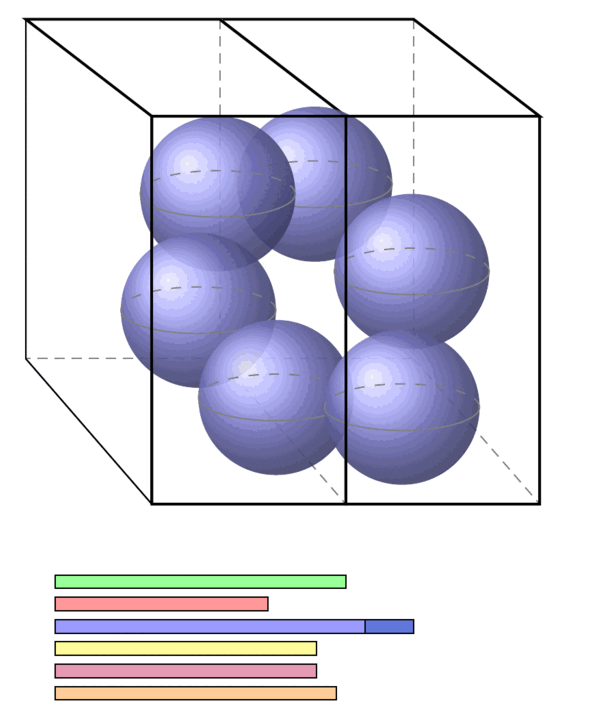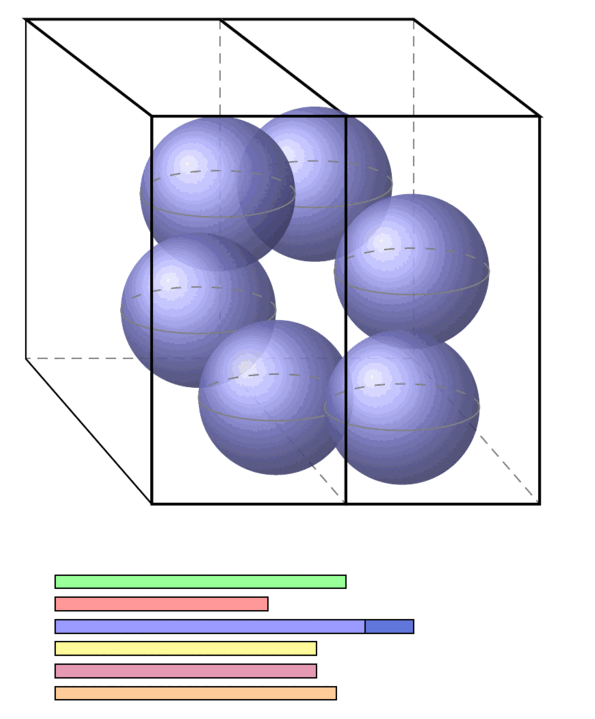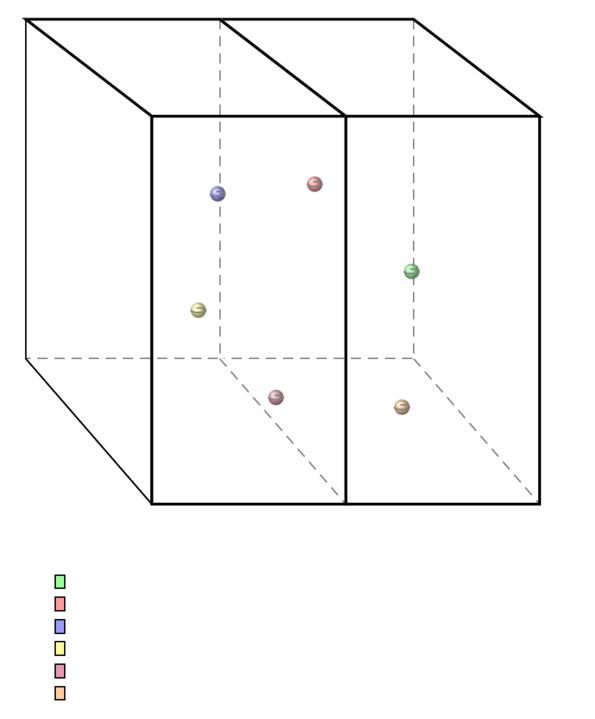
The strategy of persistent homology/homotopy in TDA is to see which chunks (subspaces) of the data appear to be (higher) connected when viewed at some resolution (technically: at some filter stage) and how much these apparent chunks persist as the resolution changes. This may be recorded in persistence diagrams also known as “barcodes”.
The fundamental theorem of the field – the stability theorem – says that persistent (co-)cycle-classes are indeed a good invariant of data, in that they remain stable under small perturbations of the initial data (e.g. under noise, uncertainty, measurement errors, etc.).
The idea then is that those (co-)cycles which persist for longer (appear as longer bars in the barcode) reflect relevant structure hidden in the (large) data set.
However, it is often unclear (and certainly not part of the mathematical theory) what significance or meaning any persistent cycle has for the practical problem of interpreting data. (graphics from SS22)
Strategy of persistent cohomology/cohomotopy
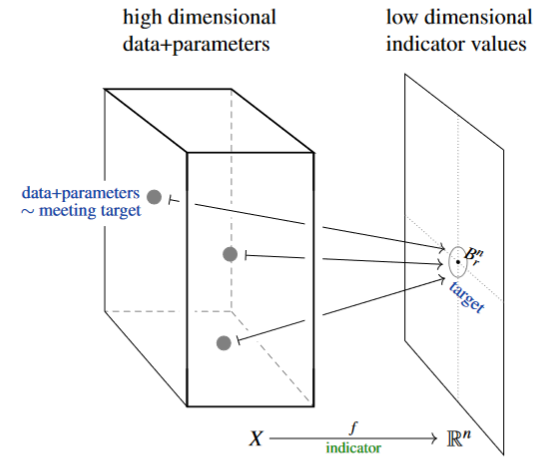
In contrast, persistent cohomotopy in TDA is the effective answer to a concrete and common question in data analysis:
Given a large-dimensional space of data, and a small number of (real) indicator values assigned to each data point with given precision , does any data meet a prescribed target indication precisely?
A fundamental theorem of persistent Cohomotopy (Franek, Krčál & Wagner 2018, Franek & Krčál 2017, p. 5, see here) shows that (1.) the answer to this question is detected by a certain Cohomotopy-class and (2.) in a fair range of dimensions, this Cohomotopy class is provably computable, hence the above question is effectively decidable. (graphics from SS22)
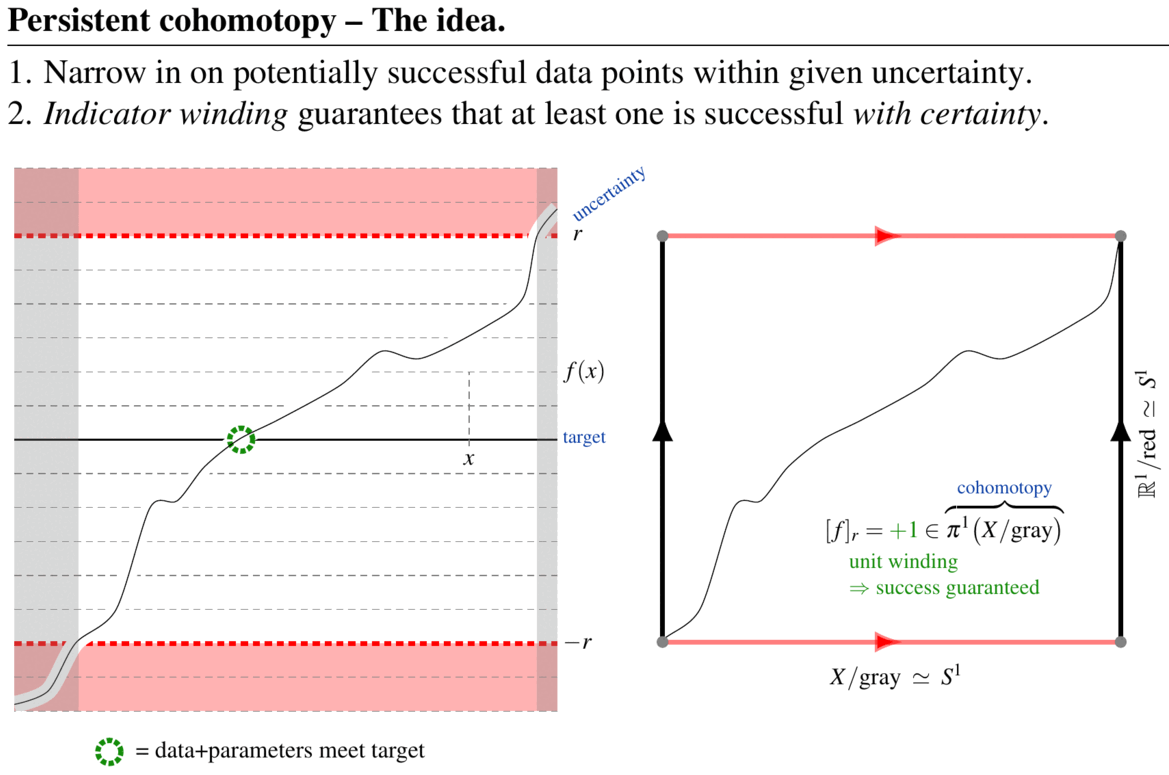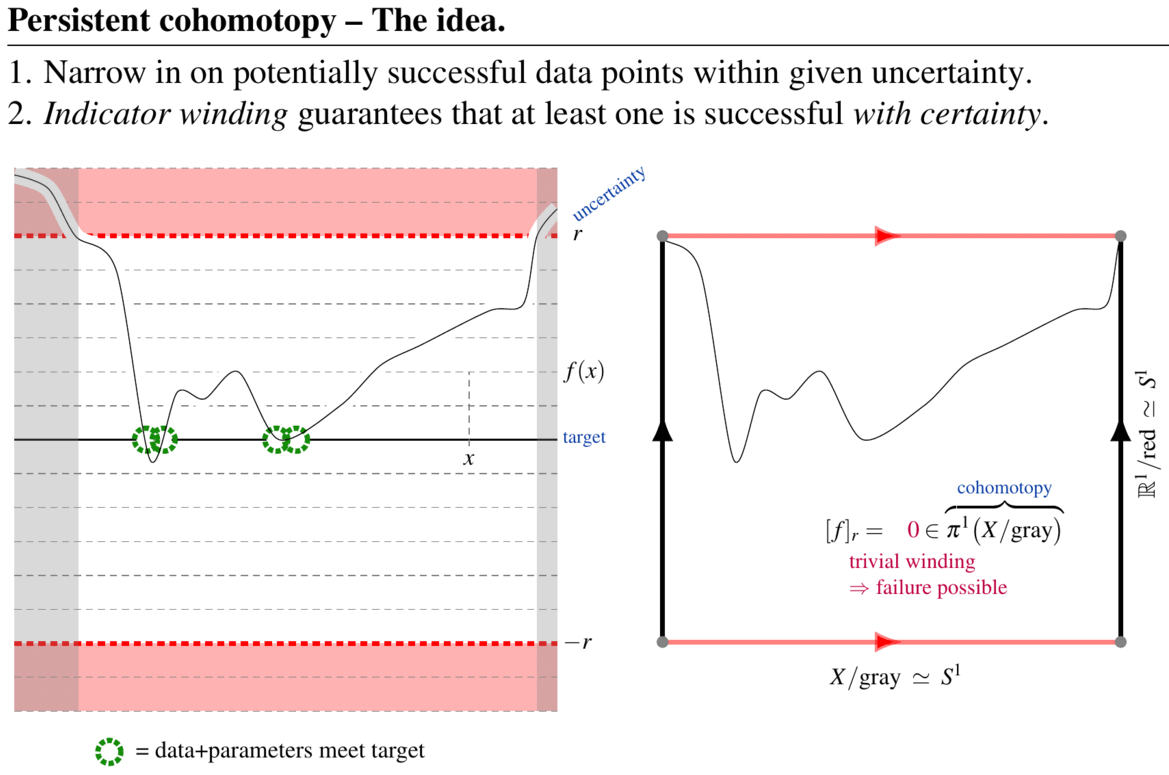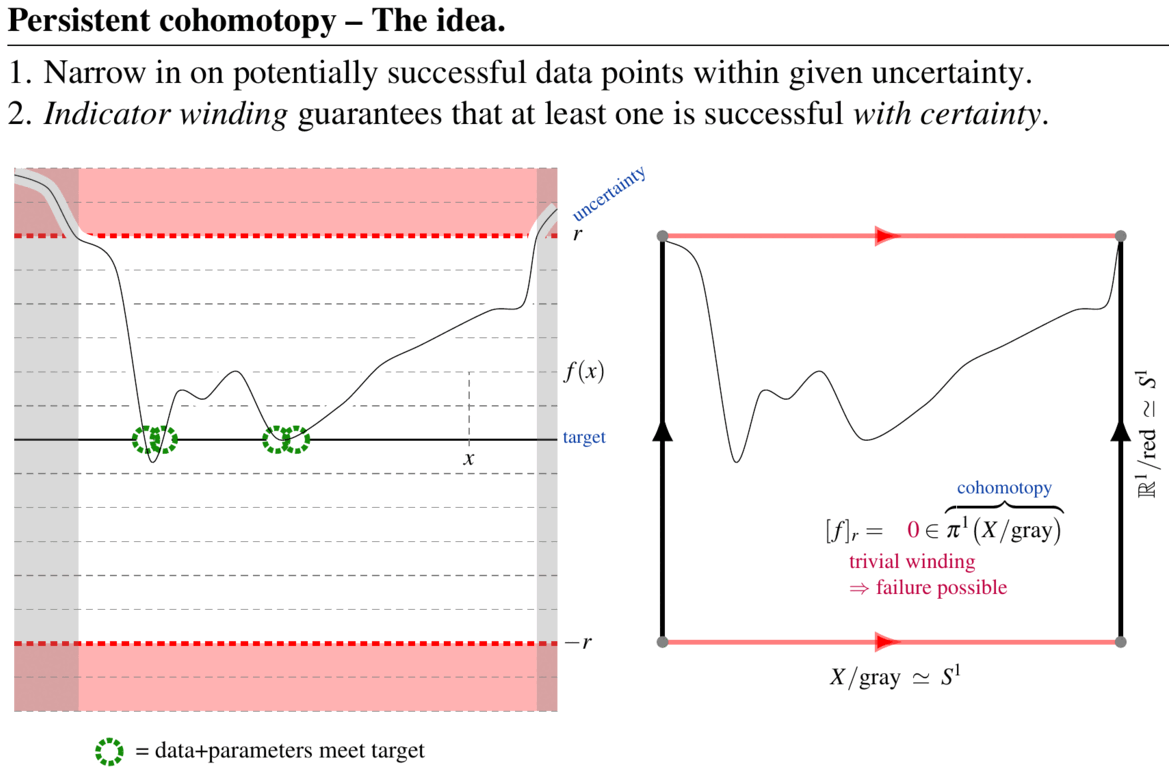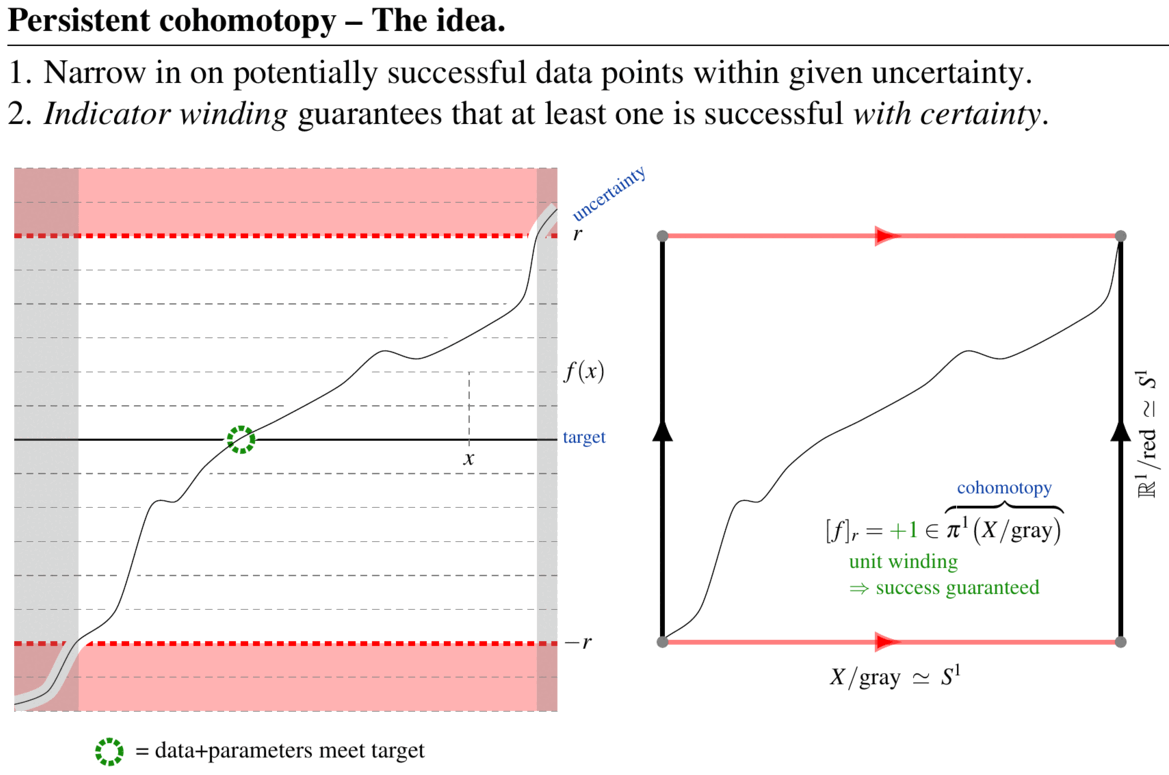
(graphics from SS22)
(Alternatively, with tools from persistent homology theory an answer to this question is given by the method of well groups – but (1.) it is known that well groups are in general too coarse to provide a complete answer and (2.) despite effort it remains unknown if well groups are actually computable in relevant cases, see Franek & Krčál 2016.)
If the topological space of data may be assumed to be a smooth manifold (indeed, in typical examples is itself a large-dimensional Cartesian space) then persistent cohomotopy may be understood dually via Pontryagin's theorem as characterizing iso-hypersurfaces of data (close to a given target indicator) by framed cobordism theory (Franek & Krčál 2017, p. 8-9). The full implications of this relation for topological data analysis remain to be explored.
Related concepts
References
General
General introduction and survey:
-
Robert Ghrist, Barcodes: The Persistent Topology of Data, Bull. Amer. Math. Soc. 45 (2008), 61-75 (doi:10.1090/S0273-0979-07-01191-3, pdf)
-
Herbert Edelsbrunner, John Harer, Persistent homology – a survey, in: Surveys on Discrete and Computational Geometry: Twenty Years Later, Contemporary Mathematics 453 (2008) doi:10.1090/conm/453
-
Gunnar Carlsson, Topology and data, Bull. Amer. Math. Soc. 46 (2009), no. 2, 255-308 doi:10.1090/S0273-0979-09-01249-X
-
Herbert Edelsbrunner, Dmitriy Morozov, Persistent homology: theory and practice, in: European Congress of Mathematics Kraków, 2–7 July, 2012 EMS doi:10.4171/120-1/3, pdf
-
Steve Y. Oudot, Persistence Theory: From Quiver Representations to Data Analysis, Mathematical Surveys and Monographs 209 AMS (2015) pdf, ISBN:978-1-4704-3443-4
-
Gunnar Carlsson, Persistent Homology and Applied Homotopy Theory, in: Handbook of Homotopy Theory, CRC Press (2019) arXiv:2004.00738, doi:10.1201/9781351251624
-
Donald Pinckney, Topological Data Analysis and Persistent Homology (2019)
Flashy exposition for commercial use:
- Gunnar Carlsson, Professor Gunnar Carlsson Introduces Topological Data Analysis video
See also:
- Wikipedia, Topological data analysis
and see the references at
Implementation
Implementation via concrete algorithms, etc.
- Gurjeet Singh, Facundo Mémoli, Gunnar Carlsson, Topological Methods for the Analysis of High Dimensional Data Sets and 3D Object Recognition, in: M. Botsch, R. Pajarola (eds.), Eurographics Symposium on Point-Based Graphics (2007) doi:10.2312/SPBG/SPBG07/091-100, pdf
Review:
- Stefan Huber, Persistent Homology in Data Science In: Data Science – Analytics and Applications Springer (2021) doi:10.1007/978-3-658-32182-6_13, pdf
Applications
Application of topological data analysis (persistent homology) to
analysis of quasicrystals:
- Pavlo Solokha et al., New Quasicrystal Approximant in the Sc–Pd System: From Topological Data Mining to the Bench, Chem. Mater. 2020, 32, 3, 1064–1079 (doi:10.1021/acs.chemmater.9b03767)
analysis of cosmological structure formation:
- Matteo Biagetti, Alex Cole, Gary Shiu, The Persistence of Large Scale Structures I: Primordial non-Gaussianity (arXiv:2009.04819)
analysis of phase transitions:
- Alex Cole, Gregory J. Loges, Gary Shiu, Quantitative and Interpretable Order Parameters for Phase Transitions from Persistent Homology (arXiv:2009.14231)
recognition of instantons and confinement in lattice gauge theory:
- Daniel Spitz, Julian M. Urban, Jan M. Pawlowski, Confinement in non-Abelian lattice gauge theory via persistent homology [arXiv:2208.03955]
analysis of the cosmic microwave background in search for hints of inhomogeneous cosmology:
- Pratyush Pranav, Thomas Buchert, Homology reveals significant anisotropy in the cosmic microwave background [arXiv:2308.10738]
Persistent homology has strong computational limits for large data sets and major problems with multifitrations. An alternative propoposal in TDA to persistent homology which is worse in 1 dimension but does not suffer above problems is
- Paweł Dłotko, Davide Gurnari, Euler Characteristic Curves and Profiles: a stable shape invariant for big data problems, arXiv:2212.01666
Relation to quantum computation
Potential implementation of TDA on quantum computers:
-
Seth Lloyd, Silvano Garnerone, Paolo Zanardi, Quantum algorithms for topological and geometric analysis of big data, Nat Commun 7 10138 (2016) [arXiv:1408.3106, doi:10.1038/ncomms10138]
-
He-Liang Huang, Xi-Lin Wang, Peter P. Rohde, Yi-Han Luo, You-Wei Zhao, Chang Liu, Li Li, Nai-Le Liu, Chao-Yang Lu, Jian-Wei Pan, Demonstration of Topological Data Analysis on a Quantum Processor, Optica 5(2), 193 (2018) (arXiv:1801.06316)
-
Massimiliano Incudini, Francesco Martini, Alessandra Di Pierro, Higher-order topological kernels via quantum computation, 2023 IEEE International Conference on Quantum Computing and Engineering, QCE 1 (2023) [arXiv:2307.07383, doi:10.1109/QCE57702.2023.00076]
See also:
-
Roberto Zucchini, A new quantum computational set-up for algebraic topology via simplicial sets, Journal of AppliedMath 3 4 (2025) [doi:10.59400/jam3011, arXiv:2309.11304, spire:2700409]
-
Roberto Zucchini, A New Quantum Computational Setup for Algebraic Topology via Simplicial Sets, talk at CQTS (May 2024) [pdf]
Cohomotopy in topological data analysis
Introducing persistent cohomotopy as a tool in topological data analysis, improving on the use of well groups from persistent homology:
-
Peter Franek, Marek Krčál, On Computability and Triviality of Well Groups, Discrete Comput Geom 56 (2016) 126 (arXiv:1501.03641, doi:10.1007/s00454-016-9794-2)
-
Peter Franek, Marek Krčál, Persistence of Zero Sets, Homology, Homotopy and Applications, 19 2 (2017) (arXiv:1507.04310, doi:10.4310/HHA.2017.v19.n2.a16)
-
Peter Franek, Marek Krčál, Hubert Wagner, Solving equations and optimization problems with uncertainty, J Appl. and Comput. Topology 1 (2018) 297 (arxiv:1607.06344, doi:10.1007/s41468-017-0009-6)
Review:
-
Peter Franek, Marek Krčál, Cohomotopy groups capture robust Properties of Zero Sets via Homotopy Theory, talk at ACAT meeting 2015 pdf
-
Urs Schreiber on joint work with Hisham Sati: New Foundations for TDA – Cohomotopy, (May 2022)
Last revised on August 18, 2025 at 18:35:21. See the history of this page for a list of all contributions to it.