Schreiber The Character Map in Equivariant Twistorial Cohomotopy

An article that we are finalizing at CQTS:

---

• Hisham Sati$\;$ and $\;$ Urs Schreiber:

  
  

  The character map in Equivariant Twistorial Cohomotopy

  
  

  to appear in:

  
  

  Applied Algebraic Topology

  special issue of

  Beijing Journal of Pure and Applied Mathematics

  (March 2025)

  
  

  download:

  • pdf (v2: intro and outlook rewritten, aimed at applied algebraic topologist readers)

  • arXiv:2011.06533 (v1)

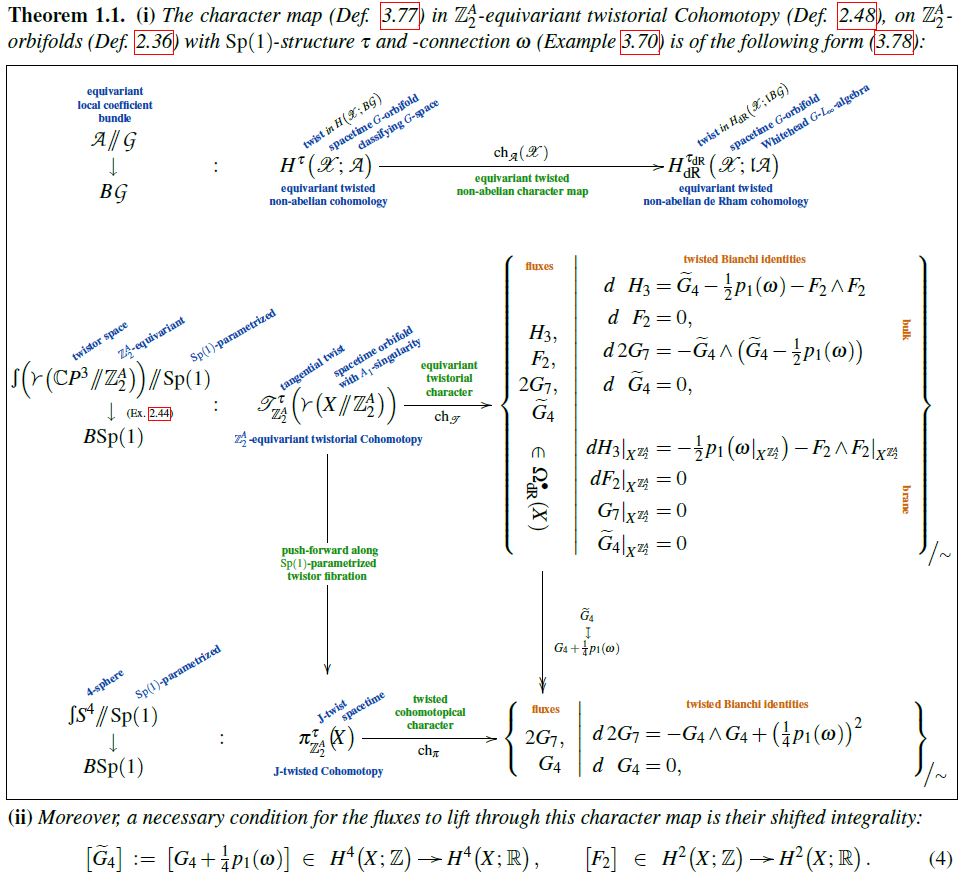
Abstract. The fundamental notion of non-abelian generalized cohomology gained recognition in algebraic topology as the nonabelian Poincaré-dual to “factorization homology”, and in theoretical physics as providing flux-quantization for non-linear Gauß laws. However, already the archetypical example — unstable Cohomotopy, first studied almost a century ago by Pontrjagin — may remain underappreciated as a cohomology theory.

In illustration and amplification of its cohomological nature, we construct the non-abelian generalization of the Chern character map on $\mathbb{Z}/2$-equivariantized 7-Cohomotopy — in fact on its “twistorial” version classified by complex projective 3-space — essentially by computing its equivariant Sullivan model, and we highlight some interesting integral cohomology classes which are extracted this way. We end with an outlook on the application of this result to the the rigorous deduction of the proposed anyonic quantum states on M5-branes wrapped over Seifert 3-orbifolds.

Building on:

• The Character Map in Non-Abelian Cohomology

• Twistorial Cohomotopy implies Green-Schwarz anomaly cancellation

---

---