nLab wrapped brane

Idea

In physics (string theory), a (factor space of a) brane worldvolume $\phi \colon \Sigma \longrightarrow X$ is said to wrap a cycle $c \in H_{\dim(\Sigma)}(X)$ in spacetime $X$ when the pushforward $\phi_\ast [\Sigma] \in H_\bullet(X)$ of the fundamental class of the manifold (or orbifold) $\Sigma$ is the class, $[c]$, of the given cycle in $X$. If the pushforward is a multiple of $[c]$, then the brane is said to wrap $c$ multiple times.

Here $H_\bullet$ is typically taken to be ordinary homology but may also be K-homology (cf. D-brane charge quantization in K-theory) and could in principle by any other generalized homology-theory thought to encode the flux quantization.

In mathematics (algebraic topology), a cycle represented by a manifold this way is said to be Steenrod representable.

Examples

Via the identification of D-brane charge in K-theory, the K-theoretic McKay correspondence formalizes how D-branes wrap the fundamental cycles in the blow-up resultion of an ADE-singularity (Gonzalez-Sprinberg & Verdier 83)

• membrane instanton

• M5-brane instanton

• fractional M2-brane

• 3d-3d correspondence

• giant graviton

• in the Witten-Sakai-Sugimoto model (see there) for non-perturbative quantum chromodynamics baryons appear as wrapped D4-branes

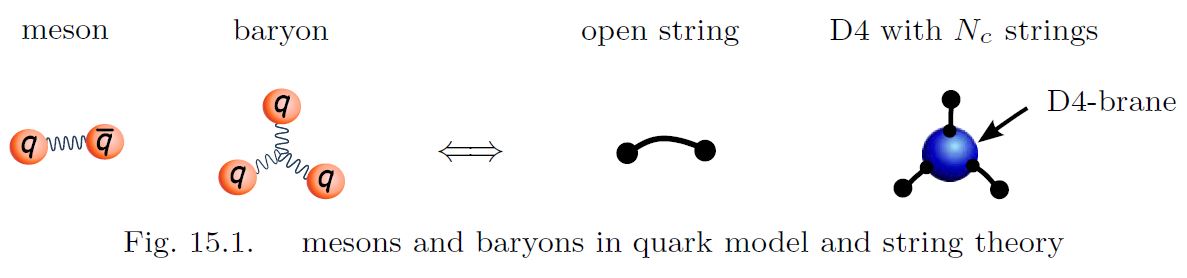
graphics grabbed from Sugimoto 16

Related concepts

• polarized brane

• brane intersection

• Dp-D(p+2)-brane bound state

• Dp-D(p+4)-brane bound state

References

• Gérard Gonzalez-Sprinberg, Jean-Louis Verdier, Construction géométrique de la correspondance de McKay, Ann. Sci. ́École Norm. Sup.16 (1983) 409–449. (numdam)

• Shigeki Sugimoto, Skyrmion and String theory, chapter 15 in Mannque Rho, Ismail Zahed (eds.) The Multifaceted Skyrmion, World Scientific 2016 (doi:10.1142/9710)