nLab Cayley-Dickson construction

Idea

The Cayley-Dickson construction or Cayley-Dickson double (Dickson 1919, (6)) takes a real star-algebra $A$ to a new real star-algebra whose elements are pairs of elements of $A$, in generalization of how the complex numbers arise as a doubling of the real numbers.

When iteratively applied to the real numbers, regarded as a star-algebra with trivial involution, the Cayley-Dickson construction yields, consecutively, the complex numbers, then the quaternions, then the octonions (thus all four real normed division algebras), then the sedenions, …

Definition

Let $A$ be an possibly nonassociative star-algebra over the field $\mathbb{R}$ of real numbers: an algebra equipped with an involution $\overline(-) \colon x \mapsto \overline{x}$ which is an antiautomorphism. (Actually, $\mathbb{R}$ could be replaced by any commutative ring in the definitions, although some properties may depend on this ring.)

Definition in components

Definition

(Cayley-Dickson construction in components)

The Cayley–Dickson double of the real star-algebra $A$ is the real star-algebra $CD(A)$

• whose underlying real vector space is the direct sum $A \oplus A$,

• whose multiplication is given by

  (1)$$(a,b) (c, d) \;\coloneqq\; (a c - d \overline{b}, \overline{a} d + c b)$$

• whose star-involution is given by

  (2)$$\widebar{(a,b)} \;\coloneqq\; (\overline{a},-b) \,.$$

(Dickson 1919, (6))

Definition by generators and relations

Definition

(Cayley-Dickson double by generators and relations)

The Cayley-Dickson double of a real star-algebra $A$ is the real star-algebra $\widetilde{CD}(A)$ obtained by adjoining one generator $\ell$ to $A$ subject to the following relations:

(3)$$\ell^2 \;=\; -1 \,, \phantom{AAA} \overline{\ell} \;=\; - \ell$$

and

(4)$$a (\ell b) = \ell (\overline{a} b) \,, \phantom{AA} (a \ell) b = (a \overline{b}) \ell \,, \phantom{AA} (\ell a) (b \ell) = - \overline{a b}$$

for all $a, b \in A$.

(Baez 02, second half of 2.2)

Lemma

(induced relations)

The relation in Def. imply the following further relations:

(5)$$a \ell \;=\; \ell \overline{a} \,, \phantom{AA} \ell a \;=\; \overline{a} \ell$$

$$(\ell a) b \;=\; \ell (b a) \,, \phantom{AA} a (b \ell) \;=\; (b a) \ell$$

(6)$$(\ell a) (\ell b) \;=\; - b \overline{a} \,, \phantom{AA} (a \ell) (b \ell) \;=\; - \overline{b} a$$

for all $a, b \in A$.

Proof

Using (4) we have:

$$\begin{aligned} a \ell & = a (\ell 1) \\ & = \ell (\overline{a} 1) \\ & = \ell \overline{a} \end{aligned} \phantom{AAA} , \phantom{AAA} \begin{aligned} \ell a & = (1 \ell) a \\ & = (1 \overline{a}) \ell \\ & = \overline{a} \ell \end{aligned}$$

Using this and (4) we have:

(7)$$\begin{aligned} (\ell a) b & = (\overline{a} \ell ) b \\ & = (\overline{a} \overline{b}) \ell \\ & = \ell \overline{ \overline{a} \overline{b} } \\ & = \ell (b a) \end{aligned} \phantom{AAA} , \phantom{AAA} \begin{aligned} a (b \ell) & = a (\ell \overline{b}) \\ & = \ell( \overline{a} \overline{b} ) \\ & = \overline{ \overline{a} \overline{b} } \ell \\ & = (b a) \ell \end{aligned}$$

and

(8)$$\begin{aligned} (\ell a) (\ell b) & = (\ell a) (\overline{b} \ell) \\ & = - \overline{ a \overline{b} } \\ & = - b \overline{a} \end{aligned} \phantom{AAA} , \phantom{AAA} \begin{aligned} (a \ell) (b \ell) & = (\ell \overline{a}) (b \ell) \\ & = - \overline{ \overline{a} b } \\ & = - \overline{b} a \end{aligned}$$

Equivalence of the definitions

Proposition

Definition and Definition are equivalent, in that we have an isomorphism of real star-algebras:

$$\array{ \phi & DK(A) &\overset{\simeq}{\longrightarrow}& \widetilde{DK}(A) \\ & (a,b) &\mapsto& a + \ell b }$$

Proof

It is clear from Def. that for every element $x \in \widetilde{DK}(A)$ there is a unique pair of elements $a,b \in A$ such that

$$x = a + \ell b \;=\; \phi(a,b) \,.$$

This means that $\phi$ is a linear isomorphism of the underlying real vector spaces. Hence it only remains to check that $\phi$ is indeed an algebra homomorphism and that it respects the involution.

To see that $\phi$ is an algebra homomorphism, we multiply out and then use the relations (7) and (8) from Lemma :

$$\begin{aligned} \phi(a,b) \phi(c,d) & = (a + \ell b) (c + \ell d) \\ & = a c + (\ell b)(\ell d) + a (\ell d) + (\ell b) c \\ & = a c - d \overline{b} + \ell ( \overline{a} d + c b ) \\ & = \phi(a c - d \overline{b}, \overline{a} d + c b) \end{aligned}$$

Here in the last line we indeed find the component formula (1).

To see that $\phi$ respects the involution we use (3) from Def. and (5) from Lemma :

$$\begin{aligned} \overline{\phi(a,b)} & = \overline{ a + \ell b } \\ & = \overline{a} + \overline{\ell b} \\ & = \overline{a} - \overline{b} \ell \\ & = \overline{a} - \ell b \\ & = \phi( \overline{a}, -b ) \,. \end{aligned}$$

Here in the last line we indeed find the component formula (2).

Properties

The map $a\mapsto (a,0)$ is a monomorphism $A\to A^2$. If $A$ is unital with unit $1$ then $A^2$ is unital with unit $(1,0)$. In the unital case, the element $\mathrm{i} \coloneqq (0,1)$ has the property $\mathrm{i}^2 = -1 \coloneqq (-1,0)$, and we may write $(a,b)$ as $a + b \mathrm{i}$ (while $a + \mathrm{i} b = (a,\overline{b})$). For this reason, we may write $A[\mathrm{i}]$ in place of $A^2$, at least when $A$ is unital.

Generally speaking, the double $A^2$ of an algebra $A$ has a nice property iff $A$ is one level nicer. For simplicity, assume that $A$ is unital (so that $\mathbb{R}$ is a subalgebra). Since $\overline{\mathrm{i}} = -\mathrm{i}$, we see that the involution on $A^2$ is trivial iff the involution on $A$ is trivial and $A$ further has $2 = 0$. Since $\mathrm{i} a = \overline{a} \mathrm{i}$, $A^2$ is commutative iff $A$ is commutative and the involution in $A$ is trivial. Since $a (b \mathrm{i}) = (b a) \mathrm{i}$, $A^2$ is associative iff $A$ is associative and commutative. Finally, $A^2$ is alternative iff $A$ is associative (and hence also alternative).

Examples

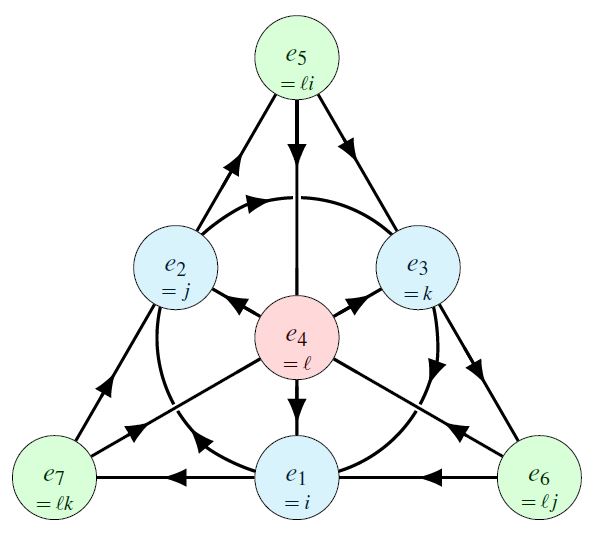
The standard example is the sequence of consecutive doubles starting with $\mathbb{R}$ itself (with the identity map as involution); these are the Cayley–Dickson algebras: the real numbers $\mathbb{R}$, the complex numbers $\mathbb{C}$, the quaternions $\mathbb{H}$, the octonions (or Cayley numbers) $\mathbb{O}$,

These are the real normed division algebras

The diagram on the right shows a basis of imaginary octonions obtained via Cayley-Dickson doubling from a standard basis $\{i,j,k\}$ of imaginary quaternions.

Next, the CD-double of the octonions is the sedenions $\mathbb{S}$, etc. , followed by further algebras which are not division algebras.
All of these algebras are power-associative, flexible, and unital, and have all inverse elements; the subalgebra with $\overline{x} = x$ is always just $\mathbb{R}$.

Related concepts

• composition algebra

References

Named after Arthur Cayley and Leonard Dickson.

The original article:

• Leonard Dickson, On Quaternions and Their Generalization and the History of the Eight Square Theorem,

  Annals of Mathematics, Second Series, Vol. 20, No. 3 (Mar., 1919), pp. 155-171 (jstor:1967865)

Review and introduction:

• M M Postnikov, Lectures on geometry, Semester V: Lie groups and Lie algebras, Lec. 14 (russian and english editions)

• John Baez, The Cayley–Dickson construction, in The octonions, Bull. Amer. Math. Soc. 39 (2002), 145-205, doi

• John Baez, This Week’s Finds — Week 59

• Tevian Dray, Corinne Manogue, Section 5.1 of: The Geomety of Octonions, World Scientific 2015 (doi:10.1142/8456)

See also

• Wikipedia, Cayley–Dickson construction

More:

• Daniel K. Biss, Daniel Dugger, Daniel Isaksen, Large annihilators in Cayley-Dickson algebras, Communications in Algebra 36 (2), 632-664, 2008 (arxiv:math/0511691)

• Daniel K. Biss, Daniel Christensen, Daniel Dugger, Daniel Isaksen, Large annihilators in Cayley-Dickson algebras II, Boletin de la Sociedad Matematica Mexicana (3) 13(2) (2007), 269-292 (arxiv:math/0702075)

• Daniel K. Biss, Daniel Christensen, Daniel Dugger, Daniel Isaksen, Eigentheory of Cayley-Dickson algebras, Forum Mathematicum 21(5) (2009), 833-851 (arxiv:0905.2987)