nLab Klein-Gordon equation
Context
Variational calculus
Differential geometric version
Derived differential geometric version
Riemannian geometry
Contents
Idea
The Klein-Gordon equation is the linear partial differential equation which is the equation of motion of a free scalar field of possibly non-vanishing mass on some (possibly curved) spacetime (Lorentzian manifold): it is the relativistic wave equation with inhomogeneity the mass .
The structure of the Klein-Gordon equation appears also in the equations of motion of richer fields than just scalar fields, where now the underlying field bundle may more generally be some vector bundle. Therefore the fundamental solutions of the Klein-Gordon equation, called the propagators (see below) pervades all of relativistic perturbative quantum field theory.
Definition
Given a spacetime (a pseudo-Riemannian manifold) and a real number , then the Klein-Gordon equation is the differential equation on smooth functions given by
where denotes the wave operator on (the analog of the Laplace operator in Lorentzian geometry) and where is for the purpose of pure PDE theory just a real number, while regarded as equipped with physical units it is the inverse Compton wavelength for mass .
This is the equation of motion of the free scalar field on , of mass and subject to a background field of gravity as encoded in the metric .
Examples
If is Minkowski spacetime equipped with its canonical coordinate functions and , then the Klein-Gordon equation reads as follows (using Einstein summation convention)
hence
Properties
Formal self-adjointness
Example
(Klein-Gordon operator is formally self-adjoint)
Let be Minkowski spacetime with Minkowski metric and let be the trivial line bundle. The canonical volume form induces an isomorphism .
Consider then the Klein-Gordon operator
This is its own formal adjoint witnessed by the bilinear differential operator given by
Proof
Bicharacteristic flow and propagation of singularities
The bicharacteristic strips of the Klein-Gordon operator are cotangent vectors along lightlike geodesics (this example).
Fundamental solutions
On a globally hyperbolic spacetime the Klein-Gordon equation has unique advanced and retarded Green functions, and respectively.
The advanced and retarded Green functions are uniquely distinguished by their support properties. Namely, only if is in the causal future of , while only if is in the causal past of .
Their difference is a bisolution known as the causal propagator, which is the Peierls bracket which gives the Poisson bracket on the covariant phase space of the free scalar field. This in turn defines the Wick algebra of the free scalar field, which yields the quantization of the free scalar field to a quantum field theory.
Other important Green functions or bisolutions include any (anti-)Feynman propagator () and Hadamard propagator. Unfortunately, it is not possible to identify them by a simple support condition. On Minkowski space, they are identified by the support of their Fourier transform. On curved spacetimes, there are two possibilities. One specifies the asymptotic expansion in a geodesically convex neighborhood of the diagonal to be of a special Hadamard form. The other specifies constraints on the wavefront set . The possibilities were proven to be equivalent in Radzikowski 96, which made essential use of the relevant notions of microlocal analysis and of distinguished parametrices introduced in DuistermaatHörmander 72.
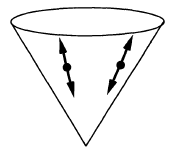
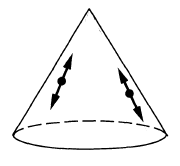
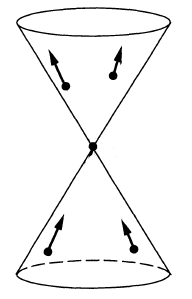
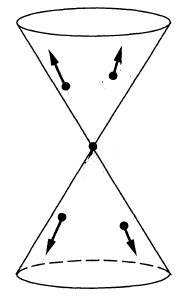
According to Radzikowski 96, the constraints on the wavefront sets of important Green functions and bisolutions can be diagrammatically illustrated as follows below. Note that the primed wavefront set of a distribution on is defined as . The diagrams illustrate tuples , where the vertex of a cone corresponds to and the cone illustrates all points linked to by null geodesics; the arrows illustrate the allowed directions of , with and linked by parallel transport and both tangent to null geodesic linking and .
propagators (i.e. integral kernels of Green functions)
for the wave operator and Klein-Gordon operator
on a globally hyperbolic spacetime such as Minkowski spacetime:
These propagators govern the construction of the Wick algebra of quantum observables of the free scalar field on the given globally hyperbolic spacetime, as well as the further deformation quantization to interacting perturbative quantum field theory on curved spacetimes via causal perturbation theory. See at locally covariant perturbative quantum field theory for more on this.
Relation to Schrödinger equation
Sometimes the Klein-Gordon equation is thought of as a relativistic refinement of the Schrödinger equation (as one passes from the non-relativistic to the relativistic particle). But this requires some care. A priori the Klein-Gordon equation takes as arguments a field on spacetime, whereas the Schrödinger equation takes as argument a wave function on phase space.
Related concepts
References
The Klein-Gordon equation is named after Oskar Klein and Walter Gordon.
Textbook account:
- James D. Bjorken, Sidney D. Drell: Relativistic Quantum Mechanics, McGrawHill (1964) [ark:/13960/t5fc2v05h, pdf, pdf]
An overview over the KG propagators on Minkowski spacetime is given in
- Mikica Kocic, Invariant Commutation and Propagation Functions Invariant Commutation and Propagation Functions (2016) [pdf]
The Hadamard propagator for the Klein-Gordon equation on general globally hyperbolic spacetimes was found in
- Marek Radzikowski, Micro-local approach to the Hadamard condition in quantum field theory on curved space-time, Commun. Math. Phys. 179 (1996), 529–553 (Euclid)
The original reference on the relevant notions of microlocal analysis and distinguished parametrices of the Klein-Gordon equation is
- Johann Duistermaat, Lars Hörmander, Fourier integral operators. II, Acta Mathematica 128 (1972), 183-269 (doi)
Textbook accounts include
-
Christian Bär, Nicolas Ginoux, Frank Pfäffle, Wave Equations on Lorentzian Manifolds and Quantization, ESI Lectures in Mathematics and Physics, European Mathematical Society Publishing House, ISBN 978-3-03719-037-1, March 2007, Softcover (arXiv:0806.1036)
-
Nicolas Ginoux, Linear wave equations, Ch. 3 in Christian Bär, Klaus Fredenhagen, Quantum Field Theory on Curved Spacetimes: Concepts and Methods, Lecture Notes in Physics, Vol. 786, Springer, 2009
See also
- Wikipedia, Klein-Gordon equation
Last revised on August 16, 2024 at 06:44:18. See the history of this page for a list of all contributions to it.