nLab McKay quiver
Context
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Graph theory
Properties
Extra properties
Extra structure
Contents
Idea
Generally, for a finite group and a linear representation of on a finite dimensional complex vector space, the McKay quiver or McKay graph associated with is the quiver whose vertices correspond to the irreducible representations of and which has edges between the th and the th vertex, for the coefficients in the expansion into irreps of the tensor product of representations of with these irreps:
Specifically this applies to the special case where SU(2) a finite subgroup of SU(2) and its defining representation on . The McKay correspondence states that in this case the corresponding McKay quivers are Dynkin quivers/Dynkin diagrams in the same ADE classification as the ADE singularity .
More precisely: If one uses all irreducible representations including the 1-dimensional trivial representation then one gets the “extended Dynkin diagram”, where the extra node corresponds to . This is the vertex indicated by a cross in the following diagrams:
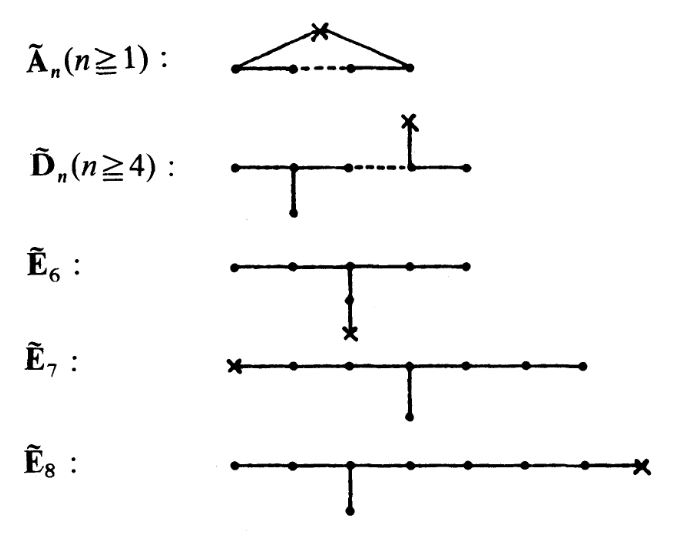
graphics grabbed from GSV 83, p. 4
In particular, for a cyclic group of order , there are complex irreps and the McKay quiver, i.e. the extended Dynkin diagram, has -vertices, connected by edges to form a circle.
Related concepts
References
The construction is due to
- John McKay, Graphs, singularities, and finite groups Proc. Symp. Pure Math. Vol. 37. No. 183. 1980
Interpretation in terms of equivariant K-theory of the corresponding ADE-singularity and plain K-theory of its blowup is due to
- Gérard Gonzalez-Sprinberg, Jean-Louis Verdier, p. 4 fo Construction géométrique de la correspondance de McKay, Ann. Sci. ́École Norm. Sup.16 (1983) 409–449. (numdam)
See also
- Wikipedia, McKay graph
Last revised on April 14, 2025 at 03:39:57. See the history of this page for a list of all contributions to it.