nLab Dynkin quiver
Context
Graph theory
Properties
Extra properties
Extra structure
Representation theory
geometric representation theory
Ingredients
Definitions
representation, 2-representation, ∞-representation
Geometric representation theory
-
Grothendieck group, lambda-ring, symmetric function, formal group
-
principal bundle, torsor, vector bundle, Atiyah Lie algebroid
-
Eilenberg-Moore category, algebra over an operad, actegory, crossed module
Theorems
Contents
Definition
A Dynkin quiver is a quiver whose underlying undirected graph is a one of the Dynkin diagrams in the ADE series.
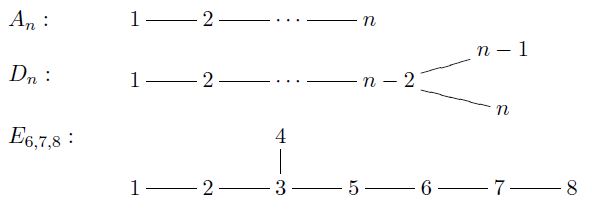
graphics grabbed from Qiu 15
See e.g. Qiu 15, Def. 2.1
Properties
Characterization as finite-type quivers
Gabriel's theorem (Gabriel 72) says that connected quivers with a finite number of indecomposable quiver representations over an algebraically closed field are precisely the Dynkin quivers: those whose underlying undirected graph is a Dynkin diagram in the ADE series
Moreover, the indecomposable quiver representations in this case are bijection with the positive roots in the root system of the Dynkin diagram.
McKay correspondence
ADE classification and McKay correspondence
References
Gabriel's theorem is due to
- Peter Gabriel, Unzerlegbare Darstellungen. I, Manuscripta Mathematica 6: 71–103, (1972)
Discussion of Bridgeland stability conditions on quiver representations over Dynkin Quivers includes
-
Yu Qiu, Stability conditions and quantum dilogarithm identities for Dynkin quivers, Adv. Math., 269 (2015), pp 220-264 (arXiv:1111.1010)
-
Tom Bridgeland, Yu Qiu, Tom Sutherland, Stability conditions and the quiver (arXiv:1406.2566)
Last revised on October 2, 2018 at 15:47:04. See the history of this page for a list of all contributions to it.