nLab induced representation

Idea

Given a group $G$ with subgroup $H \xhookrightarrow{\iota} G$ then the evident operation $\iota^\ast$ of restricting linear representations of $G$ to $H$-representations has both a left adjoint $i_!$ (2) and a right adjoint $i_\ast$ functor (5). For $V \in H Rep$, the image $i_! V \in G Rep$ is called the left induced representation and the image $i_\ast V \in G Rep$ is called the right induced representation or co-induced representation of $V$.

Often this is considered for finite groups or at least for subgroups of finite index, in which case these left and right adjoints agree to make an ambidextrous adjunction (Prop. ) and then are both traditionally denoted $ind_H^G V$ and just called the induced representation. The hom-isomorphism of the adjunction in this case is traditionally known as Frobenius reciprocity.

Definition

Traditional formulation

Consider:

• $G$ a group,

• $\mathbb{K}$ a ground field (or ground ring),

• $\mathbb{K}[G] \,\coloneqq\, Span_{\mathbb{K}}\big( g \in G \big)$ the $\mathbb{K}$-linear span of the elements of $G$, hence with linear basis $G \subset \mathbb{K}[G]$, and equipped with the structure of the group algebra of $G$ over $\mathbb{K}$, to be regarded canonically as a module (bimodule) over itself,

• $G Rep_{\mathbb{K}} \,\simeq\, \mathbb{K}[G]\text{-}Mod_{\mathbb{K}}$ the category of $\mathbb{K}$-linear representations $G \curvearrowright V$ of $G$,

  $$\begin{array}{ccc} G \times V &\longrightarrow& V \\ (g,v) &\mapsto& g \cdot v \mathrlap{\,,} \end{array}$$

  with intertwiners between them as morphisms,

  equivalently the category of $\mathbb{K}[G]$-modules, with hom-spaces to be denoted

  $$Hom_G(-,-) \,\equiv\, Hom_{\mathbb{K}[G]}(-,-) \mathrlap{\,,}$$

• $H \xhookrightarrow{\iota} G$ a subgroup inclusion.

Write

(1)$$\iota^\ast \;\colon\; G Rep_{\mathbb{K}} \xrightarrow{\;} H Rep_{\mathbb{K}}$$

for the functor forming restricted representations along $\iota \colon H \hookrightarrow G$ (letting $H$ act on a given $G$-representation via its inclusion $\iota$ into $G$).

Proposition

(left induced representation) The functor $\iota^\ast$ (1) has a left adjoint $\iota_! \colon H Rep_{\mathbb{K}} \xrightarrow{\;} G Rep_{\mathbb{K}}$ given by

(2)$$V \in H Rep_{\mathbb{K}} \;\;\;\;\;\; \vdash \;\;\;\;\;\; \iota_{!} V \;\coloneqq\; \mathbb{K}[G] \otimes_{\mathbb{K}[H]} V \,,$$

where on the right we have the $\mathbb{K}$-vector space (or $\mathbb{K}$-module) underlying the tensor product of (right-with-left) $\mathbb{K}[H]$-modules equipped with the $G$-group action given by

(3)$$\left. \begin{array}{l} [a,v] \,\in\, \mathbb{K}[G] \otimes_{\mathbb{K}[H]} V \\ g \,\in\, G \end{array} \right\} \;\;\;\;\;\; \vdash \;\;\;\;\;\; g \cdot [a,v] \,\coloneqq\, [g \cdot a, v] \,.$$

Proof

We claim that the hom-isomorphism is given by evaluation at the neutral element $\mathrm{e} \in G$:

(4)$$\left. \begin{array}{l} V \,\in\, H Rep_{\mathbb{K}} \\ W \,\in\, G Rep_{\mathbb{K}} \end{array} \right\} \;\;\;\;\; \vdash \;\;\;\;\; \frac{ \overset{ \iota_! V }{ \overbrace{ \mathbb{K}[G] \otimes_{\mathbb{K}[H]} V } } \xrightarrow{\;\; f \;\;} W }{ V \xrightarrow{ f([\mathrm{e},-]) } \iota^\ast W \mathrlap{\,.} }$$

To see this, just observe that

$$\left. \begin{array}{l} f \,\in\, Hom_G\big( \mathbb{K}[G] \otimes_{\mathbb{K}[H]} V ,\, W \big) \\ h \,\in\, H \\ v \,\in\, V \end{array} \right\} \;\;\;\;\; \vdash \;\;\;\;\; \begin{array}{rcl} f\big( [\mathrm{e}, h \cdot v] \big) &=& f\big( [\mathrm{e} \cdot h, v] \big) \;=\; f\big( [h, v] \big) \\ &=& f\big( [h \cdot \mathrm{e}, v] \big) \;=\; f\big( h \cdot [\mathrm{e}, v] \big) \;=\; h \cdot \Big( f\big( [\mathrm{e}, v] \big) \Big) \mathrlap{\,,} \end{array}$$

where the first equality is by definition of the tensor product, the second-but-last is (3) and the last one is by the $G$-equivariance of $f$. This shows that $f\big([\mathrm{e},-]\big)$ is $H$-equivariant and that it uniquely determines $f$, hence that we have a bijection of hom-sets

$$Hom_G\Big( \mathbb{K}[G] \otimes_{\mathbb{K}[H]} V ,\, W \Big) \;\;\simeq\;\; Hom_H\Big( V ,\, \iota^\ast W \Big) \,.$$

Finally, it is manifest that this bijection $f \mapsto f([\mathrm{e},-])$ is natural in $V$ and $W$, and so this establishes a hom-isomorphism exhibiting the claimed adjunction $\iota_! \dashv \iota^\ast$.

Corollary

The counit $\eta^{L}$ of the left adjunction $\iota_! \dashv \iota^\ast$ (Prop. ) is given by inserting the neutral element:

$$\begin{array}{rcc} V &\xrightarrow{\phantom{--} \epsilon^L_V \phantom{--}}& \mathbb{K}[G] \otimes_{\mathbb{K}[H]} V \\ v &\mapsto& [\mathrm{e},v] \end{array}$$

Proof

The adjunction unit is (see there) the adjunct $\widetilde{(-)}$ of the identity map:

$$\begin{array}{rcl} \mathbb{K}[G] \otimes_{\mathbb{K}[H]} V &\xrightarrow{\phantom{--} id \phantom{--}}& \mathbb{K}[G] \otimes_{\mathbb{K}[H]} V \mathrlap{\,,} \end{array}$$

hence is its image $\widetilde{id}$ under the hom-isomorphism (4). From that formula (4) we have indeed

$$\widetilde{id}(v) \;=\; id([\mathrm{e},v]) \;=\; [\mathrm{e},v] \,.$$

Proposition

(right induced representation) The functor $\iota^\ast$ (1) has a right adjoint $\iota_\ast \colon H Rep_{\mathbb{K}} \xrightarrow{\;} G Rep_{\mathbb{K}}$ given by

(5)$$V \in H Rep_{\mathbb{K}} \;\;\;\;\;\; \vdash \;\;\;\;\;\; \iota_{\ast} V \;\coloneqq\; hom_H\big( \mathbb{K}[G] ,\, V \big) \mathrlap{\,,}$$

where on the right we have the $\mathbb{K}$-vector space (or $\mathbb{K}$-module) of $H$-equivariant $\mathbb{K}$-linear maps equipped with the $G$-group action given by

(6)$$\left. \begin{array}{l} f \,\colon\, \mathbb{K}[G] \xrightarrow{\;} V \\ g \,\in\, G \\ a \,\in\, \mathbb{K}[G] \end{array} \right\} \;\;\;\;\;\; \vdash \;\;\;\;\;\; (g \cdot f)(a) \,\coloneqq\, f(a \cdot g) \,.$$

Proof

We claim that the hom-isomorphism is given by evaluation at the neutral element $\mathrm{e} \in G$:

(7)$$\left. \begin{array}{l} V \,\in\, H Rep_{\mathbb{K}} \\ W \,\in\, G Rep_{\mathbb{K}} \end{array} \right\} \;\;\;\;\;\;\;\; \vdash \;\;\;\;\;\;\;\; \frac{ W \xrightarrow{\;\;\;\; f \;\;\;\;} \overset{\iota_\ast V}{ \overbrace{ hom_{H}\big( \mathbb{K}[G] ,\, V \big) } } }{ \iota^\ast W \xrightarrow{\;\; f(-)(\mathrm{e}) \;\;} V \mathrlap{\,.} }$$

To see this, just observe that

$$\left. \begin{array}{l} f \,\in\, Hom_G\Big( W ,\, hom_H\big( \mathbb{K}[G] ,\, V \big) \Big) \\ h \,\in\, H \\ w \,\in\, W \end{array} \right\} \;\;\;\;\;\; \vdash \;\;\;\;\;\; \begin{array}{rcl} f(h \cdot w)(\mathrm{e}) &=& \big( h \cdot f(w) \big)(\mathrm{e}) \;=\; f(w)(\mathrm{e} \cdot h) \;=\; f(w)(h) \\ &=& f(w)(h \cdot \mathrm{e}) \;=\; h\cdot\big(f(w)(\mathrm{e})\big) \mathrlap{\,,} \end{array}$$

where the first equality is the $G$-equivariance of $f$, the second is (6) and the last one is the $H$-equivariance of $f(w)$. This shows that $f(-)(\mathrm{e})$ is $H$-equivariant and that it uniquely determines $f$, hence that we have a bijection of hom-sets:

$$Hom_G\Big( W ,\, hom_H\big( \mathbb{K}[G] ,\, V \big) \Big) \;\;\simeq\;\; Hom_H\big( \iota^\ast W ,\, V \big) \mathrlap{\,.}$$

Finally, it is manifest that this bijection $f \mapsto f([\mathrm{e},-])$ is natural in $W$ and $V$, and so this establishes a hom-isomorphism exhibiting the claimed adjunction $\iota^\ast \dashv \iota_{\ast}$.

Corollary

The counit $\epsilon^{R}$ of the right adjunction $\iota^\ast \dashv \iota_\ast$ (Prop. ) is given by evaluation at the neutral element:

$$\begin{array}{rcc} hom_H\big( \mathbb{K}[G] ,\, V \big) &\xrightarrow{\phantom{--} \epsilon^R_V \phantom{--}}& V \\ \phi &\mapsto& \phi(\mathrm{e}) \end{array}$$

Proof

The adjunction counit is (see there) the adjunct $\widetilde{(-)}$ of the identity map:

$$\begin{array}{rcl} hom_H\big( \mathbb{K}[G] ,\, V \big) &\xrightarrow{\phantom{--} id \phantom{--}}& hom_H\big( \mathbb{K}[G] ,\, V \big) \mathrlap{\,,} \end{array}$$

hence is its image $\widetilde{id}$ under the hom-isomorphism (7). From that formula (7) we have indeed

$$\widetilde{id}(\phi) \;=\; id(\phi)(\mathrm{e}) \;=\; \phi(\mathrm{e}) \,.$$

Groupoid formulation

A first step towards a deeper understanding for what’s going on with induced representations above is to resolve the subgroup inclusion $H \xhookrightarrow{\iota} G$ to a (Kan) fibration of groupoids, which will show that left/right induced representations are about forming (direct) sums/products of contributions over the homotopy fiber of $\mathbf{B}\iota$.

To that end, recall for any group action $G \curvearrowright S$ on a set $S$ the action groupoid

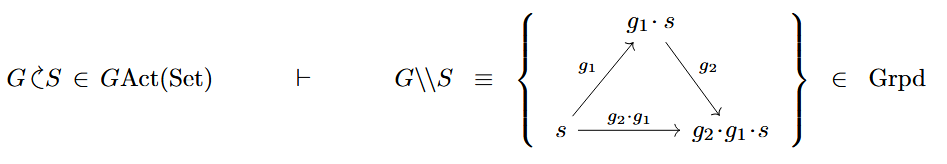
Examples are delooping groupoids $\mathbf{B}G$ and “homotopy double coset groupoids” like $G \backslash\!\backslash G\!/\!H$:

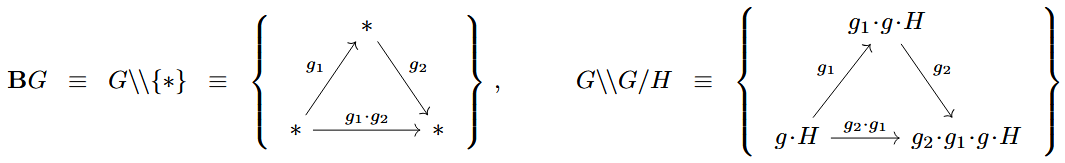
where our variance convention is such that functors $\mathbf{B}G \xrightarrow{\;} \mathcal{C}$ are equivalent to left group actions in $\mathcal{C}$, and in particular functors $\mathbf{B}G \xrightarrow{\;} Vec$ are directly identified with linear representations of $G$:

$$Func(\mathbf{B}G,\, Vec) \;\simeq\; G Rep \,.$$

Accordingly, for $\mathcal{G} \in Grpd$ any groupoid, functors $\mathcal{G} \xrightarrow{\;} Vec$ are linear groupoid representations.

Lemma

For $H \xhookrightarrow{\iota} G$ a subgroup inclusion:

1. the homotopy double coset groupoid $G \backslash\!\backslash G\!/\!H$ is equivalent to the delooping groupoid of $H$:

   $$\mathbf{B}H \,\simeq\, G \backslash\!\backslash G\!/\!H \,,$$

2. such that the canonical functor

   (8)$$G \backslash\!\backslash G\!/\!H \xrightarrow{\phantom{--\widehat{\mathbf{B}\iota}--}} G \backslash\!\backslash \{\ast\} \,\simeq\, \mathbf{B}G$$

   is a resolution of $\mathbf{B}\iota \,\colon\, \mathbf{B}H \xrightarrow{\;} \mathbf{B}G$ by a surjective Kan fibration,

   thus exhibiting its ordinary fiber $G\!/\!H$ as the homotopy fiber of $\mathbf{B}\iota$,

3. the induced equivalence of representation-categories

   $$H Rep \;\simeq\; Func(\mathbf{B}H,\,Vect) \;\simeq\; Func(G \backslash\!\backslash G\!/\!H,\,Vect)$$

   is exhibited by sending a given $G$-representation $\mathscr{V}$ to the groupoid representation $\widehat{\mathscr{V}}$ given by

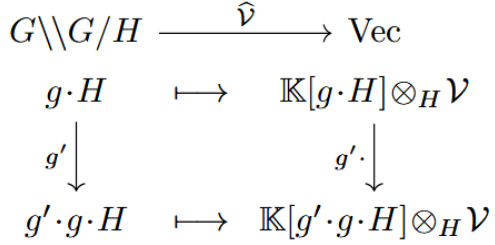
Note that $g \cdot H$ on the left is (the name of) an object of the groupoid $G \backslash\!\backslash G\!/\!H$, while on the right it is the actual set of right $H$-translates of the element $g$.

Proof

The following functor is evidently both essentially surjective as well as fully faithful, therefore is an equivalence of groupoids:

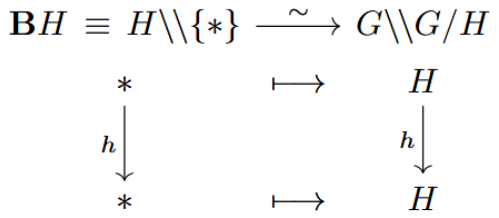
The claim that this factors $\mathbf{B}\iota$ through a surjective Kan fibration is now immediate from inspection.

Moreover, the following inspection shows that the claimed operation $\widehat{(-)}$ extends to a functor which is a strict right inverse to precomposition with the previous resolution functor:

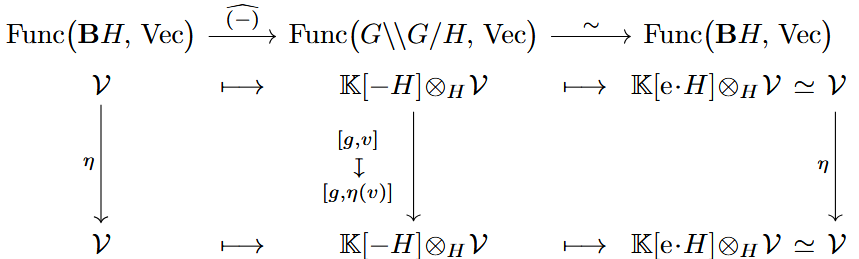
(To note here that the natural transformation in the middle is indeed well-defined, due to the the intertwining-property of the homomorphism $\eta$ of linear representations.)

Hence by the 2-out-of-3-property enjoyed by equivalences of groupoids (cf. the canonical model structure on groupoids) it follows that $\widehat{(-)}$ is an equivalence, as claimed.

With this in hand we have an equivalent but “more obvious” re-statement of the existence of left induced representations (2):

Proposition

(resolved left induced representation) The functor $\widehat{\mathbf{B}\iota}$ (8) has a left adjoint $\big(\widehat{\mathbf{B}\iota}\big)_! \,\colon\, Func\big( G \sslash\!\sslash G/H ,\, Vect \big) \longrightarrow Func\big(G \sslash\!\sslash \{\ast\},\, Vect\big)$ given by

(9)$$\mathscr{V} \,\in\, Func\big( G \backslash\!\backslash G/H \big) \;\;\;\;\;\;\;\;\; \vdash \;\;\;\;\;\;\;\;\; \big(\widehat{\mathbf{B}\iota}\big)_! \mathscr{V} \;\coloneqq\; \underset{ g\cdot H }{\bigoplus} \mathscr{V}_{g\cdot H} \,,$$

where on the right we let $G$ act in the evident way between direct summands.

Proof

The hom-isomorphism is essentially tautologous:

$$\left. \begin{array}{l} \mathscr{V} \,\in\, Func\big( G\backslash\!\backslash G/H, Vect\big) \\ \mathscr{W} \,\in\, Func\big( G\backslash\!\backslash \{\ast\}, Vect\big) \end{array} \right\} \;\;\;\;\;\;\;\; \vdash \;\;\;\;\;\;\;\; \frac{ \Big( \displaystyle{ \underset{ g\cdot H \in G/H }{\bigoplus} \mathscr{V}_{{}_{g\cdot H}} } \Big) \xrightarrow{ \Big( f_{{}_{g \cdot H}} \Big)_{g \cdot H \in G/H} } \mathscr{W} }{ g\cdot H \;\;\;\vdash\;\;\; \mathscr{V}_{g \cdot H} \xrightarrow{\;\; f_{g \cdot H} \;\;} \mathscr{V} \mathrlap{\,,} }$$

where we don’t display the $G$-action, which is however evident and evidently respected.

Corollary

Under the identification of $H$-representations $\mathscr{V}$ with groupoid representations $\widehat{\mathscr{V}}$ according to Prop. , their left induced representations (9) are simply the direct sum of the contributions of $\widehat{\mathscr{V}}$ over the homotopy fiber $G/H$ of $\mathbf{B}\iota$:

$$\big(\widehat{\mathbf{B}\iota}\big)_! \widehat{\mathscr{V}} \;\; \equiv \;\; \underset{ g\cdot H \in G/H }{\bigoplus} \widehat{\mathscr{V}}_{g \cdot H} \;\; \simeq \;\; \underset{ g\cdot H \in G/H }{\bigoplus} \mathbb{K}[g\!\cdot\!H] \otimes_H \mathscr{V} \;\;\simeq\;\; \mathbb{K}[G]\otimes_H \mathscr{V} \;\;\equiv\;\; \iota_! \mathscr{V}$$

General abstract formulation

We formulate induction and coinduction of representations abstractly in homotopy type theory. (Hence the following is automatically the (∞,1)-category theory-version, which in parts is sometimes referred to as cohomological induction.)

Let $\mathbf{H}$ be an ambient (∞,1)-topos. By the discussion at ∞-action, for $G \in Grp(\mathbf{H})$ a group object in $\mathbf{H}$, hence an ∞-group, the slice (∞,1)-topos $\mathbf{H}_{/\mathbf{B}G}$ over its delooping is the (∞,1)-category of $G$-∞-actions

$$Act(G) \simeq \mathbf{H}_{/\mathbf{B}G} \,.$$

(A genuine ∞-representation/∞-module over $G$ may be taken to be a an abelian $\infty$-group object in $Act(G)$, but we can just as well work in the more general context of possibly non-linear representations, hence of actions.)

Accordingly, for $f \colon H \to G$ a homomorphism of ∞-groups, hence for a morphism $\mathbf{B}f \colon \mathbf{B}H \to \mathbf{B}G$ of their deloopings, there is the corresponding base change geometric morphism

$$\textstyle{\big(\sum_f \dashv f^* \dashv \prod_f\big)} \;\colon\; Act(H) \stackrel{\overset{\sum_f}{\to}}{\stackrel{\overset{f^*}{\leftarrow}}{\underset{\prod_f}{\to}}} Act(G) \,.$$

Here

• the inverse image/(∞,1)-pullback functor $f^*$ produces the “restricted” $\infty$-representations along $f$;

• the dependent sum $\sum_f$ is the induced representation ∞-functor;

• the dependent product $\prod_f$ is the coinduced representation ∞-functor.

For the case of permutation representations of discrete groups this perspective is made explicit by Lawvere 1969 p. 14, 1970 p. 5.

Properties

Ambidexterity

We show that for subgroup inclusions of finite index the left and right induced representations (above) agree.

Lemma

(comparison map between left and right induced representations)
For $H \xhookrightarrow{\;} G$ a subgroup inclusion and $V \in H Rep$, we have a $G$-equivariant linear injection from the left (2) into the right induced representation (5)

$$\mathbb{K}[G] \otimes_{\mathbb{K}[H]} V \xhookrightarrow{\phantom{--}\phi\phantom{--}} hom_H\big( \mathbb{K}[G] ,\, V \big) \mathrlap{\,,}$$

natural in $V$, which is an isomorphism if the subgroup inclusion $H \hookrightarrow G$ has finite index.

Proof

Define $\phi$ to take homogeneous elements of the form $[g,v]$, for $g \in G \subset \mathbb{K}[G]$, to the linear map $\phi[g,v] \,\colon\, \mathbb{K}[G] \to V$ which, in turn, is given on basis elements $g' \in G \subset \mathbb{K}[G]$ by

$$\phi[g,v] \;\colon\; g' \;\mapsto\; \left\{ \begin{array}{lll} h \cdot v &\vert& g' = h \cdot g^{-1} \\ 0 &\vert& \text{otherwise} \end{array} \right.$$

First to observe that this construction is well defined, in that

1. $\phi[g,v]$ is $H$-equivariant,

   which is immediate from the form of the above formula;

2. $\phi$ is independent of the choice of representative $[g,v] = [g \cdot k, k^{-1}\cdot v]$,

   which is seen from

   $$\phi[g \cdot k, k^{-1} \cdot v] \;\colon\; g' \;\mapsto\; \left\{ \begin{array}{lll} h \cdot k^{-1} \cdot v &\vert& g' = h \cdot (g \cdot k)^{-1} = h \cdot k^{-1} \cdot g^{-1} \\ 0 &\vert& \text{otherwise} \end{array} \right.$$

   whence indeed $\phi[g \cdot k, k^{-1} \cdot v] \;=\; \phi[g,v] \,;$

3. $\phi$ is $G$-equivariant,

   which is seen by computing for $q \in G$ as follows:

   $$\begin{array}{rcl} \phi\big( q \cdot [g,v] \big)(g') &\equiv& \phi\big( [q \cdot g,v] \big)(g') \\ &=& \left\{ \begin{array}{rcl} h \cdot v &\vert& g' = h \cdot (q\cdot g)^{-1} \\ 0 &\vert& \text{otherwise} \end{array} \right. \\ &=& \left\{ \begin{array}{rcl} h \cdot v &\vert& g' \cdot q = h \cdot g^{-1} \\ 0 &\vert& \text{otherwise} \end{array} \right. \\ &=& (\phi[g,v])(g' \cdot q) \\ &\equiv& \big( q \cdot \phi[g,v] \big)(g') \mathrlap{\,.} \end{array}$$

It is also immediate that the construction is natural in $V$.

Now the $H$-equivariance implies that for any choice of section $[g] \mapsto g$ of the coset quotient coprojection $G \twoheadrightarrow G/H$ (in Sets) the range of $\phi$ is spanned by the combinations $\sum_{[g] \in G/H} \phi[g,v_g]$.

For this to vanish on all $g'$ clearly all the $v_g$ must vanish separately, which shows that the kernel of $\phi$ is $0$, hence that we have an injection.

At the same time, if $H$ has finite index in $G$ then both this range as well as the codomain $hom_H\big( \mathbb{K}[G] ,\, V \big)$ have finite dimension, both equal to the number ${\vert G \colon H\vert}$ of $H$-cosets of elements of $G$. This means (by the rank-nullity theorem, if you wish) that in the case of finite index the injection $\phi$ is moreover surjective and hence an isomorphism, as claimed.

Hence:

Proposition

(induction along finite-index inclusions is ambidextrous)
When the subgroup inclusion $H \xhookrightarrow{\iota} G$ has finite index (in particular if $G$ is already a finite group) then the left (2) and right induced representation functors (5) are naturally isomorphic $\iota_! \simeq \iota_{\ast}$, constituting with $\iota^\ast$ an ambidextrous adjunction.

Proof

By Lem. .

This statement is mentioned for instance in Hristova 2019 p 1.

The situation generalizes to representations of Hopf algebras, cf. Flake et al. 2024.

Further

Proposition

(Brauer induction theorem)
Over the complex numbers, the virtual representations of a finite group are all virtual combinations of induced representations of 1-dimensional representations.

Examples and Applications

Basic examples

Example

if $V = \mathbf{1}$ is the trivial representation of dimension 1 then its induced representation is the basic permutation representation spanned by the coset-space $G/H$:

$$ind_H^G \left( \mathbf{1} \right) \;=\; k[G/H] \,.$$

For more see at induced representation of the trivial representation.

(cf. tom Dieck 2009, Chapter 4)

Centralizer algebra / Hecke algebra

Let

$$i \colon H \hookrightarrow G$$

be a group homomorphism (often assumed to be a subgroup inclusion, and sometimes with $G$ assumed to be a finite group). For $E \in H Rep$ some $H$-representation (often taken to be the trivial $H$-representation), let $Ind_i E \in G Rep$ be the induced $G$-representation. Then the endomorphism ring $End_G(Ind_i E)$ of $Ind_i E$ in $G Rep$ is called the centralizer algebra or also the Hecke algebra or Iwahori-Hecke algebra? $Hecke(E,i)$ of the induced representation. (Basics are in Woit, def. 2, details are in Curtis & Reiner 1981, section 67, a quick survey of related theory is given by Srinivasan.

In terms of the notation in General abstract formulation above and for $i \colon H \to G$ any homomorphism of $\infty$-groups, we have the ∞-monoid

$$Hecke(E,i) \;\coloneqq\; \textstyle{ \underset{\mathbf{B}G}{\prod} \left[ \underset{\mathbf{B}i}{\sum} E ,\, \underset{\mathbf{B}i}{\sum} E \right] } \,,$$

where $[-,-]$ is the internal hom in the slice (∞,1)-topos $\mathbf{H}_{/\mathbf{B}G} \simeq G Act(\mathbf{H})$.

For $V \in Act(G)$ any other representation, there is a canonical ∞-action of $Hecke(E,i)$ on $\underset{\mathbf{B}G}{\prod} \left[\underset{\mathbf{B}i}{\sum} E , V \right]$. If here $E$ is the trivial representation then by adjointness this is the invariants $V^G$ of $V$ and hence the Hecke algebra acts on the invariants. (See for instance Woit, def. 2). This is sometimes called the Hecke algebra action on the Iwahori fixed vectors (e.g. here, p. 9)

Zuckerman functors: Coinduction on Harish-Chandra modules

Coinduction on Harish-Chandra modules is referred to as Zuckerman induction. See there for more details.

Related concepts

• The identification of representation induction as the extra left adjoint in a base change morphism, as discussed in the General abstract discussion above, puts induced representations in the same general abstract framework as existential quantification in logic and generally of dependent sum in dependent type theory (see there for more details). This relation has first been amplified in (Lawvere).

• If the modules over a group are considered as comodules over the function Hopf algebra over the group, then one can instead consider the induction for comodules. See cotensor product.

• The derived functor of the representation induction functor is often referred to as cohomological induction.

• Dirac induction

• The character of an induced representation is an induced character.

• Artin induction theorem

• Brauer induction theorem

• Artin-Lam induction exponent

representation theory and equivariant cohomology in terms of (∞,1)-topos theory/homotopy type theory (FSS 12 I, exmp. 4.4):

homotopy type theory	representation theory
pointed connected context $\mathbf{B}G$	∞-group $G$
dependent type on $\mathbf{B}G$	$G$-∞-action/∞-representation
dependent sum along $\mathbf{B}G \to \ast$	coinvariants/homotopy quotient
context extension along $\mathbf{B}G \to \ast$	trivial representation
dependent product along $\mathbf{B}G \to \ast$	homotopy invariants/∞-group cohomology
dependent product of internal hom along $\mathbf{B}G \to \ast$	equivariant cohomology
dependent sum along $\mathbf{B}G \to \mathbf{B}H$	induced representation
context extension along $\mathbf{B}G \to \mathbf{B}H$	restricted representation
dependent product along $\mathbf{B}G \to \mathbf{B}H$	coinduced representation
spectrum object in context $\mathbf{B}G$	spectrum with G-action (naive G-spectrum)

References

Traditional formulation

Original articles:

• George Mackey, Induced representations of locally compact groups I, Annals of Mathematics 55 1 (1952) 101-139 [doi:10.2307/1969423, jstor:1969423]

• George Mackey: Induced representations of locally compact groups II, Annals of Mathematics 58 2 (1953) 193-221 [doi:10.2307/1969786, jstor:1969786]

• George Mackey: Induced representations of groups and quantum mechanics, W. A. Benjamin, New York (1968) [ark:/13960/t6841m201]

  (cf. Wigner classification)

Textbook accounts:

• Jean-Pierre Serre, section 3.3 of: Linear Representations of Finite Groups, Graduate Texts in Mathematics 42, Springer (1977) [doi:10.1007/978-1-4684-9458-7, pdf]

• Charles Curtis, Irving Reiner: Induced Representations, chapter VII in: Representation theory of finite groups and associative algebras, AMS (1962) [ISBN:978-0-8218-4066-5]

• Charles Curtis, Irving Reiner: Methods of representation theory – With applications to finite groups and orders – Vol. I, Wiley (1981) [ark:/13960/t8gf4wd3x]

• William Fulton, Joe Harris, section 3.3 of: Representation Theory: a First Course, Springer (1991) [doi:10.1007/978-1-4612-0979-9]

• Pavel Etingof, Dmitry Vaintrob, et al., section 4.8 of: Introduction to representation theory, Student Mathematical Library 59, AMS (2011) [arXiv:0901.0827, ams:stml-59]

• Benjamin Steinberg, section 8.2 of: Representation Theory of Finite Groups – An Introductory Approach, Springer (2012) [doi:10.1007/978-1-4614-0776-8]

Lecture notes:

• Tammo tom Dieck, Chapter 4 of Representation theory (2009) [pdf]

See also:

• Wikipedia: Induced representation

• eom: induced representation

• Wrong-way Frobenius reciprocity for finite groups representations [MO:q/132272]

• Bhama Srinivasan; Modular Representations, Old and New, [pdf, pdf]

For Hopf algebras

• Johannes Flake, Robert Laugwitz, Sebastian Posur: Frobenius monoidal functors induced by Frobenius extensions of Hopf algebras [arXiv:2412.15056]

General abstract formulation

The general abstract formulation above is mentioned (for discrete groups and their permutation representations) in

• William Lawvere: Adjointness in Foundations, Dialectica 23 (1969) 281-296, Reprints in Theory and Applications of Categories, 16 (2006) 1-16 [pdf]

• William Lawvere: Equality in hyperdoctrines and comprehension schema as an adjoint functor, Proceedings of the AMS Symposium on Pure Mathematics XVII (1970) 1-14 [pdf]