nLab Yang-Baxter equation

Idea

A Yang-Baxter equation (YBE) is, in some form or other, an algebraic reflection of this isotopy of braids:

(1)

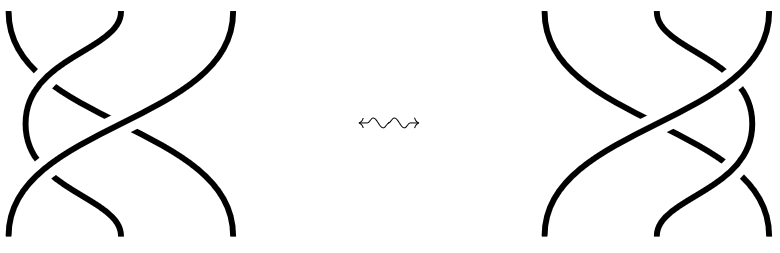
which is also known as the 2nd Artin braid relation or the 3rd Reidemeister move for framed links.

Quantum YBE

Plain form

Interpreting the isotopy (1) as an equality of string diagrams in a braided monoidal category $(\mathcal{C}, \otimes)$, with each strand/string labeled by the same given object $V \in \mathcal{C}$, it says that the braiding $R \colon\, V \otimes V \to V \otimes V$ satisfies

(2)$$(R \otimes id) \circ (id \otimes R) \circ (R \otimes id) \;\; = \;\; (id \otimes R) \circ (R \otimes id) \circ (id \otimes R)$$

as an equation in $End(V \otimes V \otimes V)$ (where we are notationally suppressing associators, in full this is diagram B7 in Joyal & Street 1985 p 7).

This equation (2) — on any map $R$ of the form $R \,\colon\, V \otimes V \to V \otimes V$ (not necessarily the ambient braiding structure map) — is called the plain quantum Yang-Baxter equation.

If $V \otimes V$ is the tensor product of a finite-dimensional vector space $V$ with itself, then any choice of linear basis $V \simeq k^d$ identifies the linear map $R$ with a matrix $(R_{n_1, n_2}^{m_1, m_2})_{n_i, m_i = 1}^{d}$, thus traditionally called an R-matrix.

In a symmetric monoidal category like $Vect$, with symmetric braiding $\sigma \,\colon\, V \otimes V \to V \otimes V$, it is traditional to define

$$\check R \,\coloneqq\, \sigma \circ R \;\;\;\; \text{and} \;\;\;\; \check R_{i j} \,\coloneqq\, \phi_{i,j}(\sigma \circ R) \mathrlap{\,,}$$

where

$$\phi_{i,j} \,\colon\, End(V \otimes V) \hookrightarrow End(V \otimes V \otimes V) \;\;\;\;\; \text{for} \; 1 \leq i \lt j \leq 3$$

identifies $V \otimes V$ with the tensor product of the $i$th and the $j$th copy of $V$ in $V \otimes V \otimes V$ (inserting an identity on the remaining copy).

In terms of this “check-R matrix” $\check R$, the plain quantum Yang-Baxter equation (2) is equivalent to

(3)$$\check R_{23} \circ \check R_{13} \circ \check R_{12} \;=\; \check R_{12} \circ \check R_{13} \circ \check R_{23} \,.$$

Braid representations. In either form, any solution to the plain Yang-Baxter equation in $Vect$ defines linear representations of the braid groups $Br_n$ (braid representations), by representing the $i$th Artin braid generator $b_i$ by

$$b_i \;\; \mapsto \;\; id^{\otimes_{i-1}} \otimes R \otimes id^{\otimes_{n-i-1}} \,.$$

This is manifest from the Artin presentation of the braid group, see there.

If, in addition, the $R$-matrix is involutive in that $R \circ R = id$, then these braid representations actually are (factor through) representations of the symmetric group $Sym_n$.

Parameterized form

The plain form (3) of the Yang-Baxter equation generalizes to the case where $\check R_{i j}$ is taken to dependent on a pair of parameters $u, u' \in U$ (typically taken from $U = \mathbb{C}$ the complex numbers), in which case one says that the condition

(4)$$\check R_{23}(u_2, u_3) \circ \check R_{13}(u_1, u_3) \circ \check R_{12}(u_1, u_2) \;=\; \check R_{12}(u_1, u_2) \circ \check R_{13}(u_1, u_3) \circ \check R_{23}(u_2, u_3)$$

is the parameterized quantum Yang-Baxter equation.

In the special case of this generalization where $U \equiv \mathbb{C}^\times$ is the multiplicative group of complex numbers and restricting the dependence to be on the quotient of the parameters

$$\check R(u, u') \,=\, \check R( u/u') \,,$$

the parameterized quantum Yang-Baxter equation (4) becomes (identifying $u \coloneqq u_1/u_2$ and $v \coloneqq u_2/u_3$)

(5)$$\check R_{23}(v) \circ \check R_{13}(u v) \circ \check R_{12}(u) \;=\; \check R_{12}(u) \circ \check R_{13}(u v) \circ \check R_{23}(v) \,,$$

and one speaks of the parameterized quantum Yang-Baxter equation with “multiplicative spectral parameter”.

Yet again redefining by passage to logarithms of the parameters, $u \mapsto ln u$ (or rather, understanding the previous parameters a exponentials), the equation (6) assumes the form with “additive spectral parameter”:

(6)$$\check R_{23}(v) \circ \check R_{13}(u + v) \circ \check R_{12}(u) \;=\; \check R_{12}(u) \circ \check R_{13}(u + v) \circ \check R_{23}(v) \,.$$

This spectral form (6) is close to the historical origin of Yang-Baxter equation, whence some authors refer to this form by default as the “the Yang-Baxter equation” (cf. Jimbo 1989 (2.1)).

Classical YBE

(…)

Variants

Beware that the term Yang-Baxter equation can mean (or be interpreted in the context of) any of several related but different concepts:

Yang-Baxter equations

• classical Yang-Baxter equation

• quantum Yang-Baxter equation

• dynamical quantum Yang-Baxter equation

• associative Yang-Baxter equation

• infinitesimal braid relation

• set theoretic Yang-Baxter equation

• quasitriangular bialgebra

References

for more see at quantum YBE, classical YBE, etc.

The (quantum) Yang-Baxter equation was named (cf. Perk & Au-Yang 2006) by Ludwig Fadeev in the late 1970s, in honor of:

• Chen Ning Yang: Some Exact Results for the Many-Body Problem in one Dimension with Repulsive Delta-Function Interaction, Phys. Rev. Lett. 19 (1967) 1312 [doi:10.1103/PhysRevLett.19.1312]

• Chen Ning Yang: S Matrix for the One-Dimensional $N$-Body Problem with Repulsive or Attractive $\delta$-Function Interaction, Phys. Rev. 168 (1968) 1920 [doi:10.1103/PhysRev.168.1920]

and

• Rodney J. Baxter: Partition function of the Eight-Vertex lattice model, Annals of Physics 70 1 (1972) 193-228 [doi:10.1016/0003-4916(72)90335-1]

• Rodney J. Baxter: Solvable eight-vertex model on an arbitrary planar lattice, Philos. Trans. Royal Society A 289 1359 (1978) [doi:10.1098/rsta.1978.0062]

• Rodney Baxter: Exactly Solved Models in Statistical Mechanics, Academic Press (1982, 1984, 1989) [webpage, pdf]

  (who spoke instead of the “star-triangle relation”).

Reviews:

• Michio Jimbo: Introduction to the Yang-Baxter Equation, International Journal of Modern Physics A 4 15 (1989) 3717-3757 [doi:10.1142/S0217751X89001497]

  reprinted in: Braid Group, Knot Theory and Statistical Mechanics, Advanced Series in Mathematical Physics 9, World Scientific (1991) [doi:10.1142/0796]

• Jacques H. H. Perk, Helen Au-Yang: Yang-Baxter Equations, Encyclopedia of Mathematical Physics 5 (2006) 465-473 [arXiv:math-ph/0606053]

Literature collection with focus on application to integrable systems:

• Michio Jimbo (ed.): Yang-Baxter Equation in Integrable Systems, Advanced Series in Mathematical Physics 10, World Scientific (1990) [doi:10.1142/1021]

See also:

• Wikipedia, Yang-Baxter equation

• eom, Yang-Baxter equation