nLab crossed homomorphism

Idea

In group theory, and specifically in group cohomology-theory, the notion of crossed homomorphisms (Def. below) is a generalization of that of group homomorphisms where a group action – of the domain-group $G$ by automorphisms on the codomain group $\Gamma$ – is incorporated.

Crossed homomorphisms are equivalently homomorphic sections of the projection to $G$ out of the corresponding semidirect product group $\Gamma \rtimes G$ (Prop. below).

This largely explains their relevance in all contexts of $G$-equivariant algebraic topology and equivariant differential topology, such as in equivariant principal bundle-theory (Prop. below) where semidirect product groups appear as $G$-equivariant groups.

In particular (Prop. below, which is not made explicit in traditional literature):

• the local coefficient bundle for non-abelian group cohomology in degree-1 is the image of the projection out of the semidirect product group under forming delooping groupoids,

• the strict (2,1)-category-theoretic sections of this bundle form precisely the groupoids of crossed homomorphisms with “crossed conjugations” (Def. below) between them;

• and the connected components of these groupoids is the non-abelian group cohomology $H^1(G,\Gamma)$ (Rem. , ).

This last fact is widely appreciated (see Rem. below) in the special case that $\Gamma$ is an abelian group, where it serves to define ordinary group cohomology with coefficients in degree 1.

Beware that, while the notion of crossed homomorphisms makes sense for group objects internal to any ambient category $\mathcal{C}$, it may not need to strictly coincide with that of cocycles in first group cohomology beyond $\mathcal{C} =$ Set (for reasons discussed at Lie group cohomology, or, for the case of profinite groups, in NSW 2008, p. 24).

Definition

In all of the following, let $G \,\in\,$ Grp be a group (or group object internal to an ambient category with finite products) and let $\Gamma \,\in\, G Act$ be an $G$-equivariant group, hence a group equipped with a group action

$$\alpha \;\colon\; G \xrightarrow{\;\;} Aut_{Grp}(\Gamma)$$

of $G$ on $\Gamma$ by group automorphisms, hence equivalently a semidirect product group, to be denoted:

$$1 \to \Gamma \xhookrightarrow{\;i\;} \Gamma \rtimes_\alpha G \xrightarrow{ \;pr_2\; } G \to 1 \,.$$

Component definition

Definition

A crossed homomorphism from $G$ to $\Gamma$ is a function (morphism in the ambient category)

$$\phi \;\colon\; G \xrightarrow{\;} \Gamma$$

satisfying the following “$G$-crossed” homomorphism property:

$$\underset{g_1, g_2 \in G}{\forall} \;\;\; \phi(g_1 \cdot g_2) \;=\; \phi(g_1) \cdot \alpha(g_1)\big( \phi(g_2) \big) \,.$$

Remark

Def. appears, already with the non-abelian generality in mind, back in Whitehead 1949, (3.1) (together with the notion of crossed modules, both as tools for analyzing homotopy types with non-trivial fundamental group). For abelian $\Gamma$ the definition is in Eilenberg & MacLane (1947) §3.1, MacLane (1975) IV (2.1) and many following references on group cohomology, e.g. Brown 1982, p. 45. For general non-abelian $\Gamma$ the notion is later used in Murayama & Shimakawa 1995 for discussion of equivariant principal bundles. In the context of nonabelian group cohomology it is reviewed in Gille & Szamuely, 2006, (1) on p. 25. Another textbook account is in Milne 2017, 15.a (16.a) in the pdf, aimed at application to algebraic groups.

Example

For $\alpha$ the trivial action, the notion of a crossed homomorphism (Def. ) reduces to that of an ordinary group homomorphism.

Remark

(as 1-cocycles in group cohomology)
In the special case that $\Gamma$ in Def. is an abelian group, crossed homomorphisms are also known as cocycles in group cohomology in degree 1 (e.g. Brown 1982, p. 45). In general they may be understood as 1-cocycles in non-abelian group cohomology (e.g. NSW 2008, p. 16).

Example

The constant function $const_{\mathrm{e}} \,\colon\, G \to \Gamma$ on the neutral element $\mathrm{e} \in \Gamma$ is always a crossed homomorphism (Def. ), being the trivial cocycle under the interpretation of Rem. .

Proposition

(as splittings/homomorphic sections of the semidirect product group-projection)
Crossed homomorphisms $G \to \Gamma$ (Def. ) are equivalently homomorphic sections of the projection out of the semidirect product group $\Gamma \rtimes_\alpha G \xrightarrow{pr_2} G$ (see also at split group extensions):

$$CrsHom(G,\,\Gamma) \;\simeq\; GrpHom_{{}_{/G}} \big( G ,\, \Gamma \rtimes_\alpha G \big) \;\coloneqq\; GrpHom(G, \, \Gamma \rtimes_\alpha G) \underset{ GrpHom(G,\,G) }{\times} \{id\} \,.$$

(e.g. Brown 1982, p. 88, NSW 2008, Ex. 1 on p. 24, Milne 2017, Ex. 15.1 (16.1 in the pdf))

Proof

By immediate unwinding of the definition of the semidirect product group, such a section is an assignment

$$\array{ G &\xrightarrow{\;}& \Gamma \rtimes_\alpha G \\ g &\mapsto& \big( \phi(g), \, g \big) }$$

such that

$$\underset{ g_1, g_2 \in G }{\forall} \;\;\;\;\; \big( \phi(g_1 \cdot g_2), \, g_1 \cdot g_2 \big) \;\overset{!}{=}\; \big( \phi(g_1), g_1 \big) \cdot \big( \phi(g_2), g_2 \big) \;=\; \Big( \phi(g_1) \cdot \alpha(g_1)\big(\phi(g_2)\big) ,\, g_1 \cdot g_2 \Big) \,.$$

Proposition

(graphs of crossed homomorphisms)
The graph of a function of a crossed homomorphism (Def. ) is a subgroup of the semidirect product group

(1)$$\widehat G \;\subset\; \Gamma \rtimes G \,, \;\;\;\; \text{such that} \;\;\;\; \mathrm{pr}_2\big(\widehat G\big) \simeq G \;\;\; \text{and} \;\;\; \widehat{G} \cap i(\Gamma) \;=\; \big\{ (\mathrm{e},\,\mathrm{e}) \big\} \,,$$

and every subgroup of this form arises as the graph of a unique crossed homomorphism.

This is, essentially, considered in tom Dieck 1969, Sec. 2.1, also Guillou, May & Merling 2017, Lem. 4.5.

Proof

The first statement is immediate from the definition.

For the converse, consider a subgroup $\widehat{G}$ as in (1). Then the subgroup property implies that

$$(\gamma,g), (\gamma',g) \,\in\, \widehat{G} \;\;\;\;\; \Rightarrow \;\;\;\;\; (\gamma' ,\, g) \cdot (\gamma ,\, g)^{-1} \;=\; (\gamma' ,\, g) \cdot \big( \alpha(g^{-1})(\gamma^{-1}) ,\, g^{-1} \big) \;=\; \big( \gamma' \cdot \gamma^{-1} ,\, \mathrm{e} \big) \;\;\; \in \; \widehat{G} \,.$$

From this the second condition in (1) implies that

$$(\gamma,\,g) ,\, (\gamma',\, g) \;\in\; \widehat{G} \;\;\;\; \Rightarrow \;\;\;\; \gamma = \gamma' \,.$$

Together with the first condition in (1) this implies that $\widehat{G}$ is the graph of a function $\phi \;\colon\; G \to \Gamma$. From this the claim follows by Prop. .

Remark

Subgroups of the form (1) are considered throughout articles by Peter May on equivariant principal bundles (e.g. in Lashof & May 1986, Thm. 10, May 1990, Thm. 7). That these are equivalently (graphs of) crossed homomorphisms may have been one the key observations that lead to Murayama & Shimakawa 1995, though the statement of Prop. was still not explicit there.

Definition

(crossed conjugation)
Two crossed homomorphisms $\phi_1, \phi_2$ (Def. ) are adjoint $\phi_1 \xrightarrow{\;\gamma\;} \phi_2$ if in their incarnation as homomorphisms to $\Gamma \rtimes G$ (Prop. ) they are related by conjugation with an element
$\gamma \in \Gamma \xhookrightarrow{\;} \Gamma \rtimes G$, in that:

(2)$$\underset{ g \in G }{\forall} \;\;\;\; \phi_2(g) \;=\; \gamma^{-1} \cdot \phi_1(g) \cdot \alpha(g)(\gamma) \,.$$

(e.g. Gille & Szamuely 2006, (2) on p. 25, Guillou, May & Merling 2017, Def. 4.11)

Remark

(as 1-coboundaries in group cohomology)
When $\Gamma$ is an abelian group, the conjugates according to Def. of the constant function $const_{0}$ (Exp. ) are of the form

(3)$$g \;\mapsto\; \alpha(g)(\gamma) - \gamma$$

(writing now in additive notation as befits an abelian group).

These (3) are also known as “principal crossed homomorphisms”.

With crossed homomorphisms understood as 1-cocycles in group cohomology (Rem. ), these elements (3) are the 1-coboundaries.

The definitions here apply verbatim also for non-abelian $\Gamma$, where we get non-abelian group cohomology (e.g. NSW 2008, p. 16).

As sliced functors of delooping groupoids

All the formulas above may conceptually be understood as follows:

Proposition

(groupoid of crossed homomorphisms is sliced functor groupoid of delooping groupoids)
The groupoid

(4)$$CrsHom(G,\Gamma) \sslash_{\!\! ad} \Gamma \;\; \coloneqq \big( CrsHom(G,\Gamma) \times \Gamma \rightrightarrows \Gamma \big) \;\; \;\;\; \in \; Grpd$$

of crossed homomorphisms (Def. ) with conjugations between them (Def. ) is isomorphic to the sliced functor groupoid of sections of the delooping groupoid $\mathbf{B}(\Gamma \rtimes G)$ of the semidirect product group:

(5)$$CrsHom(G,\Gamma) \sslash_{\!\! ad} \Gamma \;\; \simeq \;\; Fnctr_{{}_{/\mathbf{B}G}} \big( \mathbf{B}G ,\, \mathbf{B}(\Gamma \rtimes G) \big) \;=\; Fnctr \big( \mathbf{B}G ,\, \mathbf{B}(\Gamma \rtimes G) \big) \underset{ Fnctr \big( \mathbf{B}G ,\, \mathbf{B}G \big) }{\times} \{id\} \,.$$

We take this statement and the following proof from SS21.

Proof

By definition, a morphism in the groupoid on the right is a commuting diagram of functors and natural transformations as shown on the left of the following:

from SS21

Unwinding the definitions, it is clear that functors fitting into this diagram (indicated by the dashed single arrows on the left) are bijective (under passage to their component functions shown on the right) to group homomorphisms $G \to \Gamma \rtimes G$ whose composition with $\Gamma \rtimes G \xrightarrow{pr_2} G$ is the identity morphisms – hence are bijective to crossed homomorphisms, by Prop. .

Moreover, natural transformations $F \Rightarrow F'$ fitting into this diagram (indicated by the dashed double arrow on the left) must be such that their whiskering with $\mathbf{B}pr_2$ is the identity natural transformation, which means that their single component (as shown on the right) is of the form

$$\eta(\bullet) \;=\; \big( \gamma, \mathrm{e}\big) \;\;\; \in \; \Gamma \rtimes G \,,$$

where $\mathrm{e} \in G$ denotes the neutral element.

In conclusion, the naturality square in $\mathbf{B}(\Gamma \rtimes G)$ that all these components must make commute is of the form

$$\array{ \bullet &\;\;\;\;\mapsto\;\;\;\;& \bullet &\xrightarrow{\;\;\;\;\;\;(\gamma,\mathrm{e})\;\;\;\;\;\;}& \bullet \\ {}^{\mathllap{ g }} \big\downarrow && \big\downarrow {}^{\mathrlap{ \big( \phi_1(g),\, g\big) }} && \big\downarrow {}^{\mathrlap{ \big( \phi_2(g),\, g\big) }} \\ \bullet &\;\;\;\;\mapsto\;\;\;\;& \bullet &\xrightarrow{\;\;\;\;\;\;(\gamma,\mathrm{e})\;\;\;\;\;\;}& \bullet } {\phantom{AAAAAAAAAAA}} \in \; \mathbf{B}(\Gamma \rtimes G) \,.$$

Since composition in the delooping groupoid is given by the group product, this is equivalently the condition that

(6)$$\big( \phi_2(g) ,\, g \big) \;=\; \big( \gamma^{-1} ,\, \mathrm{e} \big) \cdot \big( \phi_1(g) ,\, g \big) \cdot \big( \gamma ,\, \mathrm{e} \big) \;\;\;\;\; \in \; \Gamma \rtimes G \,,$$

which is evidently equivalent to the defining relation from Def. .

Remark

(conjugacy classes of crossed homomorphisms are non-abelian first group cohomology)
In view of the identification of crossed homomorphisms with 1-cocycles in non-abelian group cohomology, we may identify their conjugacy classes (Def. ), hence, by Prop. , the connected components of the sliced functor groupoid (5) with the group cohomology sets (at least for discrete groups):

$$CrsHom(H,\Gamma)_{/\sim} \;\simeq\; \pi_0 \Big( Fnctr_{{}_{/\mathbf{B}G}} \big( \mathbf{B}G ,\, \mathbf{B}(\Gamma \rtimes G) \big) \Big) \;\simeq\; H^1_{Grp}(G,\Gamma) \,.$$

But we also get higher homotopy information, beyond the cohomology set:

Proposition

(automorphism group of crossed homomorphisms)
For $\phi \colon G \xrightarrow{\;} \Gamma$ a crossed homomorphism (Def. ), its automorphism group in the conjugation groupoid (4), hence the subgroup

$$Aut(\phi) \;\coloneqq\; Aut_{{}_{ CrsHom(G,\Gamma) \sslash_{\! ad} \Gamma }} \big( \phi \big) \;=\; \Big\{ \, \gamma \,\in\, \Gamma \,\vert\, \phi(-) \,=\, \gamma^{-1} \cdot \phi(-) \cdot \alpha(-)(\gamma) \, \Big\} \;\;\; \subset \; \Gamma$$

of crossed conugations (Def. ) that fix it, is, equivalently, the intersection of $i(\Gamma) = \{ (\gamma, \mathrm{e}) \,\vert\, \gamma \in \Gamma \}$ with

1. the centralizer $C_{{}_{\Gamma \rtimes G}}\big(Graph(\phi)\big)$

2. the normalizer $N_{{}_{\Gamma \rtimes G}}\big(Graph(\phi)\big)$

of the graph of $\phi$ inside the semidirect product group:

$$\begin{aligned} Aut(\phi) & \;\;=\;\; i(\Gamma) \,\cap\, C_{{}_{\Gamma \rtimes G}}\big(Graph(\phi)\big) \\ & \;\;=\;\; i(\Gamma) \,\cap\, N_{{}_{\Gamma \rtimes G}}\big(Graph(\phi)\big) \,. \end{aligned}$$

(compare Lashof & May 1986, below Thms. 10, 11)

Proof

The first statement is immediate from the re-formulation (6) of crossed conjugation (2).

From this, the second statement follows by observing that the action in the form (6) manifestly fixes the $G$-component under projection along $pr_2$, while the graph of a function $G \to \Gamma$ has at most one element with a given $G$-component.

Properties

Restriction to subgroups

Proposition

(Weyl group acts on non-abelian group 1-cohomology of subgroup)
For $H \subset G$ a subgroup, the set of crossed homomorphisms $H \to \Gamma$ (Def. ), with respect to the restricted action of $H$ on $\Gamma$, carries a group action of the normalizer subgroup $N_G(H) \,\subset\, G$, given by

(7)$$\array{ N_G(H) \times CrsHom(H,\,G) &\xrightarrow{\;\;}& CrsHom(H,\,G) \\ (n, \phi) &\mapsto& \phi_{n} \mathrlap{ \;\coloneqq\; \alpha(n) \Big( \phi \big( n^{-1} \cdot (-) \cdot n \big) \Big) \,. } }$$

Moreover, on crossed-conjugation classes (Def. ), hence on first non-abelian group cohomology, this action descends to an action of the Weyl group $W_G(H) \coloneqq N_G(H)/H$:

$$H^1_{Grp}(H,\,\Gamma) \;\;\; \in \; W_G(H) Act(Sets) \,.$$

Proof

1. Action property. It is clear that (7) is a group action if only $\phi_n$ is indeed a crossed homomorphism. This follows by a direct computation:

$$\begin{array}{lll} \phi_n( h_1 \cdot h_2 ) & \;=\; \alpha(n) \Big( \phi \big( n^{-1} \cdot h_1 \cdot h_2 \cdot n \big) \Big) & \text{definition of}\; \phi_n \\ & \;=\; \alpha(n) \Big( \phi \big( n^{-1} \cdot h_1 \cdot n \cdot n^{-1} \cdot h_2 \cdot n \big) \Big) & \text{group property of}\; N_G(H) \subset G \\ & \;=\; \alpha(n) \Big( \phi \big( n^{-1} \cdot h_1 \cdot n \big) \cdot \alpha(n^{-1} \cdot h_1 \cdot n) \big( \phi( n^{-1} \cdot h_2 \cdot n ) \big) \Big) & \text{crossed homomorphism property of} \; \phi \\ & \;=\; \alpha(n) \Big( \phi \big( n^{-1} \cdot h_1 \cdot n \big) \Big) \cdot \alpha(h_1 \cdot n) \Big( \phi\big( n^{-1} \cdot h_2 \cdot n \big) \Big) & \text{action property of} \; \alpha \\ & \;=\; \alpha(n) \Big( \phi \big( n^{-1} \cdot h_1 \cdot n \big) \Big) \cdot \alpha(h_1) \bigg( \alpha(n) \Big( \phi\big( n^{-1} \cdot h_2 \cdot n \big) \Big) \bigg) & \text{action property of} \; \alpha \\ & \;=\; \phi_n(h_1) \cdot \alpha(h_1) \big( \phi_n(h_2) \big) & \text{definition of}\; \phi_n \mathrlap{\,.} \end{array}$$

2. Descent to crossed-conjugation classes. To see that the action (7) descends to group cohomology, we need to show for

$$\phi'(-) \;=\; \gamma^{-1} \cdot \phi(-) \cdot \alpha(-)(\gamma)$$

a crossed conjugation between some $\phi'$ and $\phi$, that there also exists a crossed conjugation between $\phi'_n$ and $\phi_n$. The following direct computation shows that this is given by crossed conjugation with $\alpha(n)(\gamma)$:

$$\begin{array}{lll} \phi'_n(h) & \;=\; \alpha(n) \Big( \gamma^{-1} \cdot \phi\big( n^{-1} \cdot h \cdot n \big) \cdot \alpha \big( n^{-1} \cdot h \cdot n \big) (\gamma) \Big) & \text{assumption with definition of} \; \phi_n \\ & \;=\; \alpha(n) \big( \gamma^{-1} \big) \cdot \alpha(n) \Big( \phi\big( n^{-1} \cdot h \cdot n \big) \Big) \cdot \alpha(h) \Big( \alpha(n)(\gamma) \Big) & \text{action property of} \; \alpha \\ & \;=\; \big( \alpha(n)(\gamma) \big)^{-1} \cdot \phi_n(h) \cdot \alpha(h) \big( \phi(n)(\gamma) \big) & \text{definition of} \; \phi_n \,. \end{array}$$

Alternative argument for 1. & 2. Alternatively, the previous two statements also follow more immediately, by using the identification from Prop. of the conjugation groupoid of crossed homomorphisms $\phi \colon H \to \Gamma$ with that of homomorphic sections $\big( \phi(-),\, (-) \big) \,\colon\, H \to \Gamma \rtimes H$. In this latter incarnation, the action by $n$ is simply the “conjugation action by the adjoint action”, in that:

$$n \;\colon\; \big( \phi(-),\, (-) \big) \;\; \mapsto \;\; \big( \phi_n(-),\, (-) \big) \;\; = \;\; \big( \mathrm{e} ,\, n \big) \cdot \Big( \phi \big( n^{-1}\cdot(-)\cdot n \big) ,\, \big( n^{-1} \cdot(-) \cdot n \big) \Big) \cdot \big( \mathrm{e} ,\, n^{-1} \big) \,.$$

In this formulation it is manifest that homomorphisms and conjugation are preserved, and the only point to check is that the section-property is also respected, which is immediate.

3. Descent to action of Weyl group. To conclude, we need to show that the action of $H \subset B_G(H)$ is trivial on conjugacy classes, hence that for $n \in H \subset N(H)$ there is a crossed conjugation between $\phi_n$ and $\phi$. The following direct computation shows that this is given by crossed conjugation with $\phi(n)$ (which is well-defined, by the assumption that $n \in H$):

$$\begin{array}{lll} \phi_n(h) & \;=\; \alpha(n) \Big( \phi \big( n^{-1} \cdot h \cdot n \big) \Big) & \text{definition of} \; \phi_n \\ & \;=\; \alpha(n) \bigg( \phi(n^{-1}) \cdot \alpha(n^{-1}) \Big( \phi(h) \cdot \alpha(h) \big( \phi(n) \big) \Big) \bigg) & \text{crossed homomorphism property of} \; \phi \\ & \;=\; \alpha(n) \big( \phi(n^{-1}) \big) \cdot \phi(h) \cdot \alpha(h) \big( \phi(n) \big) & \text{action property of} \; \alpha \\ & \;=\; \big( \phi(n) \big)^{-1} \cdot \phi(h) \cdot \alpha(h) \big( \phi(n) \big) & \text{crossed homomorphism property of} \; \phi \mathrlap{\,.} \end{array}$$

Examples

In relation to crossed modules

Example

(a relation to crossed modules)
Let $(\Gamma \xrightarrow{\delta} G)$ be a crossed module, with the corresponding strict 2-group

$$\mathcal{G} \;\coloneqq\; \big( \Gamma \rtimes G \underoverset { (\delta(-))\cdot(-) } {pr_2} {\rightrightarrows} G \big) \,.$$

Then in the strict (2,1)-category of strict 2-groups, the 2-morphisms out of the identity 1-morphism on $\mathcal{G}$ are in bijection to the crossed homomorphisms $G \to \Gamma$:

(8)$$CrsHom(G,\Gamma) \;\simeq\; \big\{ id_{\mathcal{G}} \Rightarrow F \,\vert\, F \in Str2Grp(\mathcal{G}, \mathcal{G}) \big\} \,.$$

Namely, such a 2-morphism is a natural transformation $\eta \colon id_{\mathcal{G}} \Rightarrow F$ of endofunctors of the underlying action groupoid, whose component function

$$\eta_0 \,\colon\, Obj(\mathcal{G}) \xrightarrow{\;} Mor(\mathcal{G})$$

is a group homomorphism

$$\eta_0 \,\colon\, G \xrightarrow{\;} \Gamma \rtimes G$$

such that

$$s \big( \eta_0(g) \big) \;=\; (id_{\mathcal{G}})_0(g) \;=\; g \,,$$

where

$$s \,\coloneqq\, pr_2 \;\colon\; \Gamma \times G \xrightarrow{\;} G$$

is the source map of the groupoid $\mathcal{G}$.

This means that the admissible $\eta_0$ are precisely the homomorphic sections of $\Gamma \rtimes G \xrightarrow{\;} G$. Conversely, by the invertiblity of all morphisms involved, every such $\eta_0$ is the component homomorphism of some 2-morphism $\eta$ out of $id_{\mathcal{G}}$.

Therefore the statement (8) follows by Prop. .

The analogous statement for general 2-morphisms is indicated in Noohi 07, p. 12.

In relation to equivariant bundles

Let $G \,\in\, Grp(Top)$ and $\Gamma \,\in\, Grp\big( G Act(Top) \big)$ be topological groups which are compact Lie groups (to be on the safe side). Then:

Proposition

(equivariant connected components of equivariant classifying spaces)
A G-equivariant classifying space $B_G \Gamma$ for $G$-equivariant $\Gamma$-principal bundles exists, and the connected components of its $H$-fixed loci, for compact subgroups $H \subset G$, are in bijection to the conjugacy classes (Def. ) of crossed homomorphisms (Def. ) from $H$ to $\Gamma$ (with respect to the restricted action of $H$ on $\Gamma$):

(9)$$\pi_0 \left( \left( B_G \Gamma \right)^{H} \right) \;\; \simeq \;\; CrsHom(H,\Gamma)_{/\sim} \,.$$

Proof

After a little reformulation via Prop. and Prop. , this is the statement of Lashof & May 1986, Thm. 10, May 1990, Thm. 7.

In view of the explicit construction of universal equivariant principal bundles in Murayama & Shimakawa 1995, one may understand the statement of Prop. on elementary grounds, as follows:

Consider the following $G$-action objects internal to Groupoids:

• the delooping groupoid

  $$\mathbf{B}\Gamma \,\coloneqq\, \big( \Gamma \rightrightarrows \ast\big) \;\;\; \in \; G Act\big( Groupids \big)$$

  via the $G$-action on $\Gamma$ by group automorphisms;

• the pair groupoid

  $$\mathbf{E}G \,\coloneqq\, \big( G \times G \rightrightarrows G\big)$$

  via the left multiplication action of $G$ on all three copies of $G$;

• the functor groupoid

  (10)$$Fnctr \big( \mathbf{E}G ,\, \mathbf{B}\Gamma \big) \;\;\; \in \; G Act\big( Groupids \big)$$

  with the induced conjugation action on component functions of functors and natural transformations:

  $$g \,\colon\, F(-) \,\mapsto\, g \cdot F\big( g^{-1}\cdot (-) \big) \,.$$

Proposition

(crossed homomorphisms are fixed loci in functor groupoid from $\mathbf{E}G$ to $\mathbf{B}\Gamma$)
If $G$ a discrete group, then for each subgroup $H \subset G$, there is an equivalence of groupoids (in fact of topological groupoids)

$$Fnctr \big( \mathbf{E}G ,\, \mathbf{B}\Gamma \big)^H \;\simeq\; CrsHom(H,\Gamma) \sslash_{\!\!ad} \Gamma$$

between

• the $H$-fixed sub-groupoid of the functor groupoid (10) and

• the conjugation groupoid (4) of crossed homomorphisms $H \to \Gamma$.

This is essentially the statement of Guillou, May & Merling 2017, Thm. 4.14, Cor. 4.15. We take the following detailed proof from SS21. Its ingredients are needed below in the proof of Prop. .

Proof

By Prop. the statement is equivalently that

$$Fnctr \big( \mathbf{E}G ,\, \mathbf{B}G \big)^H \;\simeq\; Fnctr_{{}_{/\mathbf{B}H}} \big( \mathbf{B}H ,\, \mathbf{B}(\Gamma \rtimes H) \big) \,.$$

In the special case $H = G$ there is in fact an isomorphism, evidently exhibited by the following functor:

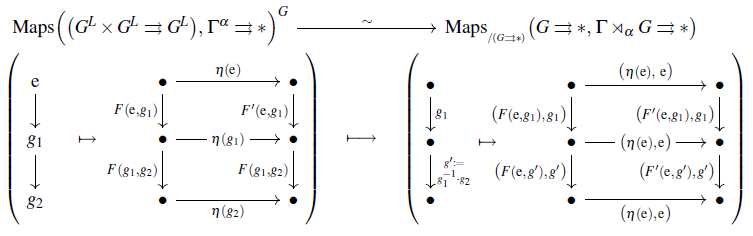
For general $H \subset G$, choose a section of the coset space-projection

(11)$$\sigma \,\colon\, G/H \xrightarrow{\;} G \,, \;\;\;\; \text{such that} \; \sigma([\mathrm{e}]) \,=\, \mathrm{e} \,,$$

which exists and is continuous by the assumption that $G$ is discrete.

Observe that then $\mathbf{E}G$ is generated, under

1. composition,

2. taking inverses,

3. acting with elements of $H$

by the following two classes of morphisms:

(12)$$\big\{ (\mathrm{e} \to h) \,\vert\, h \in H \big\} \,, \;\;\; \big\{ \mathrm{e} \to \sigma([g]) \,\vert\, [g] \in G/H \big\} \;\;\;\;\; \subset \; G \times G \,.$$

Using this, consider the following expression for a pair of comparison functors:

Here

• $L$ is the restriction along $(H \times H \rightrightarrows H) \xhookrightarrow{\;} (G \times G \rightrightarrows G)$ of the previous isomorphism for $H =$G;

• $R$ is given in terms of the above generating morphisms (12) as follows:

(13)$$\;\;$$

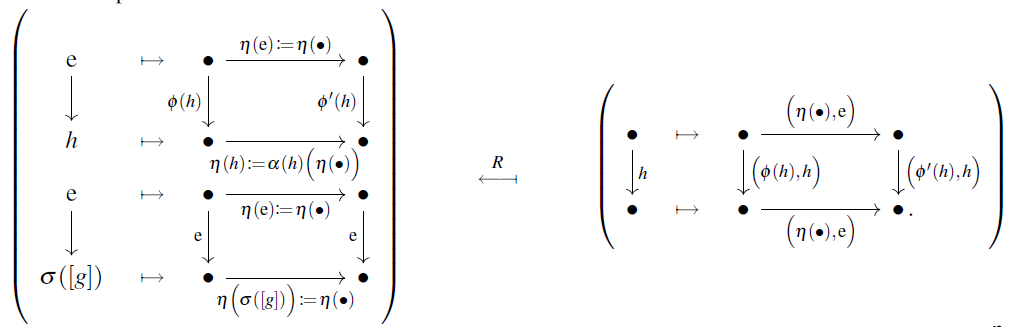
One readily sees that this is well-defined, and that $L \circ R \,=\, id$.

Therefore it is now sufficient to give a natural transformation $id \xRightarrow{\eta} R \circ L$, hence for each functor $F$ a natural transformation

$$\eta_F \,\colon\, F \Rightarrow R \circ L(F) \,.$$

This may be taken as follows, again stated in terms of the generating morphisms (12):

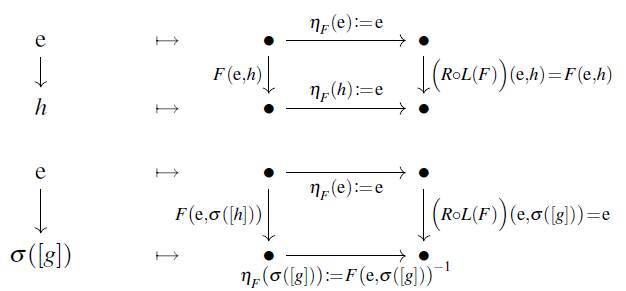
It just remains to check that this is indeed natural in the functors $F$, which amounts, for each $H$-equivariant natural transformation $G \xRightarrow{\beta} F'$, to the commutativity of the two types of squares shown on the right here:

Indeed, the top square commutes by the $H$-equivariance of $\beta$, while the bottom square commutes by the naturality of $\beta$.

Proposition

(residual Weyl group-action on fixed locus of equivariant classifying space)
Transported through the equivalence of Prop. , the canonical group action (see this Prop.) of the Weyl group $W_G(H)$ on the $H$-fixed locus $Fnctr\big(\mathbf{E}G ,\, \mathbf{B}\Gamma\big)^H$ becomes, on connected components $\pi_0 \big( CrsHom(H,\,\Gamma) \sslash_{\!\!ad} \Gamma \big) \;\; \simeq \;\; H^1_{Grp}(H,\,\Gamma)$, the $W_G(H)$-action on the non-abelian group 1-cohomology of $H$ from Prop. .

We take this statement and the following proof from SS21.

Proof

We make explicit use of the functors $L, R$ constructed in the proof of Prop. . Noticing that $R$ is a section of $L$, we need to (1) send a crossed homomorphism up with $R$, (2) there act on it with $n$, (3) send the result back with $L$. The result is the desired induced action.

Explicitly, by the definition of $L$ in the proof of Prop. , this way a crossed homomorpism $\phi \,\colon\, H \to \Gamma$ is sent by $n \in N_G(H)$ to the assignment

(14)$$h \,\mapsto\, \Big(L\big( n \cdot (R \phi) \big)\Big)(h) \;=\; \alpha(n) \Big( (R\phi) \big( n^{-1} ,\, n^{-1} \cdot h \big) \Big) \,.$$

It just remains to evaluate the right hand side.

Notice that the definition of $L$ is independent of the choice of $\sigma \,\colon\, G/H \xrightarrow{\;} G$ (11), and that $R$ (whose definition does depend on this choice ) is a section for each choice. Hence we may choose $\sigma$ in a way convenient way for any given $n$.

Now if $n \in H \subset N_G(H)$ then its canonical action on the $H$-fixed locus is trivial, and also the claimed induced action is trivial, so that in this case there is nothing further to be proven. Therefore we assume now that $n$ is not in $H$, and then we choose $\sigma$ such as to pick $n^{-1}$ as the representative in its $H$-coset:

$$\sigma\big( \big[n^{-1}\big] \big) \;\coloneqq\; n^{-1} \,.$$

Notice that with this choice, $R\phi$ (13) assigns the neutral element to the morphism between the neutral element and $n^{-1}$ in the pair groupoid:

(15)$$(R\phi)\big(\mathrm{e}, n^{-1}\big) \;=\; \mathrm{e} \,, \;\;\;\; (R\phi)\big(n^{-1}, \mathrm{e}\big) \;=\; \mathrm{e} \;\;\;\;\; \,.$$

This way, the right hand side of (14) is evaluated as follows:

$$\begin{array}{lll} \Big(L\big( n \cdot (R \phi) \big)\Big)(h) & \;=\; \alpha(n) \Big( (R\phi) \big( n^{-1} ,\, n^{-1} \cdot h \big) \Big) & \text{by}\;\text{(14)} \\ & \;=\; \alpha(n) \big( (R\phi)(\mathrm{e},\, n^{-1} \cdot h) \big) & \text{by}\;\text{(15)} \\ & \;=\; \alpha\big(n^{-1} \cdot h \cdot n \cdot n\big) \big( (R\phi)(n^{-1} \cdot h^{-1} \cdot n,\, n^{-1}) \big) & \text{by} \; H\text{-equivariance of} \; R\phi \\ & \;=\; \alpha\big(n^{-1} \cdot h \cdot n \cdot n\big) \big( (R\phi)(n^{-1} \cdot h^{-1} \cdot n,\, \mathrm{e}) \big) & \text{by}\;\text{(15)} \\ & \;=\; \alpha(n) \big( (R\phi)(\mathrm{e},\, n^{-1} \cdot h \cdot n) \big) & \text{by} \; H\text{-equivariance of} \; R\phi \\ & \;=\; \alpha(n) \big( \phi(n^{-1} \cdot h \cdot n) \big) & \text{by definition of} \; R \; \text{(13)} \mathrlap{\,.} \end{array}$$

This is indeed the claimed formula (7).

Related concepts

• group extension

• group cohomology

• semidirect product group

• Fox derivative

Literature

To abelian groups

Discussion for the special case that $\Gamma$ is an abelian group:

in the context of homological algebra:

• Saunders Mac Lane, Section IV.2 of: Homology (1975) reprinted as Classics in Mathematics. Springer-Verlag, Berlin, 1995. x+422 pp. ISBN 3-540-58662-8 (doi:10.1007/978-3-642-62029-4)

in the context of group cohomology:

• Samuel Eilenberg, Saunders MacLane, §3.1 in: Cohomology Theory in Abstract Groups. I, Annals of Mathematics, Second Series 48 1 (1947) 51-78 [doi:10.2307/1969215]

• Kenneth Brown, p. 45 of: Cohomology of Groups, Graduate Texts in Mathematics, 87, Springer 1982 (doi:10.1007/978-1-4684-9327-6)

To general groups

The general non-abelian notion:

In discussion of homotopy theory (together with crossed modules):

• J. H. C. Whitehead, Section 3 of: Combinatorial Homotopy II, Bull. Amer. Math. Soc., 55, (1949), 453 – 496 (euclid:1183513797)

A brief textbook account in this generality

• Jürgen Neukirch, Alexander Schmidt, Kay Wingberg, pages 16 & 24 in: Cohomology of Number Fields, Springer Grundlehren der mathematischen Wissenschaften 323, Springer 2008 (doi:10.1007/978-3-540-37889-1, webpage)

As 1-cocycles in non-abelian group cohomology:

• Philippe Gille, Tamás Szamuely, Def. 2.3.2 in: Central Simple Algebras and Galois Cohomology, Cambridge University Press 2006 (doi:10.1017/CBO9780511607219, pdf)

• James Milne, Sec. 15.a-b & 3.k (16.a-b & 27.a in the pdf) of: Algebraic Groups, Cambridge University Press 2017 (doi:10.1017/9781316711736, webpage, pdf)

• Groupprops, First cohomology set with coefficients in a non-abelian group

In view of homotopy fixed points:

• R. Virk, Section 3 of: On fixed point stacks (arXiv:2112.06871)

In discussion of equivariant principal bundles:

• Tammo tom Dieck, Sec. 2.1 in: Faserbündel mit Gruppenoperation, Arch. Math 20, 136–143 (1969) (doi:10.1007/BF01899003)

  (not using the terminology “crossed homomorphism”, but already characterizing their graphs, as in Lem. )

• Mitutaka Murayama, Kazuhisa Shimakawa, p. 2 of: Universal equivariant bundles, Proc. Amer. Math. Soc. 123 (1995), 1289-1295 (doi:10.1090/S0002-9939-1995-1231040-9)

• Bertrand Guillou, Peter May, Mona Merling, around Def. 4.1 in: Categorical models for equivariant classifying spaces, Algebr. Geom. Topol. 17 (2017) 2565-2602 (arXiv:1201.5178, doi:10.2140/agt.2017.17.2565)

Discussion for finite groups:

• Tsunenobu Asai, Yugen Takegahara, On the number of crossed homomorphisms, Hokkaido Math. J. 28 3 (1999) 535-543 (doi:10.14492/hokmj/1351001235)

Discussion for Lie groups:

• Karl-Hermann Neeb, Def. 2.3 in: Lie group extensions associated to projective modules of continuous inverse algebras, Archivum Mathematicum, 44 5 (2008) 465-489 (dml:127115)

Discussion in relation to crossed modules:

• Behrang Noohi, Notes on 2-groupoids, 2-groups and crossed-modules, Homotopy, Homology, and Applications, 9, (2007), no. 1, 75–106 (arXiv:math/0512106)