nLab
topological G-space

Idea

In the context of topology, a topological $G$-space (traditionally just $G$-space, for short, if the context is clear) is a topological space equipped with an action of a topological group $G$ – the equivariance group (usually taken to be the topological group underlying a compact Lie group, such as a finite group).

The canonical homomorphisms of topological $G$-spaces are $G$-equivariant continuous functions, and the canonical choice of homotopies between these are $G$-equivariant continuous homotopies (for trivial $G$-action on the interval).

A $G$-equivariant version of the Whitehead theorem says that on G-CW complexes these $G$-equivariant homotopy equivalences are equivalently those maps that induce weak homotopy equivalences on all fixed point spaces for all subgroups of $G$ (compact subgroups, if $G$ is allowed to be a Lie group).

By Elmendorf's theorem, this, in turn, is equivalent to the (∞,1)-presheaves over the orbit category of $G$. See below at In topological spaces – Homotopy theory.

See (Henriques-Gepner 07) for expression in terms of topological groupoids/orbispaces.

In the context of stable homotopy theory the stabilization of $G$-spaces is given by spectra with G-action; these lead to equivariant stable homotopy theory. See there for more details. (But beware that in this context one considers the richer concept of G-spectra, which have a forgetful functor to spectra with G-action but better homotopy theoretic properties. ) The union of this as $G$ is allowed to vary is the global equivariant stable homotopy theory.

Properties

Change of equivariance groups

We discuss how any homomorphism of topological groups induces an adjoint triple of functors between the corresponding $Topological G Spaces$ (e.g. May 96, Sec. I.1, DHLPS 19, p.8, see also at induced representation for a formulation in homotopy type theory)

Throughout, let $G_1, G_2 \in$ TopologicalGroups and consider a continuous homomorphism of topological groups

(1)$$\phi \;\colon\; G_1 \longrightarrow G_2 \,.$$

Pullback action

Definition

(pullback action)
Given a topological group homomorphism $\phi$ (1), write

$$Topological G_1 Spaces \overset{ \;\;\; \phi^\ast \;\;\; }{\longleftarrow} Topological G_2 Spaces$$

for the functor which takes a topological G2-space $(X,\rho)$ to the same underlying topological space $\rho$, equipped with the $G_1$-action $\rho(\phi(-))$.

Example

(restricted action)

For $\phi \coloneqq i \colon H \hookrightarrow G$ a subgroup-inclusion, the pullback action in Def. is obtained by restricting the $G$-action to that of its subgroup $H$.

Induced action

Definition

(induced action)
Given a topological group homomorphism $\phi$ (1), the induced action functor

$$Topological G_1 Actions \overset{ G_2 \times_{G_1} (-) }{\longrightarrow} Topological G_2 Actions$$

sends $X \in Topological G_1 Spaces$ to the quotient space of its Cartesian product with $G_2$ by the diagonal action of $G_1$ (which on $G_2$ is by inverse right multiplication through $\phi$):

$$G_2 \times_{G_1} X \;\coloneqq\; \big( G_2 \times X \big) \big/ \big( (g_2, x) \sim (g_2 \cdot \phi(g_1)^{-1}, g_1 \cdot x) \,\vert\, g_1 \in G_1 \big)$$

and equipped with the $G_2$-action given by left multiplication on the $G_2$-factor.

Example

(Quotients as induced actions)

If $\phi \coloneqq G \longrightarrow 1$ is the terminal morphims to the trivial group, then its induced action (Def. ) is the operation of forming $G$-quotient spaces (the $G$-orbit-space):

$$\array{ Topological G Actions &\longrightarrow& Topological 1 Actions \mathrlap{ \; = TopologicalSpaces } \\ X &\mapsto & 1 \times_G X \mathrmlap{ \; = X/G } \,. }$$

Proposition

(induced action is left adjoint to pullback action)
Given a topological group homomorphism $\phi$ (1), the induced action functor (Def. ) is left adjoint to the pullback action functor (Def. ):

$$G_1 Spaces \underoverset {\underset{\phi^\ast}{\longleftarrow}} {\overset{G_2 \times_{G_1} (-)}{\longrightarrow}} {\;\;\; \bot \;\;\; } G_2 Spaces \,.$$

Proof

For $X$ a $G_1$-space and $Y$ a $G_2$-space, consider a $G_2$-equivariant function out of the induced action

$$G_2 \times_{G_1} X \overset{\;\;\; f \;\;\;}{\longrightarrow} Y \,.$$

Since the $G_2$-orbit of

$$X = G_1 \times_{G_1} X \hookrightarrow G_2 \times_{G_1} X$$

is the entire domain space on the left, by $G_2$ equivariance, this function is completely determined by its restriction along this inclusion to a $G_1$-equivariant function $\tilde f \;\colon\; X \to Y$, hence to a homomorphism $\tilde f \;\colon\; X \to \phi^\ast Y$. This correspondence

$$f \leftrightarrow \tilde f$$

is clearly a natural bijection and hence establishes the hom-isomorphisms characterizing the adjunction.

Coinduced action

Definition

(coinduced action)

Given a topological group homomorphism $\phi$ (1), the coinduced action functor

$$Topological G_1 Actions \overset{ Maps(G_2,-)^{G_1} }{\longrightarrow} Topological G_2 Actions$$

sends $X \in Topological G_1 Spaces$ to the $G_1$-fixed locus in the mapping space between topological spaces equipped with $G_1$-actions (on $G_2$ the $\phi$-induced left multiplication action) and itself equipped with the $G_2$-action given by

(2)$$\array{ G_2 \times Maps(G_2,X)^{G_1} & \overset{}{\longrightarrow} & Maps(G_2,X)^{G_1} \\ (g_2, h) &\mapsto& h\big( (-) \cdot g_2 \big) \,. }$$

Example

(Fixed loci as coinduced actions)

Let $H \subset G$ be a topological subgroup and consider the group homomorphism (1) to be the $H$-quotient group coprojection from the normal subgroup $N(H) \subset G$:

$$\phi \coloneqq q \;\colon\; N(H) \longrightarrow N(H)/H \,.$$

Then for any $N(H)$-space $X$ (which in practice will usually be a $G$-space after restriction of its action along $N(H) \hookrightarrow G$, Example ) we have that its coinduced action (Def. ) is its $H$-fixed locus $X^H$ equipped with its residual $N(H)$-action:

$$Maps \big( N(H)/H, X \big)^{N(H)} \;\; \simeq \;\; X^H \,.$$

Proposition

(coinduced action is right adjoint to pullback action)

Given a topological group homomorphism $\phi$ (1), the pullback action functor (Def. ) is the left adjoint and the coinduced action functor (Def. ) is the right adjoint in a pair of adjoint functors

$$G_1 Spaces \underoverset { \underset{ Maps \big( G_2, - \big)^{G_1} }{\longrightarrow} } { \overset{ \phi^\ast }{ \longleftarrow } } {\bot} G_2 Spaces$$

Proof

To see the defining hom-isomorphism, consider a $G_1$-equivariant continuous function

$$\phi^\ast X \overset{ \;\;\; f \;\;\; }{ \longrightarrow } Y \,.$$

From this we obtain the following function

$$\array{ X & \overset{ \tilde f }{ \longrightarrow } & Maps \big( G_2, Y \big)^{G_1} \\ x &\mapsto& \big( g_2 \mapsto f( g_2 \cdot x ) \big) \,, }$$

where $e \in G_2$ denotes the neutral element.

This is manifestly:

• well-defined, due to the $G_1$-equivariance of $f$;

• continuous, being built from composition of continuous map;

• $G_2$-equivariant with respect to the action (2).

Conversely, given a $G_2$-equivariant continuous function $X \overset{\tilde f}{\longrightarrow} Maps\big(G_2, Y\big)^{G_1}$, we obtain the following function

$$\array{ \phi^\ast X &\overset{}{\longrightarrow}& Y \\ x &\mapsto& \tilde f(x)(e) \,. }$$

This is:

• continuous, being the composition of continuous functions;

• $G_1$-equivariant due to the equivariance properties of $\tilde f$:

  $$\begin{aligned} \phi(g_1) \cdot x & \mapsto \tilde f \big( \phi(g_1)\cdot x \big) (e) \\ & = \tilde f ( x ) \big( e \cdot \phi(g_1) \big) \\ & = \tilde f ( x ) \big( \phi(g_1) \cdot e \big) \\ & = g_1 \cdot \big( \tilde f ( x ) ( e ) \big) \end{aligned}$$

Finally, it is clear that these transformations $f \leftrightarrow \tilde f$ are natural, hence it only remains to see that they are bijective:

Plugging in the above constructions we find indeed:

$$\widetilde {\tilde f} \;\colon\; x \mapsto f(e \cdot x) = f(x)$$

and

$$\widetilde {\widetilde {\tilde f}} \;\colon\; x \mapsto \big( g_2 \mapsto \underset{ {= \tilde f(x)(e \cdot g_2)} \atop {= \tilde f(x)(g_2)} }{ \underbrace{ \tilde f(g_2\cdot x)(e) } } \big) \,.$$

Remark

For the analogous statement of cofree-actions of simplicial groups on simplicial sets see at Borel model structure this Prop..

Fixed loci with residual Weyl group action

Combining these change-of-equivariance grouo adjunctions (from above) to “pull-push” through the correspondence

we obtain the fixed locus-functor in the form in which it appears in Elmendorf's theorem, namely with the residual Weyl group-action on the fixed loci:

Example

(Fixed loci with residual Weyl-group action as coinduced action)

Let $H \subset G$ be a subgroup-inclusion. Write

• $N(H) \hookrightarrow G$ for the corresponding normalizer subgroup inclusion

• $N(H) \twoheadrightarrow N(H)/H = W(H)$ for the coprojection to its quotient group by $H$ (the “Weyl group” of $H$).

Then the composite of

1. forming the pullback action (Def. ) along $N(H) \hookrightarrow G$ (the restricted action, Example )

2. forming the coinduced action (Def. ) along $N(H) \twoheadrightarrow N(H)/H$ (the passage to fixed loci, Example )

is the passage to the $H$-fixed locus $(-)^H$ equipped with its residual Weyl group-action, and Prop. with Prop. shows that this construction is a right adjoint:

Further limits and colimits

Lemma

(recognition of cartesian quotient projections) Let $G$ be a compact topological group and let $f \colon X \longrightarrow Y$ be morphism of Hausdorff $G$-spaces.

Then its quotient naturality square

(3)$$\array{ X &\overset{f}{\longrightarrow}& Y \\ \big\downarrow && \big\downarrow \\ X/G &\overset{f/G}{\longrightarrow}& Y/G }$$

is a pullback square if and only if $f$ preserves isotropy groups, i.e. if and only if for each $x \in X$ we have

$$G_x \,\simeq\, G_{f(x)}$$

as an isomorphism of stabilizer subgroups of $G$.

(Bykov-Flores 15, Prop. 4.1)

Remark

The assumption in Lemma is met in particular when the action on both sides is free, whence all isotropy groups are trivial.

This is the case in which $X$ and $Y$ are $G$-principal bundles without, however, necessarily needing to be locally trivial for Lemma to apply (“Cartan principal bundles”).

On the other hand, even if $G$ is not compact but $X \to X/G$ and $Y \to Y/G$ are $G$-principal bundles which are locally trivial, then it follows again that (3) is a pullback (since then the universal comparison morphism $X \to Y \times_{X/G} Y/G$ is a morphism of locally trivial principal bundles over the common base space $X/G$, which is an isomorphism since it is so on any open cover over which both $X$ and $Y \times_{X/G} Y/G$ trivialize).

Equivariant Tietze extension theorem

See at equivariant Tietze extension theorem

Model structure and homotopy theory

The standard homotopy theory on $G$-spaces used in equivariant homotopy theory considers weak equivalences which are weak homotopy equivalence on all (ordinary) fixed loci for all suitable subgroups. This is presented by the fine model structure on topological G-spaces, which, byElmendorf's theorem, is equivalent to (∞,1)-presheaves over the orbit category of $G$.

On the other hand there is also the standard homotopy theory of infinity-actions, presented by the Borel model structure, in this context also called the “coarse” or “naive” equivariant model structure (Guillou).

Examples

We discuss some classes of examples of G-spaces.

Euclidean $G$-spaces

Let $V \in RO(G)$ be an orthogonal linear representation of a finite group $G$ on a real vector space $V$. Then the underlying Euclidean space $\mathbb{R}^V$ inherits the structure of a G-space

We may call this the Euclidean G-space associated with the linear representation $V$.

Representation spheres

Let $V \in RO(G)$ be an orthogonal linear representation of a finite group $G$ on a real vector space $V$. Then the one-point compactification of the underlying Euclidean space $\mathbb{R}^V$ inherits the structure of a G-space with the point at infinity a fixed point. This is called the $V$-representation sphere

Representation tori

Let $V \in RO(G)$ be an orthogonal linear representation of a finite group $G$ on a real vector space $V$.

If $G$ is the point group of a crystallographic group inside the Euclidean group

$$N \rtimes G \hookrightarrow Iso(\mathbb{R}^V)$$

then the $G$-action on the Euclidean space $\mathbb{R}^V$ descends to the quotient by the action of the translational normal subgroup lattice $N$ (this Prop.). The resulting $G$-space is an n-torus with $G$-action, which might be called the representation torus of $V$

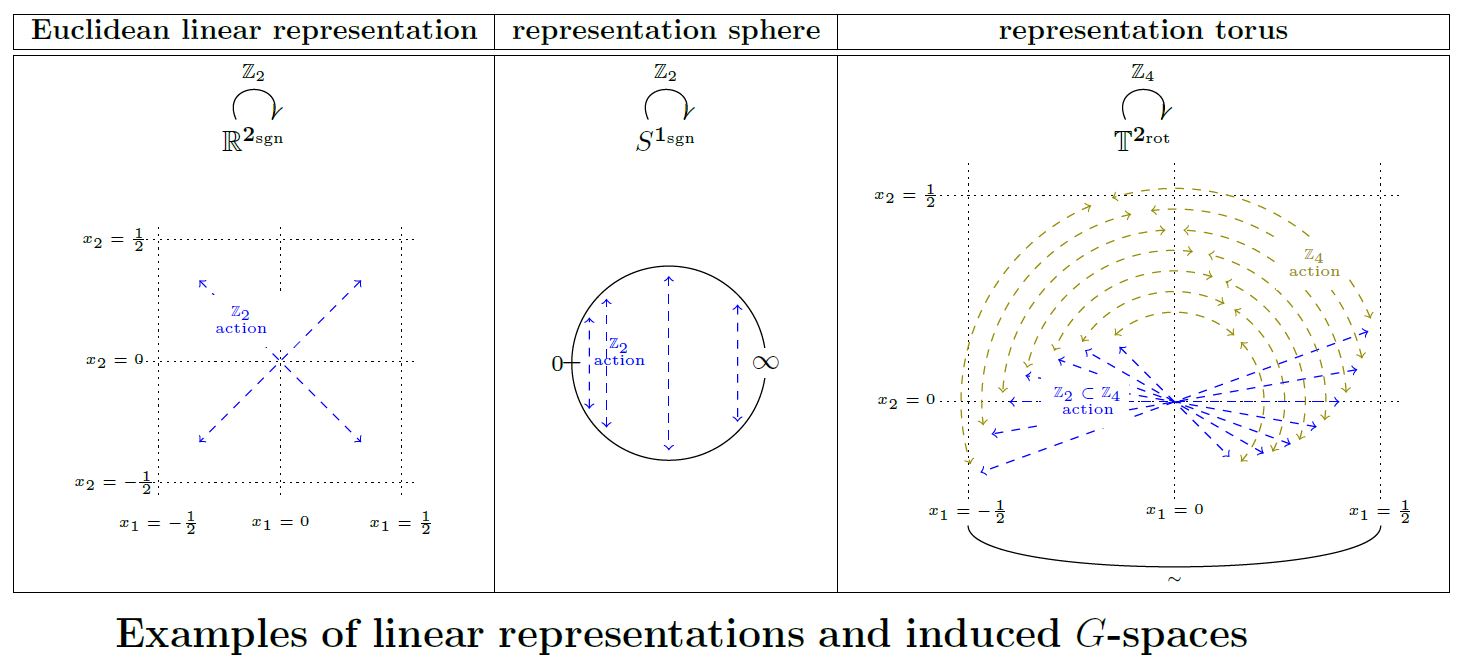
graphics grabbed from SS 19

Projective $G$-space

Let $G$ be a finite group (or maybe a compact Lie group) and let $V$ be a $G$-linear representation over some topological ground field $k$.

Then the corresponding projective G-space is the quotient space of the complement of the origin in (the Euclidean space underlying) $V$ by the given action of the group of units of $k$ (from the $k$-vector space-structure on $V$):

$$k P(V) \;:=\; \big( V \setminus \{0\} \big) / k^\times$$

and equipped with the residual $G$-action on $V$ (which passes to the quotient space since it commutes with the $k$-action, by linearity).

G-CW complexes

See at G-CW complex.

Related concepts

• G-set, G-manifold, simplicial group action

• fixed point space

• slice theorem

• equivariant bundle

• cyclotomic space

Rezk-global equivariant homotopy theory:

cohesive (∞,1)-topos	its (∞,1)-site	base (∞,1)-topos	its (∞,1)-site
global equivariant homotopy theory $PSh_\infty(Glo)$	global equivariant indexing category $Glo$	∞Grpd $\simeq PSh_\infty(\ast)$	point
… sliced over terminal orbispace: $PSh_\infty(Glo)_{/\mathcal{N}}$	$Glo_{/\mathcal{N}}$	orbispaces $PSh_\infty(Orb)$	global orbit category
… sliced over $\mathbf{B}G$: $PSh_\infty(Glo)_{/\mathbf{B}G}$	$Glo_{/\mathbf{B}G}$	$G$-equivariant homotopy theory of G-spaces $L_{we} G Top \simeq PSh_\infty(Orb_G)$	$G$-orbit category $Orb_{/\mathbf{B}G} = Orb_G$

See also

• rational topological G-space

• equivariant rational homotopy theory

  vector G-space

• equivariant stable homotopy theory

• equivariant rational stable homotopy theory

References

(For basics see also the references at group actions.)

Early appearance of the notion (as “transformation groups”):

• Felix Klein, Vergleichende Betrachtungen über neuere geometrische Forschungen (1872) Mathematische Annalen volume 43, pages 63–100 1893 (doi:10.1007/BF01446615)

  English translation by M. W. Haskell:

  A comparative review of recent researches in geometry, Bull. New York Math. Soc. 2, (1892-1893), 215-249. (euclid:1183407629 retyped pdf)

See also:

• Jean-Louis Koszul, Lectures on Groups of Transformations, Tata Institute 1965 (pdf, pdf)

Textbook accounts:

• Richard Palais, The classification of $G$-spaces, Memoirs of the AMS 36, 1960 (ISBN:978-0-8218-9979-3 pdf, pdf)

  (the term “G-space” appears here)

• Glen Bredon, Introduction to compact transformation groups, Academic Press 1972 (ISBN 9780080873596, pdf)

• Tammo tom Dieck, Chapter 8 in: Transformation Groups and Representation Theory, Lecture Notes in Mathematics 766, Springer 1979 (doi:10.1007/BFb0085965)

• Tammo tom Dieck, Transformation Groups, de Gruyter 1987 (doi:10.1515/9783110858372)

• Peter May et al., Section I.1 of: Equivariant homotopy and cohomology theory, CBMS Regional Conference Series in Mathematics, vol. 91, Published for the Conference Board of the Mathematical Sciences, Washington, DC, 1996 (ISBN: 978-0-8218-0319-6 pdf, pdf)

• Alejandro Adem, James Davis, Topics in Transformation Groups, Chapter 1 in: Handbook of Geometric Topology, 2001, Pages 1-54 (doi:10.1016/B978-044482432-5/50002-0, pdf)

More discussion in the context of equivariant homotopy theory:

• Bert Guillou, A short note on models for equivariant homotopy theory (pdf, pdf)

• André Henriques, David Gepner, Homotopy Theory of Orbispaces (arXiv:math/0701916)

• Alexander Bykov, Raúl Juárez Flores G-fibrations and twisted products, Topology and its Applications Volume 196, Part B, December 2015, Pages 379-397 (doi:10.1016/j.topol.2015.05.011)

Specifically in the context of proper equivariant homotopy theory:

• Dieter Degrijse, Markus Hausmann, Wolfgang Lück, Irakli Patchkoria, Stefan Schwede, Proper equivariant stable homotopy theory, Memoirs of the AMS (arXiv:1908.00779)

See also the references at equivariant homotopy theory.

The special case of smooth Lie group-actions on smooth manifolds:

Lecture notes:

• Eckhard Meinrenken, Group actions on manifolds, Lecture Notes 2003 (pdf, pdf)