nLab S5 modal logic

Idea

In modal logic the moniker “S5” refers to the logic obtained from S4 modal logic by adjoining the axiom scheme that there is the implication

$$\lozenge p \to \Box \lozenge p \,.$$

In the possible worlds semantics for modal logic, S5 corresponds precisely to those Kripke frames $\big(W \colon Set, \, R \colon W \times W \to Prop\big)$ where the relation $R$ is an equivalence relation [Kripke (1959) (1964), cf. Fagin, Halpern, Moses & Vardi (1995) Thm. 3.1.5 (c)].

Via dependent type theory

In mild generalization of the discussion at necessity & possibility – Via dependent types, we may observe that the modal operators in S5 Kripke semantics

(Here we are writing — following notation for subtypes — $P \,\colon\,W \to Prop$ for a $W$-dependent proposition, equivalently a proposition about the elements of $W$, equivalently the subset of $W$ where the proposition holds.)

are precisely those arising as adjoint pairs of (co)monads induced on the left from a base change adjoint triple (the categorical semantics in Set of dependent pair type $\dashv$ context extension $\dashv$ dependent function type-formation) along display maps $W \to \Gamma \equiv W_{/R}$ identified with the quotient coprojection of the Kripke frame:

(Obvious as this may be, the only existing reflection of this fact in the literature may be a side remark in Awodey 2006, p. 279, albeit not relating to dependent type formation.)

Remark

This suggests that one may equivalently regard dependent type theory as a universal form of epistemic modal type theory, in generalization of how modal logics may be viewed as just another perspective on (fragments of) first-order logic (as in Blackburn, van Benthem & Wolter (2007) pp. xiii): In both cases one switches perspective from type formation by base change adjoint triples (of quantification or dependent (co)product formation, respectively) to the induced adjoint pair of (co)monads. (Another example of a change in perspective of this form occurs when describing descent as monadic descent).

Remark

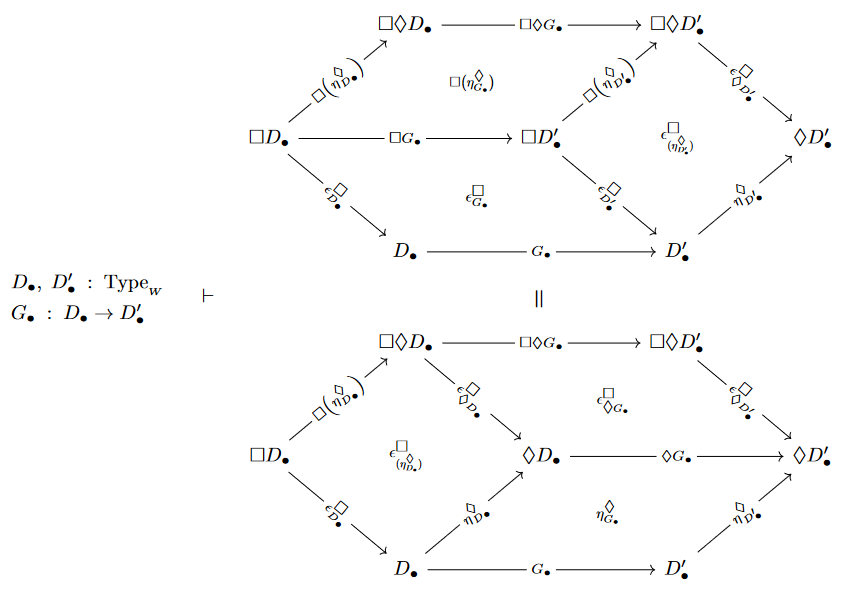
The above (co)monadic formulation of modal logic makes manifest another basic point not usually discussed in the subject, namely that the canonical epistemic entailments

are natural transformations.

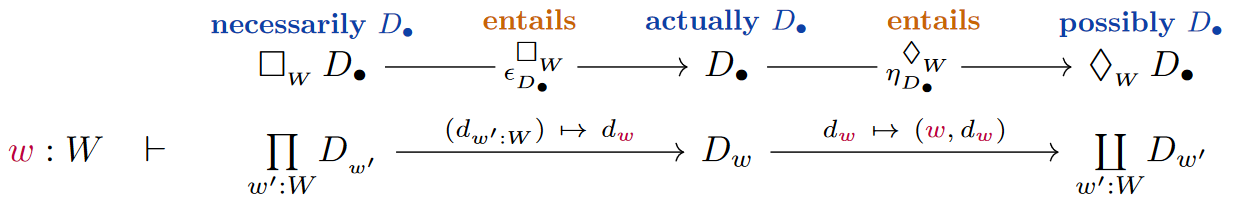
This means that the following squares commute. Their pasting to the hexagonal commuting diagram as shown may not have received attention (?):

Related concepts

type of modal logic	relation in its Kripke frames
K modal logic	any relation
K4 modal logic?	transitive relation
T modal logic	reflexive relation
B modal logic?	symmetric relation
S4 modal logic	reflexive & transitive relation
S5 modal logic	equivalence relation

(following BdRV (2001) Table 4.1; cf. Fagin, Halpern, Moses & Vardi (1995) Thm. 3.1.5)

• modal logic, S4 modal logic

• epistemic modal logic, necessity and possibility

• K modal logic

• T modal logic

• Kripke frame

• Löb's axiom

References

General

The terminology “S5” in modal logic originates with:

• Clarence I. Lewis, Cooper H. Langford, App. II, p 501 of: Symbolic Logic (1932), Dover (2000) [App. II pdf]

The geometric model for S5 modal logic via Kripke frames originates with:

• Saul A. Kripke, A Completeness Theorem in Modal Logic, The Journal of Symbolic Logic 24 1 (1959) 1-14 [doi:10.2307/2964568, jstor:2964568, pdf]

• Saul A. Kripke, Semantical Analysis of Modal Logic I. Normal Modal Propositional Calculi, Mathematical Logic Quaterly 9 5-6 (1963) 67-96 [doi:10.1002/malq.19630090502]

See also:

• Wikipedia, S5 (modal logic)

A natural deduction-formulation and making explicit the modal operator as a comonad:

• Gavin M. Bierman, Valeria de Paiva, Intuitionistic necessity revisited, School of Computer Science research reports-University of Birmingham CSR (1996) [researchgate, pdf]

• Gavin M. Bierman, Valeria de Paiva, On an Intuitionistic Modal Logic Studia Logica 65 (2000) 383–416 [doi:10.1023/A:1005291931660, pdf]

• Satoshi Kobayashi, Monad as modality, Theoretical Computer Science 175 1 (1997) 29-74 [doi:10.1016/S0304-3975(96)00169-7]

• Natasha Alechina, Michael Mendler, Valeria de Paiva, Eike Ritter: Categorical and Kripke Semantics for Constructive S4 Modal Logic, in Computer Science Logic. CSL 2001 Lecture Notes in Computer Science 2142, Springer (2001) 292 [doi:10.1007/3-540-44802-0_21]

Understanding of S5 Kripke semantics as base change along the lines discussed at necessity and possibility – via dependent types:

• Steve Awodey, p. 279 in: Category theory, Oxford University Press (2006, 2010) [doi:10.1093/acprof:oso/9780198568612.001.0001, ISBN:9780199237180, pdf]

S5 modal logic as epistemic logic

Discussion of S5 modal logic as epistemic logic:

• Robert J. Aumann, Interactive epistemology I: Knowledge, International Journal of Game Theory 28 (1999) 263–300 $[$doi:10.1007/s001820050111$]$

$[$Ditmarsch, Hoek & Kooi (2008):$]$ “in Aumann’s survey paper on interactive epistemology the reader will immediately recognise the system S5.”

• Joseph Y. Halpern, Yoram Moses, §2.3 in: A guide to completeness and complexity for modal logics of knowledge and belief, Artificial Intelligence 54 3 (1992) 319-379 $[$doi:10.1016/0004-3702(92)90049-4$]$

• Ronald Fagin, Joseph Y. Halpern, Yoram Moses, Moshe Y. Vardi, Reasoning About Knowledge, The MIT Press (1995) $[$ISBN:9780262562003$]$

p. 35: “in a precise sense the S5 properties completely characterize our definition of knowledge”

• Joseph Y. Halpern, Should knowledge entail belief?, Journal of Philosophical Logic 25 5 (1996) 483-494 $[$jstor:30226583, philpapers:HALSKE$]$

• Melvin Fitting, Logics of Knowlege, Sec. 9 in: Modal proof theory, Ch. 2 in: The Handbook of Modal Logic, Studies in Logic and Practical Reasoning 3 (2007) 85-183 $[$doi:10.1016/S1570-2464(07)80005-X, book webpage$]$

pp. 121: “What standard logics of knowledge capture is not actual knowledge, but potential knowledge — what one is entitled to know. The switch to potential knowledge means we drop all considerations of complexity $[...]$ It is easy to see that, under such an assumption, a knowledge modality should be a normal modal operator. But, what else should be required? $[...]$ All these together make a knowledge operator obey the S5 conditions.”

• Wiebe van der Hoek, Marc Pauly, Epistemic Logic, Sec 4 in: Modal logic for games and information, Ch. 20 in: The Handbook of Modal Logic, Studies in Logic and Practical Reasoning 3 (2007) 85-183 $[$doi:10.1016/S1570-2464(07)80023-1, book webpage$]$

p. 198: “Modal epistemic logic, the logic of knowledge, provides a very natural interpretation to the accessibility relation in Kripke models. For an agent $i$, two worlds $w$ and $v$ are connected (written $R_i w v$), if the agent cannot (epistemically) distinguish them. In other words, we have $R_i v w$ if, according to $i$’s information at $w$, the world might as well be in state $v$, or that $v$ is compatible with i’s information at w. Using this interpretation of access, $R_i$ is obviously an equivalence relation. $[...]$ Thus, we are in the realm of the multi-modal logic $S5_m$.”

• Hans Ditmarsch, Wiebe Hoek, Barteld Kooi, Epistemic Logic, chapter 2 in: Dynamic Epistemic Logic, Studies In Epistemology, Logic, Methodology, And Philosophy Of Science (SYLI) 337, Springer (2008) $[$doi:10.1007/978-1-4020-5839-4_2, pdf$]$

p. 11: “The logical system S5 is by far the most popular and accepted epistemic logic”

• Dov Samet, S5 knowledge without partitions, Synthese 172 (2010) 145–155 $[$doi:10.1007/s11229-009-9469-0$]$

• Meghyn Bienvenu, Hélène Fargier, Pierre Marquis, Knowledge Compilation in the Modal Logic S5, Proceedings of the AAAI Conference on Artificial Intelligence 24 1 (2010) $[$doi:10.1609/aaai.v24i1.7587, pdf$]$

  p. 1: “Propositional epistemic logic S5 is a well-known modal logic which is suitable for representing and reasoning about the knowledge of a single agent”

• Rasmus Rendsvig, John Symons, Epistemic Logic, The Stanford Encyclopedia of Philosophy (2011) $[$web$]$

“Fagin, Halpern, Moses, and Vardi (1995) and many others use S5 for knowledge”

• Rachel Boddy, Epistemic Issues and Group Knowledge, Amsterdam (2014) $[$pdf$]$

p. 13: “Formal approaches to epistemology – such as game theory and computer science – typically assume the S5 conditions for knowledge, which is (partly) explained by the convenient formal properties of the logic. Philosophers typically opt for a weaker notion. Hintikka (1962), for instance, argues that the proper logic for knowledge is the modal system S4”

• Yakoub Salhi and Michael Sioutis, A Resolution Method for Modal Logic S5, EPiC Series in Computer Science 36 (2015) 252–262 $[$pdf$]$

• Ronald de Haan, Iris van de Pol, On the Computational Complexity of Model Checking for Dynamic Epistemic Logic with S5 Models $[$arXiv:1805.09880$]$