nLab quantum logic
Context
Type theory
natural deduction metalanguage, practical foundations
type theory (dependent, intensional, observational type theory, homotopy type theory)
computational trinitarianism =
propositions as types +programs as proofs +relation type theory/category theory
Quantum systems
-
quantum algorithms:
Contents
Idea
Broadly speaking, quantum logic is meant to be a kind of formal logic that is to traditional formal logic as quantum mechanics is to classical mechanics: a formal framework which is supposed to be able to express the statements whose semantics is the totality of all what is verifiable by measurement in a quantum system (quantum measurement).
In its traditional and default meaning due to (Birkhoff-vonNeumann 1936) “quantum logic” refers specifically to the orthocomplemented lattice of closed linear subspaces of a Hilbert space of quantum states. Later it was proposed (Yetter 90, Pratt 92, 93, Abramsky-Duncan 05, Girard 11) that a better way to think of the BvN quantum lattices is as the propositions in linear logic (Girard 87), the categorical logic of symmetric monoidal categories.
There is also the proposal (Heunen-Landsman-Spitters 07) that quantum logic should be understood as being the internal logic of Bohr toposes.
In quantum computing the quantum analog of classical logic gates are called quantum logic gates.
History and Critique
Typically in the literature the term “quantum logic” is taken to refer very specifically to the first proposal for such a formalization due to Birkhoff-von Neumann 1936. In this proposal, given a quantum mechanical system with a Hilbert space of states, the logical propositions about the system are taken to correspond to (the projections to) closed subspaces, with implication given by inclusion of such subspaces. Hence Birkhoff-von Neumann quantum logic is given by the lattice of closed linear subspaces of Hilbert spaces (regarded as a Hilbert lattice).
This formalization is often understood as being the default meaning of “quantum logic”. But the proposal has later been much criticised, for its lack of key properties that one would demand of any formal logic.
For instance in Abramsky & Coecke (2007) it is called a “non-logic”:
The term quantum logic is usually understood in connection with the 1936 Birkhoff-von Neumann proposal to consider the (closed) linear subspaces of a Hilbert space ordered by inclusion as the formal expression of the logical distinction between quantum and classical physics. While in classical logic we have deduction, the linear subspaces of a Hilbert space form a non-distributive lattice and hence there is no obvious notion of implication or deduction. Quantum logic was therefore always seen as logically very weak, or even as a non-logic. In addition, it has never given a satisfactory account of compound systems and entanglement.
Here by “no deduction” is meant “no deduction theorem”.
And for example in (Heunen-Landsman-Spitters 07, p. 4) it says the following:
Attractive and revolutionary as this spatial quantum “logic” may appear it faces severe problems. The main logical drawbacks are:
Due to its lack of distributivity, quantum ‘logic’ is difficult to interpret as a logical structure.
In particular, despite various proposals no satisfactory implication operator has been found (so that there is no deductive system in quantum logic).
Quantum ‘logic’ is a propositional language; no satisfactory generalization to predicate logic has been found.
Quantum logic is also problematic from a physical perspective. Since (by various theorems and wide agreement) quantum probabilities do not admit an ignorance interpretation, -valued truth values attributed to propositions by pure states via the Born rule cannot be regarded as sharp (i.e. {0, 1}-valued) truth values muddled by human ignorance. This implies that, if represents a quantum-mechanical proposition, it is wrong to say that either or its negation holds, but we just do not know which of these alternatives applies. However, in quantum logic one has the law of the excluded middle in the form for all . Thus the formalism of quantum logic does not match the probabilistic structure of quantum theory responsible for its empirical content.
But notice that one may argue that the first three points here are squarely resolved by thinking of BvN-quantum logic as embedded into linear logic, we come back to this in a moment. Concerning the last point one might argue that the propositions in BvN-quantum logic concern the quantum measurement-outcomes (only), for which, at least in some interpretations, it does make sense to speak of a definite result.
In Girard 2011, page xii it says:
Among the magisterial mistakes of logic, one will first mention quantum logic, whose ridiculousness can only be ascribed to a feeling of superiority of the language – and ideas, even bad, as soon as they take a written form – over the physical world. Quantum logic is indeed a sort of punishment inflicted on nature, guilty of not yielding to the prejudices of logicians… just like Xerxes had the Hellespont – which had destroyed a boat bridge – whipped.
For more and more objective criticism see Girard 2011, section 17.
Girard had introduced the class of formal logic systems called linear logic and it has been argued that linear logic and more generally linear type theory does faithfully capture the essence of quantum mechanics (Yetter 90. Pratt 92, Abramsky-Duncan 05, Duncan 06), see (Baez-Stay 09 for an introductory exposition). This is due to the fact that the categorical semantics of linear logic is in symmetric monoidal categories such as those used in the description of finite quantum mechanics in terms of dagger-compact categories. In particular the category of (finite dimensional) Hilbert spaces whose subobjects/propositions form the Birkhoff-von Neumann style quantum logic does interpret linear logic.
This is stated explicitly for instance in (Pratt 92, p.4):
These objections are overcome in the extension of quantum logic to linear logic as a dynamic quantum logic.
Notice that the subobjects in a category of (finite dimensional) Hilbert spaces, and hence the propositions in the categorical logic of Hilbert spaces, are the (closed) linear subspaces. Therefore Birkhoff-von Neumann quantum logic is indeed subsumed as a fragment of linear logic. This (obvious) fact was highlighted in Crown 1975 and then later with more of categorical logic in place and emphasizing dagger-structures in Heunen 2008, Harding 2008 Heunen-Jacobs 2009, Coecke-Heunen-Kissinger 2013. Also CCGP 09, section 9.3):
both orthologic (or weakenings thereof) and linear logic share the failure of lattice distributivity. In particular, the fragment of linear logic that includes just negation and the additive connectives is nothing but a version of the paraconsistent quantum logic PQL.
That seems to make much of the above-listed criticism appear in a different light. For instance there is also a natural notion of dependent linear type theory and that does yield a well-behaved kind of predicate logic with quantifiers for linear logic.
Approaches
Birkhoff-von Neumann quantum logic
The original proposal for quantum logic by Birkhoff & von Neumann 1936 (BvN quantum logic) is to regard, given a quantum system with Hilbert space of states , the Hilbert lattice of closed linear subspaces as the set of propositions about the quantum system.
Then:
-
logical conjunction is given by intersection of linear subspaces
-
logical disjunction is given by forming the linear span
of two linear subspaces.
-
logical negation is given by forming orthogonal complement:
Notice that quantum states in the conjunction may be linear combinations of states in and , in reflection of the superposition principle of quantum mechanics. As a result, the BvN disjunction does not distribute over conjunction, and hence the BvN lattice of quantum propositions is not a distributive lattice.
Tensor logic of Quantales
The tensor product of Hilbert spaces – which in the jargon of linear logic would be called the multiplicative conjunction – makes the above Hilbert lattice a quantale.
Linear logic and dependent linear type theory
We point out that — at least for the finite dimensional Hilbert spaces relevant in quantum information theory — BvN quantum logic is just the linear logic of a kind of linearly-dependent linear types inside dependent linear type theory interpreted in VectBund over the complex numbers.
(Notice that it is the linearity of linear logic, which enforces (see there for more) both the no-cloning theorem and the no-deleting theorem of quantum physics/quantum information theory.)
Namely, the linear types in VectBund form the subcategory FinDimVect. Any finite dimensional vector space admits a hermitian inner product making it a Hilbert space. For the discussion of logical conjunction and disjunction this Hilbert space structure plays no role and we may and will ignore it.
So given , a proposition about it in the internal logic sense of dependent type theory is, in categorical semantics, a (-1)-truncated object in the slice category over , hence a linear subspace
We need to consider the (co)fiber products of such objects (discussed here at FinDimVect):
Logical conjunction of such slice objects is given by their cartesian product in the slice, hence by the fiber product of their inclusion maps in . This is evidently given by the intersection of the subspaces:
Logical disjunction of such slice objects is given by the (-1)-truncation of their coproduct in the slice. Using that coproducts in slices are computed in the ambient category (see there) this is given by the image of the abstract direct sum of the subspaces, which is the linear span:
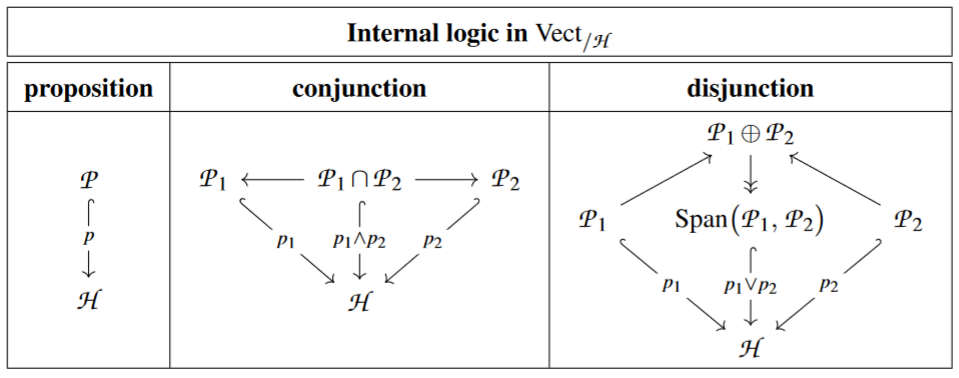
The historical debate above about justifying BvN logic as a formal logic is ultimately rooted in the fact that Vect is not a cartesian closed category (much less a locally cartesian closed category) so that its internal logic is exotic.
Bohr toposes
See at Bohr topos for more.
Related concepts
Literature
Original articles
The original proposal on quantum logic:
- Garrett Birkhoff, John von Neumann: The logic of quantum mechanics, Annals of Mathematics 37 823-843 (1936) [doi:10.2307/1968621]
Historical account of John von Neumann‘s further reasoning on quantum logic, which led him to develop the theory of von Neumann algebra factors:
- Miklos Rédei, Why John von Neumann did not Like the Hilbert Space formalism of quantum mechanics (and what he liked instead), Studies in History and Philosophy of Modern Physics 27 4 (1996) 493-510 [doi:10.1016/S1355-2198(96)00017-2]
Review:
-
Karl Svozil: Quantum Logic, Discrete Mathematics and Theoretical Computer Science, Springer (1998) [ISBN:9789814021074]
-
Karl Svozil: Quantum logic. A brief outline [arXiv:quant-ph/9902042]
Proposal for an enhancement of the Birkhoff-von Neumann axioms by probability measures:
- George Mackey, Section 2-2 of: The Mathematical Foundations of Quantum Mechanics: a Lecture-note Volume, Mathematical physics monograph series, Benjamin (1963), Dover (2004) [google books]
further discussed in:
-
Andrew Gleason, Measures on the closed subspaces of a Hilbert space, Journal of Mathematics and Mechanics, Indiana Univ. Math. J. 6 4 (1957), 885-893 [IUMJ:56050, pdf]
-
Samuel S. Holland Jr., Orthomodularity in infinite dimensions; a theorem of M. Solèr, Bull. Amer. Math. Soc. (N.S.) 32 (1995) 205-234 [arXiv:math.RA/9504224]
-
Pavlos Kazakopoulos, Georgios Regkas, Infinite Permutation Groups and the Origin of Quantum Mechanics [arXiv:2307.13044]
An account of quantum logic within a comprehensive discussion of quantum mechanics and its interpretation of quantum mechanics:
- Erhard Scheibe, pp 71 in: The logical analysis of quantum mechanics, Pergamon Press Oxford (1973)
Discussion of categorical logic in symmetric monoidal categories (not just of vector spaces but of vector bundles) and hence of linear logic as quantum logic:
- G. D. Crown, On some orthomodular posets of vector bundles, Journ. of Natural Sci. and Math. 15 1-2 (1975) 11-25
much later followed up in:
- John Harding, Taewon Yang, The Logic of Bundles, International Journal of Theoretical Physics 54 12 (2015) [doi:10.1007/s10773-015-2760-6]
The introduction of linear logic with the suggestion of a possible relation to quantum physics:
- Jean-Yves Girard, Linear logic, Theoretical Computer Science 50 1 (1987) [doi:10.1016/0304-3975(87)90045-4]
but remaining undecided:
Girard (1987), p. 7: “One of the wild hopes that this suggests is the possibility of a direct connection with quantum mechanics… but let’s not dream too much!”
The relation of linear logic to quantales, which have otherwise been proposed as providing a quantum logic:
- David Yetter, Quantales and (noncommutative) linear logic, Journal of Symbolic Logic 55 (1990) 41-64 [doi:10.2307/2274953]
Maybe the first to really say that linear logic is a good kind of quantum logic:
-
Vaughan Pratt, Linear logic for generalized quantum mechanics, in Proceedings of Workshop on Physics and Computation (PhysComp’92) (1992) 166-180 [doi:10.1109/PHYCMP.1992.615518, pdf, pdf]
-
Vaughan Pratt, The second calculus of binary relations, Mathematical Foundations of Computer Science 1993. MFCS 1993, Lecture Notes in Computer Science 711, Springer (1993) [doi:10.1007/3-540-57182-5_9]
“Linear logic is seen in its best light as the realization of the Curry-Howard isomorphism for linear algebra”
First practical development of this perspective (see quantum information theory in terms of dagger-compact categories):
-
Samson Abramsky, Bob Coecke, A categorical semantics of quantum protocols, Proceedings of the 19th IEEE conference on Logic in Computer Science (LiCS’04). IEEE Computer Science Press (2004) [arXiv:quant-ph/0402130, doi:10.1109/LICS.2004.1319636]
-
Samson Abramsky, Ross Duncan, A Categorical Quantum Logic, Mathematical Structures in Computer Science, Volume 16, Issue 3 (2006) pp. 469 - 489 (arXiv:quant-ph/0512114, doi:10.1017/S0960129506005275)
-
Ross Duncan, Types for quantum mechanics, 2006 (pdf, slides)
and as a paradigm for quantum programming languages (quantum lambda-calculus):
-
Benoît Valiron, A functional programming language for quantum computation with classical control, MSc thesis, University of Ottawa (2004) [doi:10.20381/ruor-18372, pdf]
-
Peter Selinger, Benoît Valiron, A lambda calculus for quantum computation with classical control, Proc. of TLCA 2005 [arXiv:cs/0404056, doi:10.1007/11417170_26]
-
Peter Selinger, Benoît Valiron, Quantum Lambda Calculus, in: Semantic Techniques in Quantum Computation, Cambridge University Press (2009) 135-172 [doi:10.1017/CBO9781139193313.005, pdf]
That therefore in particular categories of phase spaces and categories of cobordisms (the domains of functorial quantum field theory) interpret quantum logic qua linear logic has been highlighted in
-
John Baez, Quantum Quandaries: a Category-Theoretic Perspective, in D. Rickles et al. (ed.) The structural foundations of quantum gravity, Clarendon Press (2006) 240-265 [arXiv:quant-ph/0404040, ISBN:9780199269693]
-
Sergey Slavnov, From proof-nets to bordisms: the geometric meaning of multiplicative connectives, Mathematical Structures in Computer Science 15 06 (2005) 1151-1178 [doi:10.1017/S0960129505004974]
-
Sergey Slavnov, Geometrical semantics for linear logic (multiplicative fragment), Theoretical Computer Science 357 1-3 (2006) 215-229 [doi:10.1016/j.tcs.2006.03.020]
For more exposition along these lines see Baez & Stay (2009).
Interpreting the linear logic-sector of bunched logic as a quantum logic:
- Li Zhou, Gilles Barthe, Justin Hsu, Mingsheng Ying, Nengkun Yu, A Quantum Interpretation of Bunched Logic for Quantum Separation Logic, LICS ‘21: Proceedings of the 36th Annual ACM/IEEE Symposium on Logic in Computer Science 75 (2021) 1–14 [arXiv:2102.00329, doi:10.1109/LICS52264.2021.9470673]
Review and Exposition
Early general introductions and survey:
-
Itamar Pitowsky, Quantum Probability – Quantum Logic, Lecture Notes in Physics 321, Springer (1989) [doi:10.1007/BFb0021186]
(including discussion of quantum probability theory)
-
Roland Omnès, §5 of: The Interpretation of Quantum Mechanics, Princeton University Press (1994) [ISBN:9780691036694]
-
Pavel Pták , Sylvia Pulmannová , Orthomodular structures as quantum logics, Fundamental Theories of Physics 44 Kluwer, Springer (1991) [ISBN:978-0-7923-1207-9]
-
Kurt Engesser, Dov M. Gabbay, Daniel Lehmann (eds.) Handbook of Quantum Logic and Quantum Structures Elsevier (2009) [ISBN:9780080931661]
A bibliography of hundreds of works up to 1992:
- Mladen Pavičić, Bibliography on quantum logics and related structures, Int J Theor Phys 31 (1992) 373–455 [doi:10.1007/BF00739999, pdf]
See also:
-
Franco Strocchi, §2.5 in: An introduction to the mathematical structure of quantum mechanics, Advanced Series in Mathematical Physics 28, World Scientific (2008) [doi:10.1142/7038]
-
Wikipedia, Quantum logic
-
Stanford encyclopaedia of philosophy, Quantum logic and probability theory
Critique of Birkhoff-von Neumann logic in contrast to quantum information via dagger-compact categories:
- Samson Abramsky, Bob Coecke, Physics from Computer Science: a Position Statement, International Journal of Unconventional Computing 3 3 (2007) [pdf, ijuc-3-3-p-179-197]
Further exposition of non-cartesian monoidal categories as categorical semantics for quantum logic qua linear logic:
-
John Baez, Quantum Quandaries: a Category-Theoretic Perspective, in D. Rickles et al. (ed.) The structural foundations of quantum gravity, Clarendon Press (2006) 240-265 [arXiv:quant-ph/0404040, ISBN:9780199269693]
-
John Baez, Mike Stay, Physics, topology, logic and computation: a rosetta stone, (arxiv/0903.0340); in “New Structures for Physics”, ed. Bob Coecke, Lecture Notes in Physics 813, Springer (2011) 95-174 [doi:10.1007/978-3-642-12821-9]
Review of of quantum logic with an eye towards the EPR paradox and Bell's inequalities:
- Laura Molenaar, Quantum logic and the EPR paradox, Delft (2014) [uuid:cfee567c-425a-4b2d-9550-f7d7eea41b8b]
Further development
-
Chris Heunen, Quantifiers for quantum logic (arXiv:0811.1457)
-
John Harding, A link between quantum logic and categorical quantum mechanics, Int J Theor Phys (2009) 48: 769–802
-
Chris Heunen, Bart Jacobs, Quantum Logic in Dagger Kernel Categories, Order, July 2010, Volume 27, Issue 2, pp 177-212, (arXiv:0902.2355)
-
Gianpiero Cattaneo, Maria Luisa Dalla Chiara, Roberto Giuntini and Francesco Paoli, section 9 of Quantum Logic and Nonclassical Logics, p. 127 in Kurt Engesser, Dov M. Gabbay, Daniel Lehmann (eds.) Handbook of Quantum Logic and Quantum Structures: Quantum Logic, 2009 North Holland
-
Samson Abramsky, Temperley-Lieb Algebra: From Knot Theory to Logic and Computation via Quantum Mechanics, In Goong Chen, Louis Kauffman,
and Samuel Lomonaco (eds.), Mathematics of Quantum Computing and Technology, pages 415–458. Taylor and Francis, 2007. (arXiv:0910.2737)
-
Jean-Yves Girard, Lectures on Logic, European Mathematical Society 2011
-
Ugo Dal Lago, Claudia Faggian, On Multiplicative Linear Logic, Modality and Quantum Circuits [arXiv:1210.0613]
-
Bob Coecke, Chris Heunen, Aleks Kissinger, Compositional Quantum Logic (arXiv:1302.4900)
Discussion of Fock space-type free quantum field theory in linear logic is in
- Marcelo Fiore, Differential Structure in Models of Multiplicative Biadditive Intuitionistic Linear Logic (web)
The proposal that the internal logic of Bohr toposes is a good notion of quantum logic is made in
-
Chris Heunen, Klaas Landsman, Bas Spitters, A topos for algebraic quantum theory, Comm. Math. Phys. 291:63–110, 2009, free access doi, arXiv:0709.4364
-
Steve Vickers, slides from Midland Grad. School 2010, quantum topos theory, web, most relevant part IV: pdf
See also
-
Yuri Manin, A course in mathematical logic, Springer
-
Д.И. Блохинцев, Принципиальные вопросы квантовой механики, 1966, 162 с.
-
A. Sudbery, Quantum mechanics and the particles of nature, An outline for mathematicians, Camb. Univ. Press 1986
-
Stanford Encyclopedia of Philosophy, qm: von Neumann vs. Dirac,
Last revised on February 2, 2025 at 08:51:13. See the history of this page for a list of all contributions to it.