Redirected from "solid model topos".
Contents
under construction
Contents
Idea
The concept of solid topos is meant to be a characterization of gros toposes which further refines that of elastic toposes and cohesive toposes. The idea is that we may consistently regard the objects of such toposes as generalized spaces for some flavor of geometry, and that the axioms on the topos determine aspects of the geometric nature of these generalized spaces, as follows:
Definition
Definition
(solid topos)
Let be an elastic topos (this Def.) over a cohesive topos (this Def.). Then a solid topos or super-differentially cohesive topos over is a sheaf topos , which is
-
a cohesive topos over Set (this Def.),
-
an elastic topos over (this Def.).
-
equipped with a quadruple of adjoint functors (this Def.) to of the form
hence with and being fully faithful functors.
Lemma
(progression of (co-)reflective subcategories of solid topos)
Let be a solid topos (Def. ) over an elastic topos :
Then these adjoint functors arrange and decompose as shown in the following diagram:
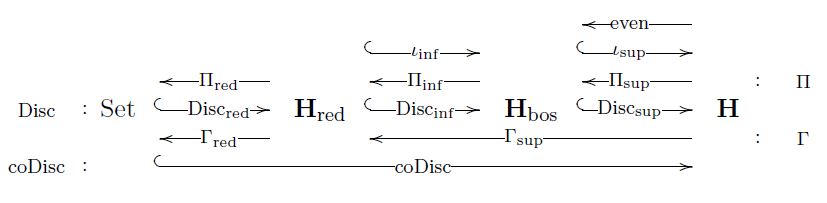
Here the composite adjoint quadruple
exhibits the cohesion of over Set, and the composite adjoint quadruple
exhibits the elasticity of over .
Definition
(adjoint modalities on solid topos)
Given a solid topos over (Def. ), composition of the functors in Lemma yields, via this Prop., the following adjoint modalities (this Def.)
Since and are fully faithful functors by assumption, these are (co-)modal operators (this Def.) on the cohesive topos, by this Prop..
We pronounce these as follows:
| fermionic modality | bosonic modality | rheonomy modality |
|---|
| | | |
and we refer to the corresponding modal objects (this Def.) as follows:
-
a -comodal object
is called a bosonic object;
-
a -modal object
is called a rheonomic object;
Proposition
(progression of adjoint modalities on solid topos)
Let be a solid topos (Def. ) and consider the adjoint modalities which it inherits
-
for being a cohesive topos, from this Def.,
-
for being an elastic topos, from this Def.,
-
for being a solid topos, from Def. :
| shape modality | flat modality | sharp modality |
|---|
| | | |
| | |
| reduction modality | infinitesimal shape modality | infinitesimal flat modality |
| | | |
| | |
| fermionic modality | bosonic modality | rheonomy modality |
| | | |
Then these arrange into the following progression, via the preorder on modalities from this Def.:
where we are displaying, for completeness, also the adjoint modalities at the bottom and the top (this Example).
Proof
By this Prop., it just remains to show that for all objects
-
is an -modal object, hence ,
-
is a bosonic object, hence .
The proof is directly analogous to the proof of that Prop., now using the decompositions from Lemma :
and
Examples
The sheaf topos of super formal smooth sets is solid over that of formal smooth sets, which is elastic over that of smooth sets, which is cohesive over Set.
See this Prop at geometry of physics – supergeometry.
