nLab
virtual double category

Idea

A virtual double category or $\mathrm{fc}$-multicategory is a common generalization of a monoidal category, a bicategory, a double category, and a multicategory. It contains:

• objects

• vertical arrows, which form a category

• horizontal arrows, which do not have identities or composites, and

• 2-cells which have

  • a horizontal source and target, which are vertical arrows,
  • a vertical target, which is a horizontal arrow, and
  • a vertical source, which is a composable string of horizontal arrows.

2-cells are usually drawn like this:

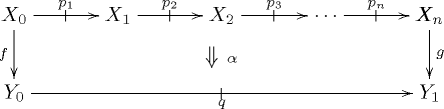
Note that this includes the case when $n=0$, i.e. a cell of “nullary” source. In this case, we must have $X_0=X_n$. Finally, the 2-cells can be composed in a more or less evident way, akin to composition in a multicategory:

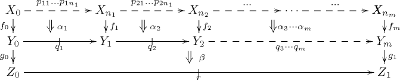
Virtual double categories are related to double categories precisely as ordinary multicategories are related to monoidal categories (see generalized multicategory and tensor product).

Definition

A virtual double category can be defined in two equivalent ways:

• It is a $T$-multicategory, in the sense of Leinster, relative to the monad $T$ on directed graphs whose algebras are categories. For this reason, Leinster originally called them fc-multicategories, where “fc” is a name for this monad $T$ which stands for “free-category.”

• It is a generalized multicategory, in the sense of Hermida, Cruttwell-Shulman, and others, relative to the monad $T$ on graphs-internal-to-Cat whose algebras are double categories. This is the origin of the name “virtual double category,” in line with the general terminology “virtual $T$-algebra” of Cruttwell-Shulman for such generalized multicategories.

We can also give an explicit definition, which was more or less already given in the “Idea” section: all that is missing are identities and associativity for 2-cell composition.

Examples

…

Higher categories of virtual double categories

There are notions of functor, transformation, and profunctor between virtual double categories. The neatest way to define all of these notions at once is to use the general framework of generalized multicategories: from the monad $\mathrm{fc}$ on the virtual equipment $\mathrm{Span}=\mathrm{Span}(\mathrm{Set})$ we can construct a new virtual equipment $\mathrm{vDblProf}=\mathrm{KMod}(\mathrm{Span},\mathrm{fc})$ whose objects are virtual double categories, whose arrows are functors between them, whose proarrows are profunctors between them, and whose cells are transformations. But we can also give explicit definitions of all of these notions.

Functors and transformations

A functor of virtual double categories is fairly obvious; it takes each kind of morphism/cell to the same kind, preserving sources, targets, composition, and identities.

The relevant transformations are a “virtual” version of vertical transformations between ordinary double categories. Specifically, a transformation $\alpha :F\to G$ has a vertical arrow component ${\alpha }_X:FX\to GX$ for each object $X$ of the domain, and a cell component

$$\begin{array}{ccc}FX& \stackrel{Fp}{\to }& FY\\ {}^{{\alpha }_X}\downarrow & {\Downarrow }^{{\alpha }_p}& {\downarrow }^{{\alpha }_Y}\\ GX& \underset{Gp}{\to }& GY\end{array}$$\array{F X & \overset{F p}{\to} & F Y\\ ^{\alpha_X}\downarrow & \Downarrow ^{\alpha_p}& \downarrow^{\alpha_Y}\\ G X& \underset{G p}{\to} & G Y}

for each horizontal arrow $p:X\to Y$ in the domain. These must be natural with respect to vertical composition of arrows and of 2-cells, where we must of course allow composites with arbitrary arities in the latter case.

Virtual double categories, functors, and transformations form a strict 2-category, and thus we can apply all notions of 2-category theory to it. In particular, we have a notion of a monad on a virtual double category, which is the starting point for one theory of generalized multicategories.

Profunctors

The profunctors between virtual double categories are a similar “virtualization” of the notion of double profunctor between double categories. Explicitly, a profunctor $H:C⇸D$ consists of:

• An ordinary profunctor $H_0:C_0⇸D_0$ between the categories of objects and vertical arrows.

• For each string of horizontal arrows $X_0\stackrel{p_1}{\to }{X}_1\to \dots \to X_n$ in $D$, each horizontal arrow $Y_0\stackrel{q}{\to }{Y}_1$ in $C$, and each pair of elements $f\in H_0(X_0,Y_0)$ and $g\in H_0(X_n,Y_1)$, a set of “hetero-cells” of shape

  

• The hetero-cells are acted on by the 2-cells of $D$ on the top, and by the 2-cells of $C$ on the bottom, in an evident way, respecting the given action of vertical arrows of $D$ and $C$ on the elements of $H_0$.

Every double profunctor induces such a profunctor in an evident way, but even if $C$ and $D$ are (non-virtual) double categories, not every “virtual double profunctor” from $C$ to $D$ need be a double functor; only those for which the “hetero-cells” also factor uniquely through the opcartesian cells in $D$ which make it “representable.”

As mentioned above in the context of the abstract definition, virtual double categories, functors, transformations, and profunctors form another virtual double category, which is in fact a virtual equipment.

Monads on virtual double categories

Definition

A monad on a virtual double category is a monad in the 2-category vDbl.

So a monad on a $X\in \mathrm{vDbl}$ consists of a functor

$$T:𝕏\to 𝕏$$T : \mathbb{X} \to \mathbb{X}

and transformations $\eta :\mathrm{Id}\to T$ and $\mu :TT\to T$ satisfying associativity and unitality.

Monoids and modules

Definition

For $T$ a monad on $𝕏\in$ vDbl, a $T$-monoid is

• an object $X_0\in 𝕏$;

• a horizontal morphism $X_0\stackrel{X}{⇸}T{X}_0$

• an action 2-morphism

  $$\begin{array}{ccccc}{X}_0& \stackrel{X}{⇸}& T{X}_0& \stackrel{TX}{⇸}{T}^2& X_0\\ {}^{=}\downarrow & & {\Downarrow }^{\overline{x}}& & {\downarrow }^{\mu }\\ X_0& & \underset{X}{⇸}& & T{X}_0\end{array}$$\array{ X_0 &\stackrel{X}{⇸} & T X_0 & \stackrel{T X}{⇸} T^2 & X_0 \\ {}^{\mathllap{=}}\downarrow && \Downarrow^{\bar x} && \downarrow^{\mathrlap{\mu}} \\ X_0 && \underset{X}{⇸} && T X_0 }

  and a unit 2-morphism

  $$\begin{array}{ccc}& & X_0\\ & {}^{=}\nearrow & {\Downarrow }^{\overline{x}}& {\searrow }^{\eta }\\ X_0& & \underset{X}{⇸}& & T{X}_0\end{array}$$\array{ && X_0 \\ & {}^{\mathllap{=}}\nearrow &\Downarrow^{\bar x}& \searrow^{\mathrlap{\eta}} \\ X_0 &&\underset{X}{⇸}&& T X_0 }

satisfying the evident compatibility conditions.

This is (CruttwellShulman, def. 4.2).

Definition

A $T$-monoid $X_0\stackrel{X}{⇸}T{X}_0$ is called normalized if its unit 2-morphism

$$\begin{array}{ccc}{X}_0& \stackrel{U_{X_0}}{\to }& X_0\\ {}^{=}\downarrow & & {dowmarrow}^{\eta }\\ X_0& \underset{X}{⇸}& T{X}_0\end{array}$$\array{ X_0 &\stackrel{U_{X_0}}{\to}& X_0 \\ {}^{\mathllap{=}}\downarrow && \dowmarrow^{\mathrlap{\eta}} \\ X_0 &\underset{X}{⇸}& T X_0 }

is a cartesian 2-morphism.

Generalized multicategories

Definition

A generalized multicategory is a normalized $T$-monoid for some monad $T$ on a virtual equipment $𝕏\in$ vDbl.

This is (CruttwellShulman, page 7).

Enriching categories

Virtual double categories can be viewed as “the natural place in which to enrich categories.” Specifically, for any set $A$, there is a virtual double category $A_{\mathrm{ch}}$ which has $A$ as its objects, only identity vertical arrows, exactly one horizontal arrow from every object to every other object, and exactly one 2-cell in every possible niche. For any other virtual double category $W$, a functor $A_{\mathrm{ch}}\to W$ of virtual double categories is the same as a $W$-enriched category with object set $A$.

References

• Tom Leinster, Higher Operads, Higher Categories, link, arXiv:0305049

• Geoff Cruttwell and Mike Shulman, A unified framework for generalized multicategories, arXiv:0907.2460