Schreiber M/F-Theory as Mf-Theory
An article that we have written:
-
M/F-Theory as -Theory
Reviews in Mathematical Physics
35 10 (2023)
download:
Abstract. In the quest for mathematical foundations of M-theory, the Hypothesis H that fluxes are quantized in Cohomotopy theory, implies, on flat but possibly singular spacetimes, that M-brane charges locally organize into equivariant homotopy groups of spheres.
Here we show how this leads to a correspondence between phenomena conjectured in M-theory and fundamental mathematical concepts/results in stable homotopy, generalized cohomology and Cobordism theory :
-
stems of homotopy groups correspond to charges of probe p-branes near black n-branes;
-
stabilization within a stem is the boundary-bulk transition;
-
the Adams d-invariant measures G4-flux;
-
trivialization of the d-invariant corresponds to -flux;
-
refined Toda brackets measure -flux;
-
the refined Adams e-invariant sees the -charge lattice;
-
vanishing Adams e-invariant implies consistent global -fields;
-
Conner-Floyd’s e-invariant is the -flux seen in the Green-Schwarz mechanism;
-
the Hopf invariant is the M2-brane Page charge (-flux);
-
the Pontrjagin theorem associates the polarized braneworldvolumes sourcing all these charges.
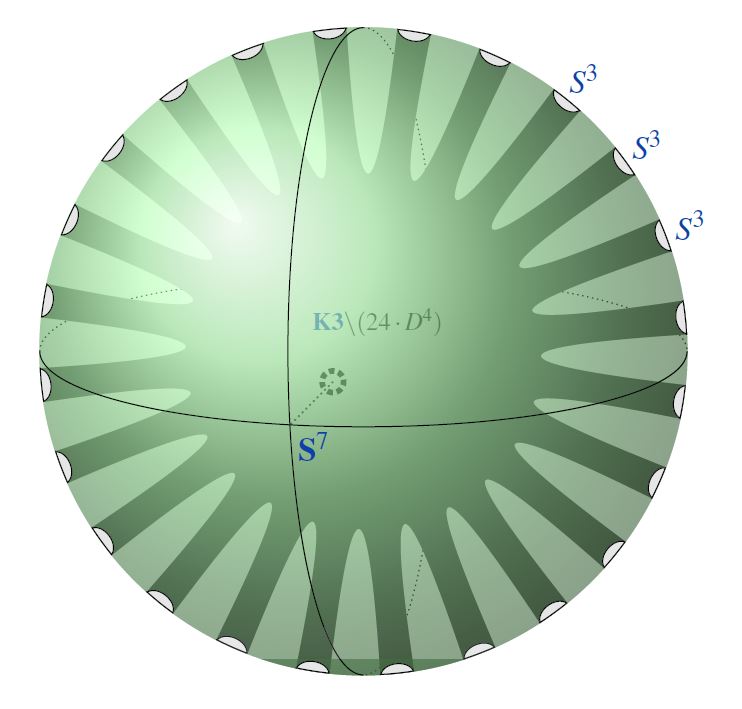
In particular, spontaneous K3-reductions with 24 branes are singled out from first principles:
-
Cobordism in the third stable stem witnesses spontaneous KK-compactification on K3-surfaces;
-
the order of the third stable stem implies the 24 NS5/D7-branes in M/F-theory on K3.
Finally, complex-oriented cohomology emerges from Hypothesis H, connecting it to all previous proposals for brane charge quantization in the chromatic tower: in ordinary cohomology, in K-theory, in elliptic cohomology, etc.:
-
quaternionic orientations correspond to unit -fluxes near M2-branes;
-
complex orientations lift these unit -fluxes to heterotic M-theory with heterotic line bundles.
In fact, we find quaternionic/complex Ravenel-orientations bounded in dimension; and we find the bound to be 10, as befits spacetime dimension 10+1.
Concluding remarks. Since the Pontrjagin theorem identifies Cohomotopy theory with framed Cobordism cohomology, the statement of Hypothesis H is equivalently:
- M-Brane charge is quantized in framed Cobordism cohomology.
But since stable Cohomotopy/framed Cobordism is the initial multiplicative cohomology theory, every other multiplicative cohomology serves to approximate brane charge quantization in Cohomotopy. Specifically, existence of universal -fluxes near M2-branes forces brane charge observation through quaternionic-orientated – in particular complex-orientated – multiplicative cohomology theories.
Moreover, initial among oriented cohomology theories are again Cobordism cohomology theories, namely quaternionic Coordism MSp and complex cobordism MU, respectively. And indeed, one may recover observations of charges in Cohomotopy, hence in framed Cobordism, from their observations in unitary Cobordism – this is the statement of the Adams-Novikov spectral sequence:
- M-Brane charge quantization may be observed in complex Cobordism.
Which is to say that, with Hypothesis H, M-brane charge is not only fundamentally in framed Cobordism, but, in the presence of black M2-brane sources, M-brane charges are canonically approximated/perceived through other flavors of Cobordism cohomology , such as quaternionic and unitary cobordism, but also, for instance, special unitary Cobordism MSU, (which connects with Calabi-Yau KK-compactifications).
In summary and in the form of a broad slogan, Hypothesis H implies that:
- M-brane charge quantization is seen in Cobordism theories.
hence that
- M-theory is controlled by -theory.
This is a direct analogue – a refinement – of the traditional conjecture that D-brane charge is quantized in topological K-theory. Indeed, if M-brane charge is in Cobordism theory, then perceiving it through the lens of K-orientations means to approximate it by K-theory.
Related articles on Hypothesis H:
-
Twisted Cohomotopy implies M-theory anomaly cancellation on 8-manifolds
-
Equivariant Cohomotopy implies orientifold tadpole cancellation
-
Differential Cohomotopy implies intersecting brane observables
-
Twisted Cohomotopy implies twisted String structure on M5-branes
-
Twistorial Cohomotopy implies Green-Schwarz anomaly cancellation
Last revised on November 21, 2023 at 09:17:27. See the history of this page for a list of all contributions to it.