nLab Adams e-invariant

Idea

The $e$-invariant (Adams 66, Sections 3,7, short for “extension invariant”, see Def. below) is the second in a sequence of homotopy invariants of “stable maps”, i.e. of morphisms in the stable homotopy category (in particular: of stable homotopy groups of spheres), being elements of Ext-groups between the homology groups/cohomology groups of the domain and codomain of the map, with respect to some suitable choice of Whitehead-generalized cohomology theory $E$.

The previous invariant in the sequence is the d-invariant, the next is the f-invariant. These are the elements that appear in the first lines on the second page of the $E$-Adams spectral sequence for $[X,Y]_\bullet$.

Definition

Let $X \overset{f}{\longrightarrow} Y$ be morphism in the stable homotopy category out of a finite spectrum $X$ (for instance the image under suspension $\Sigma^\infty$ of a morphism in the classical homotopy category of pointed homotopy types out of a finite CW-complex).

Let $E$ be a multiplicative cohomology theory, such that the d-invariant of $f$ in $E$ vanishes, hence such that pullback $f^\ast \;\colon\; E^\bullet(Y) \to E^\bullet(X)$ in $E$-cohomology is the zero morphism.

The archetypical example is $f \;\colon\; S^{2n-1} \to S^{2n}$ a map out of an odd-dimensional sphere and $E = KU$ complex topological K-theory.

As an extension of generalized Adams-operation modules

Definition

(e-invariant as extension class in E-cohomology)

Writing $C_f$ for the homotopy cofiber of $f$

$$\cdots \to X \overset{f}{\longrightarrow} Y \overset{}{\longrightarrow} C_f \overset{}{\longrightarrow} \Sigma X \to \cdots \,,$$

this implies that the long exact sequence in cohomology corresponding to the pair $(Y, C_f)$ truncates to a short exact sequence of the form

(1)$$0 \to E^\bullet(\Sigma X) \overset{}{\longrightarrow} E^\bullet(C_f) \overset{}{\longrightarrow} E^\bullet(Y) \to 0 \,.$$

This is hence an extension of $E^\bullet(Y)$ by $E^\bullet(\Sigma X)$ in any category in which $f^\ast$ is a homomorphism, for instance that of modules over the E-Steenrod algebra. For the case of $E = KU$ take the category of graded abelian groups equipped with Adams operations.

Thus this short exact sequence defines an element in the Ext group formed in this category

(2)$$e(f) \;\in\; Ext^1\big( E^\bullet(Y), \, E^\bullet(\Sigma X) \big)$$

and this is the e-invariant of $f$ seen in $E$-theory.

(Adams 66, Section 3, p. 27, review includes BL 09, Sec. 2).

For $E = KU$

As an extension of K-groups with Adams operations

We discuss this in more detail for the case of complex topological K-theory $E = KU$, and for $f \;\colon\; S^{2(n + \bullet)-1} \to S^{2n}$ a map between spheres; and we show how the resulting extension is characterized by a single rational number modulo the integers, this being the e-invariant in the form of a Q/Z-valued character

$$e_{\mathbb{C}} \;\colon\; \pi^s_{\bullet} \overset{\;\;\;\;\;}{\longrightarrow} \mathbb{Q}/\mathbb{Z}$$

on stable homotopy groups of spheres (Def. below).

We follow Hopkins-Mathew 12, Lecture 11.

Abelian groups with Adams operations

Definition

(abelian group with Adams operations)

We say that an abelian group with Adams operation $\big(A,\{\psi_A^k\}_{k \in \mathbb{N}}\big)$ is an abelian group $A$ equipped with an action of the multiplicative monoid $(\mathbb{N}, \cdot)$ of natural numbers, hence equipped with group homomorphisms

$$\psi_A^k \;\colon\; A \to A \,, \;\;\;\;\;\;\; \text{for all} \; k \in \mathbb{N}$$

such that

(3)$$\psi_A^{k_1} \circ \psi_A^{k_2} \;=\; \psi_A^{ k_1 \cdot k_2 } \,, \;\;\;\;\;\;\;\;\; \text{for all} \; k_1, k_2 \,\in\, \mathbb{N} \,.$$

Moreover, for $\big(A,\{\psi_A^k\}_{k \in \mathbb{N}}\big), \, \big(A',\{\psi_{A'}^k\}_{k \in \mathbb{N}}\big)$ two abelian groups with Adams operations, a homomorphism between them is a group homomorphism (a linear map) $\phi \;\colon\; A \to A'$ that respects these operations, hence such that the following squares commute:

(4)$$\array{ A &\overset{\;\;\;\phi\;\;\;}{\longrightarrow}& A' \\ {}^{\mathllap{ \psi^k_A }} \big\downarrow && \big\downarrow {}^{\mathrlap{\psi_{A'}^k}} \\ A &\overset{\;\;\;\phi\;\;\;}{\longrightarrow}& A' \,, } \;\;\;\;\;\;\;\; \text{for all} \; k \in \mathbb{N} \,.$$

This makes an abelian category which we denoted $Ab_{Adams}$, canonically equipped with a forgetful functor to Ab:

(5)$$\array{ Ab_{Adams} &\overset{\;\;\;\;\;\;}{\longrightarrow}& Ab \\ \big( A, \, \{\psi^k_A\}_{k \in \mathbb{N}} \big) &\mapsto& A \,. }$$

Example

For $n \in \mathbb{N}$, the additive abelian group of integers $\mathbb{Z}$ becomes an abelian group with Adams operations

$$\mathbb{Z}(n) \;\coloneqq\; \big( \mathbb{Z},\, \{\psi^k_{\mathbb{Z}(n)}\} \big) \,,$$

in the sense of Def. , by setting

$$\array{ \mathbb{Z} & \overset{\;\;\; \psi^k_{\mathbb{Z}(n)}\;\;\;}{\longrightarrow} & \mathbb{Z} \\ r &\mapsto& k^n \cdot r \,. }$$

Example

(Adams operations on complex topological K-theory groups)

For $X$ a compact pointed topological space, the complex topological K-theory group $K(X)$ becomes an abelian group with Adams operations in the sense of Def. , via the actual Adams operations,

$$K(X), \widetilde K(X) \;\in\; Ab_{Adams}$$

and hence so does the reduced K-theory $\widetilde K(X)$:

$$\array{ \widetilde K(X) &\overset{\;\;ker(i^\ast)\;\;}{\longrightarrow}& K(X) &\overset{\;i^\ast\;}{\longrightarrow}& K(\ast) \\ \big\downarrow {}^{\mathrlap{\psi^k_{\widetilde K(X)}}} && \big\downarrow {}^{\mathrlap{\psi^k_{K(X)}}} && \big\downarrow {}^{\mathrlap{\psi^k_{K(\ast)}}} \\ \widetilde K(X) &\underset{\;\;ker(i^\ast)\;\;}{\longrightarrow}& K(X) &\underset{\;i^\ast\;}{\longrightarrow}& K(\ast) \,, }$$

Moreover, for each (pointed) continuous function $X \overset{f}{\longrightarrow} Y$ the corresponding pullback in cohomology respects the Adams operations and hence yields a homomorphism (4):

(6)$$\widetilde K(X) \overset{\;\;f^\ast\;\;}{\longrightarrow} \widetilde K(Y) \,, \;\;\;\; \in \; Ab_{Adams} \,.$$

Proposition

(Adams operations on complex topological K-theory of n-spheres)

For $n \in \mathbb{N}$, the Adams operations on the reduced K-theory (Example ) of the 2n-sphere are given by:

$$\array{ \widetilde K \big( S^{2n} \big) & \overset{ \;\;\; \psi^k\;\;\; }{\longrightarrow} & \widetilde K \big( S^{2n} \big) \\ V &\mapsto& k^n \cdot V }$$

and hence are isomorphic in $Ab_{Adams}$ (Def. ) to the objects from Example :

$$\widetilde K \big( S^{2n} \big) \;\simeq\; \mathbb{Z}(n) \;\;\;\; \in \; Ab_{Adams} \,.$$

The Adams $e_{\mathbb{C}}$-invariant in $\mathbb{Q}/\mathbb{Z}$

Example

(the defining short exact sequence in complex topological K-theory)

For $n, n' \,\in\, \mathbb{N}$ let

$$f \;\colon\; S^{2(n + n') - 1} \longrightarrow S^{2n}$$

be a continuous function between spheres (representing its image in the classical homotopy category and in fact in the stable homotopy category, which is all that its image in a Whitehead-generalized cohomology theory such as complex topological K-theory depends on), such that the d-invariant of $f$ vanishes under complex topological K-theory $E = KU$, hence such that the pullback $f^\ast$ is the zero map in K-theory:

$$d(f) \;\coloneqq\; f^\ast \;=\; 0 \;\;\;\colon\; \widetilde K\big(S^{2n}\big) \longrightarrow \widetilde K\big( S^{2(n + n') - 1} \big) \,.$$

Writing $C_f$ for the homotopy type of the homotopy cofiber/attaching space of $f$:

(7)$$\array{ S^{2(n + n') - 1} &\longrightarrow& \ast \\ {}^{\mathllap{f}} \big\downarrow & {}^{_{(hpo)}} & \big\downarrow \\ S^{2n} &\underset{i_{2n}}{\longrightarrow}& C_f \\ {}^{} \big\downarrow & {}^{_{(hpo)}} & \big\downarrow {}^{\mathrlap{ p_{2(n+n')} }} \\ \ast &\longrightarrow& S^{2(n + n')} } \;\;\;\;\;\;\;\; \simeq \;\;\;\;\;\;\;\; \array{ S^{2(n + n') - 1} &\longrightarrow& D^{2(n + n')} \\ {}^{\mathllap{f}} \big\downarrow & {}^{_{(po)}} & \big\downarrow \\ S^{2n} &\underset{i_{2n}}{\longrightarrow}& C_f \\ {}^{} \big\downarrow & {}^{_{(po)}} & \big\downarrow {}^{\mathrlap{ p_{2(n+n')} }} \\ \ast &\longrightarrow& S^{2(n + n')} }$$

this implies that the long exact sequence in cohomology induced by the CW-pair $S^{2n} \hookrightarrow C_f$ truncates to the short exact sequence (1), here regarded, by Example , in the abelian category $Ab_{Adams}$ of abelian groups with Adams operations (Def. ):

(8)$$\array{ 0 &\to& \widetilde K\big( S^{2(n + n')} \big) &\overset{\;\;\; p_{2(n+n')}^\ast \;\;\;}{\longrightarrow}& \widetilde K\big( C_f \big) &\overset{\;\;\; i_{2n}^\ast \;\;\;}{\longrightarrow}& \widetilde K\big( S^{2n} \big) &\to& 0 \\ && \big\downarrow {}^{\mathrlap{\simeq}} && \big\downarrow {}^{\mathrlap{=}} && \big\downarrow {}^{\mathrlap{\simeq}} \\ 0 &\to& \mathbb{Z}(n + n') &\underset{\;\;\; \;\;\;\; \;\;\;}{\longrightarrow}& \widetilde K\big( C_f \big) &\underset{\;\;\; \;\;\;\; \;\;\;}{\longrightarrow}& \mathbb{Z}(n) &\to& 0 } \;\;\;\;\;\;\;\; \in \; Ab_{Adams} \,,$$

where in the second line we have identified the outer groups via Prop. .

By definition of Ext-groups, the isomorphism class of this short exact sequence with the outer groups fixed is an element

(9)$$e_{\mathbb{C}}(f) \;\;\in\;\; Ext^1_{Ab_{Adams}} \big( \mathbb{Z}(n), \, \mathbb{Z}(n + n') \big) \,.$$

This is the Adams e-invariant of $f$ as seen in complex topological K-theory; in specialization of (2).

More concretely, it turns out that the extension (9) is completely characterized by a single rational number modulo this integers. This we discuss next (Def. below).

Remark

(extension after forgetting the Adams module structure is trivial)

After forgetting the action of the Adams operations via (5), the sequence (8) is still a short exact sequence, now of plain abelian groups. However, since $Ext^1_{Ab}(\mathbb{Z},-) = 0$ (this Prop.), it is necessarily trivial as an extension, showing that the underlying abelian cohomlogy group of the cofiber space is just

(10)$$\array{ \mathbb{Z} \oplus \mathbb{Z} & \simeq & \widetilde K \big( S^{2n} \big) \,\oplus\, \widetilde K \big( S^{2(n + n')} \big) & \simeq & \widetilde K \big( C_f \big) \\ \big( 1, \, 1 \big) &\mapsto& \big( \Sigma^{2n} 1, \, \Sigma^{2(n + n')} 1 \big) &\mapsto& \big( V_{2n}, \, V_{2(n+n')} \big) } \;\; \;\in\; Ab \,,$$

where $V_{2(n + n')} \;\coloneqq\; p_{2(n+n')}^\ast \Sigma^{2(n+n')} 1$ and where $V_{2n}$ is a choice of lift of $\Sigma^{2n} 1$ through $i_{2n}^\ast$ in the short exact sequence (8):

(11)$$\array{ 0 \to & \widetilde K\big( S^{2(n+n')} \big) & \overset{p^\ast_{2(n+n')}}{\longrightarrow} & \widetilde K\big( C_f \big) & \overset{i^\ast_{2n}}{\longrightarrow} & \widetilde K\big( S^{2n} \big) & \to 0 \\ & \Sigma^{2(n+n')} 1 &\mapsto& V_{2(n+n')} \\ & && V_{2n} &\mapsto& \Sigma^{2n} 1 \,. }$$

Notice that the isomorphism (10) depends on a choice of splitting (11) of the short exact sequence (8) in Ab: any two choices $V_{2n}$, $V'_{2n}$ differ by a multiple $s \in \mathbb{Z}$ of the generator $V_{2(n + n')}$:

(12)$$V'_{2n} \;=\; V_{2n} + s \cdot V_{2(n + n')} \,.$$

Conversely, this means that all the information in the extension (8) is in how the Adams operations act on the K-theory of the cofiber space:

Definition

(e-invariant in complex topological K-theory as rational number modulo integers)

Given a map $f \;\colon\; S^{2(n + n') - 1} \longrightarrow S^{2n}$ with vanishing $KU$-d-invariant, as in Example , we have by Remark that the Adams operations (Example ) on the cofiber space $C_f$ (7) must be of the following form (Adams 66, Prop. 7.5, (7.10) (9.2)):

(13)$$\array{ \widetilde K\big( C_f\big) &\overset{ \;\;\; \psi^k\;\;\; }{\longrightarrow}& \widetilde K\big( C_f\big) \\ V_{2n} &\mapsto& k^n \cdot V_{2n} \;+\; {\color{blue} \mu_k(f) } \cdot V_{2(n+ n')} \\ V_{2(n + n')} &\mapsto& k^{n + n'} \cdot V_{2(n + n')} \;\;\;\;\;\;\;\; \,. }$$

Namely, the first summands on the right are constrained to be as shown, by Prop. and using that pullback in cohomology $i^\ast_{2n}$, $p^\ast_{2(n + n')}$(6) respects the Adams operations (Example ); while the second summand, which vanishes under $i^\ast_{2n}$, must be some multiple

$$\mu_k(f) \;\in\; \mathbb{Z}$$

of the only other generator $V_{2(n + n')}$ (10). This $\mu$ is the only part of the data that is not completely fixed by the Adams module structure, and which may depend on the map $f$.

We say that the Adams e-invariant of $f$ is this multiple $\mu$, normalized as a rational number as follows, and then regarded modulo addition of integers as an element in Q/Z:

(14)$$e_{\mathbb{C}}(f) \;\coloneqq\; \left[ \frac{ \mu_k(f) }{ k^{n} \big( k^{n'} - 1 \big) } \right] \;\; \in \;\; \mathbb{Q}/\mathbb{Z} \,.$$

Proposition

(e-invariant as rational number modulo integers is well defined)

The e-invariant $e_{\mathbb{C}}(f)$ (14) from Def. is well-defined, in that it is

1. independent of the choice of splitting $\Sigma^{2n} 1 \,\mapsto\, V_{2n}$ in (10);

2. independent of the choice of $k$ on the right of (14).

Proof

On 1. Under a different choice of splitting, $V_{2n}$ changes to (12)

$$V'_{2n} \;=\; V_{2n} + s \cdot V_{2(n + n')}$$

for some $s \in \mathbb{Z}$. By inspection of (13) this implies that $\mu_k(f)$ changes to

$$\mu'_k(f) \;=\; \mu_k(f) + s \cdot \big( k^{n + n'} - k^n \big) \,;$$

and so in (14) we have

$$e'_{\mathbb{C}}(f) \;=\; \left[ \frac{ \mu'_k(f) }{ k^n(k^{n'} -1 ) } \right] \;=\; \left[ \frac{ \mu_k(f) }{ k^n(k^{n'} -1 ) } + s \right] \;=\; \left[ \frac{ \mu_k(f) }{ k^n(k^{n'} -1 ) } \right] \;=\; e_{\mathbb{C}}(f) \,.$$

On 2. Use the commutativity (3) of the Adams operation together with the formula (13) to find for any $k_1, k_2 \,\in\, \mathbb{N}$:

$$\begin{aligned} & \phantom{\;=\;\;} \psi^{k_1} \circ \psi^{k_2} \big( V_{2n} \big) \\ & \;=\; \psi^{k_2} \circ \psi^{k_1} \big( V_{2n} \big) \\ \\ \Leftrightarrow \;\;\; & \phantom{\;=\;\;} \psi^{k_1} \big( k_2^n \cdot V_{2n} + \mu_{k_2}(f) \cdot V_{2(n + n')} \big) \\ & \;=\; \psi^{k_2} \big( k_1^n \cdot V_{2n} + \mu_{k_1}(f) \cdot V_{2(n + n')} \big) \\ \\ \Leftrightarrow \;\;\; & \phantom{\;=\;\;} (k_1 k_2)^n \cdot V_{2n} + \Big( k_2^n \mu_{k_1}(f) + k_1^{n + n'} \mu_{k_2}(f) \Big) \cdot V_{2(n + n')} \\ & \;=\; (k_1 k_2)^n \cdot V_{2n} + \Big( k_1^n \mu_{k_2}(f) + k_2^{n + n'} \mu_{k_1}(f) \Big) \cdot V_{2(n + n')} \\ \\ \Leftrightarrow \;\;\; & \phantom{\;=\;\;} k_1^n \big( k_1^{n'} - 1 \big) \mu_{k_2}(f) \\ & \;=\; k_2^n \big( k_2^{n'} - 1 \big) \mu_{k_1}(f) \\ \\ \Leftrightarrow \;\;\; & \phantom{\;=\;\;} \frac{ \mu_{k_1}(f) }{ k_1^n \big( k_1^{n'} - 1 \big) } \\ & \;=\; \frac{ \mu_{k_2}(f) }{ k_2^n \big( k_2^{n'} - 1 \big) } \end{aligned}$$

As the top degree Chern character on cofiber space

Proposition

(Q/Z-valued e-invariant is top-degree coefficient of Chern character on cofiber space)

In the situation of Example , with

$$f \;\colon\; S^{2(n+n')-1 } \longrightarrow S^{2n}$$

a map between spheres, and with $V_{2n} \,\in\, \widetilde K\big( C_f \big)$ any lift (11) of $\Sigma^{2 n} 1 \,\in\, \widetilde K \big( S^{2n} \big)$ to its homotopy cofiber space, we have that the e-invariant $e_{\mathbb{C}}(f)$ (Def. ) is equivalently the evaluation modulo integers of the Chern character $ch(V_{2n}) \,\in\, H^{ev}\big( C_f;\, \mathbb{Q} \big)$ on the fundamental class of the cofiber space:

$$\exp \left( 2 \pi \mathrm{i} \int_{C_f} ch\big( V_{2n} \big) \right) \;=\; \exp \left( 2 \pi \mathrm{i} \, { \color{blue} e_{\mathbb{C}}(f) } \right) \;\;\; \in \mathrm{U}(1) \,.$$

Adams 66, Prop. 7.5

Proof

By (13) we have, now in matrix calculus-notation:

$$\psi^k \;\colon\; \left[ \array{ V_{2 n } \\ V_{2(n + n')} } \right] \;\;\; \mapsto \;\;\; \left[ \array{ k^n & e(f) \, k^n (k^{n'} - 1) \\ 0 & k^{n + n'} } \right] \cdot \left[ \array{ V_{2 n } \\ V_{2(n + n')} } \right] \;\;\;\;\; \in \; \widetilde K\big( C_f \big) \,.$$

This matrix has two eigenvectors over the rational numbers (in general). Therefore we now consider the image of these K-theory classes under the Chern character map

$$ch \;\colon\; \widetilde K\big( C_f \big) \longrightarrow H^{ev}\big( C_f;\, \mathbb{Q}\big) \,.$$

Since the Adams operations are compatible with the Chern character, we then have the following eigenvectors of the Adams operations under $ch$:

(15)$$\psi^k_H \;\;\colon\;\; \left\{ \array{ ch \big( V_{2 n} \big) - e(f) \cdot ch \big( V_{2(n + n')} \big) & \mapsto & k^{n } & \cdot & \big( ch ( V_{2 n} ) - e(f) \cdot ch ( V_{2(n + n')} ) \big) \\ ch ( V_{2(n+n')} ) & \mapsto & k^{n + n'} & \cdot & ch ( V_{2 (n + n')} ) } \right. \;\;\;\; \in \; H^{ev}\big( C_f; \, \mathbb{Q} \big)/H^{2(n+n')}\big( C_f; \, \mathbb{Z} \big) \,.$$

Here, since $V_{2n}$ is well defined modulo addition (12) of integral multiples of $V_{2(n+n')}$, and since

(16)$$ch\big( V_{2(n+n')} \big) \;=\; 1 \,\in\, \mathbb{Z} \,\simeq\, H^{2(n+n')}\big( C_f;\, \mathbb{Z} \big) \,,$$

this expression (15) is well-defined in ordinary rational cohomology in even degrees modulo integral cohomology in top degree.

But since the eigenvectors of $\psi^k_H$ to eigenvalue $k^r$ are precisely the ordinary cohomology classes in homogeneous degree $H^{2r}\big( C_f;\, \mathbb{Q} \big) \,\subset\, H^{ev}\big( C_f;\, \mathbb{Q} \big)$ (see there), this means that

$$ch \big( V_{2n} \big) \;\;=\;\; \underset{ \in \; H^{2n}\big( C_f; \, \mathbb{Q} \big) }{ \underbrace{ ch \big( V_{2n} \big) - e(f) \cdot ch \big( V_{2(n+n')} \big) } } \;+\; \underset{ \in \; H^{2(n + n')}\big( C_f; \, \mathbb{Q}/\mathbb{Z} \big) }{ \underbrace{ e(f) \cdot ch \big( V_{2(n+n')} \big) \,. } }$$

(See also Conner-Floyd 66, p. 100.)

The evaluation of this cohomology class on the fundamental class of $C_f$ picks out the coefficient of $ch\big( V_{2(n+n')} \big)$, by (16):

$$\int_{C_f} ch \big( V_{2n} \big) \;=\; e(f) \;\;\; \in \; \mathbb{Q}/\mathbb{Z} \,,$$

and hence the claim follows.

Remark

The analogue statement of Prop. for the $e_{\mathbb{R}}$-invariant (Def. ) may fail:

The $e_{\mathbb{R}}$-invariant defined in terms of Adams operations (Def. ) is $c$ times the top degree coefficient of the Chern character on $K \mathrm{O} \to K \mathrm{U}$ (the Pontrjagin character) with (Adams 66 (7.3)):

1. $c = 1$ for $(n + n') = \,0\, mod \, 8$ (here they coincide)

2. $c = \tfrac{1}{2}$ for $(n + n') = \,4\, mod \, 8$ (here the $e_{\mathbb{R}}$-invariant is finer).

Similarly (Adams 66 Prop. 7.14):

• the $e_{\mathbb{R}}$-invariant equals the $e_{\mathbb{C}}$-invariant for $n' = \,0\, mod \, 8$,

• but equals $\tfrac{1}{2}e_{\mathbb{C}}$ for $n + n' = \,4\, mod \, 8$ .

This means that the $e_{\mathbb{R}}$-invariant is finer than the $e_{\mathbb{C}}$-invariant.

As a cobordism invariant of U-manifolds with framed boundary

We discuss how the e-invariant in its Q/Z-incarnation (Def. ) has a natural formulation in cobordism theory (Conner-Floyd 66).

This is Prop. below; but first to recall some background:

Remark

In generalization to how the U-bordism ring $\Omega^U_{2k}$ is represented by homotopy classes of maps into the Thom spectrum MU, so the (U,fr)-bordism ring $\Omega^{U,fr}_{2k}$ is represented by maps into the quotient spaces $MU_{2k}/S^{2k}$ (for $S^{2k} = Th(\mathbb{C}^{k}) \to Th( \mathbb{C}^k \times_{U(k)} E U(k) ) = MU_{2k}$ the canonical inclusion):

(17)$$\Omega^{(U,fr)}_\bullet \;=\; \pi_{\bullet + 2k} \big( MU_{2k}/S^{2k} \big) \,, \;\;\;\;\; \text{for any} \; 2k \geq \bullet + 2 \,.$$

(Conner-Floyd 66, p. 97)

Remark

The bordism rings for MU, MUFr and MFr sit in a short exact sequence of the form

(18)$$0 \to \Omega^U_{\bullet+1} \overset{i}{\longrightarrow} \Omega^{U,fr}_{\bullet+1} \overset{\partial}{ \longrightarrow } \Omega^{fr}_\bullet \to 0 \,,$$

where $i$ is the evident inclusion, while $\partial$ is restriction to the boundary.

(By this Prop. at MUFr.)

In particular, this means that $\partial$ is surjective, hence that every $Fr$-manifold is the boundary of a (U,fr)-manifold.

Proposition

(e-invariant is Todd class of cobounding (U,fr)-manifold)

Evaluation of the Todd class on (U,fr)-manifolds yields rational numbers which are integers on actual $U$-manifolds. It follows with the short exact sequence (18) that assigning to $Fr$-manifolds the Todd class of any of their cobounding $(U,fr)$-manifolds yields a well-defined element in Q/Z.

Under the Pontrjagin-Thom isomorphism between the framed bordism ring and the stable homotopy group of spheres $\pi^s_\bullet$, this assignment coincides with the Adams e-invariant in its Q/Z-incarnation:

(19)$$\array{ 0 \to & \Omega^U_{\bullet+1} & \overset{i}{\longrightarrow} & \Omega^{U,fr}_{\bullet+1} & \overset{\partial}{ \longrightarrow } & \Omega^{fr}_\bullet & \simeq & \pi^s_\bullet \\ & \big\downarrow{}^{\mathrlap{Td}} && \big\downarrow{}^{\mathrlap{Td}} && \big\downarrow{}^{} && \big\downarrow{}^{e} \\ 0 \to & \mathbb{Z} &\overset{\;\;\;\;\;}{\hookrightarrow}& \mathbb{Q} &\overset{\;\;\;\;}{\longrightarrow}& \mathbb{Q}/\mathbb{Z} &=& \mathbb{Q}/\mathbb{Z} } \,,$$

(Conner-Floyd 66, Theorem 16.2)

The first step in the proof of (19) is the observation (Conner-Floyd 66, p. 100-101) that the representing map (17) for a $(U,fr)$-manifold $M^{2k}$ cobounding a $Fr$-manifold represented by a map $f$ is given by the following homotopy pasting diagram (see also at Hopf invariant – In generalized cohomology):

from SS21

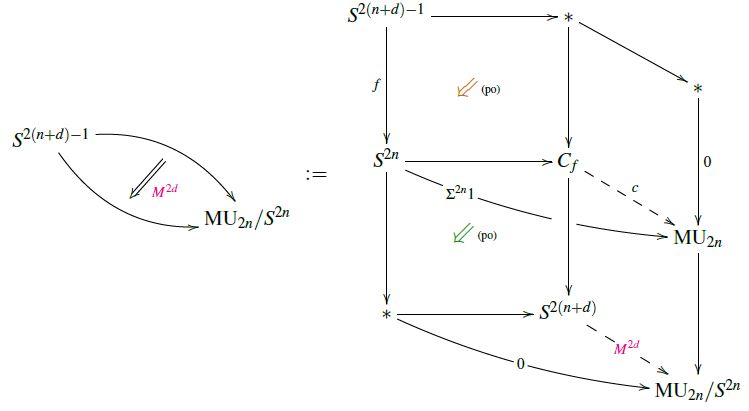
For $E = KO$

The Adams $e_{\mathbb{R}}$-invariant in $\mathbb{Q}/\mathbb{Z}$

Definition

Definition (via Adams operations) applies verbatim also with real (i.e. orthogonal) topological K-theory KO in place of complex topological K-theory KU. The resulting invariant is denoted $e_{\mathbb{R}}$ (Adams 66, p. 39).

But beware that $e_{\mathbb{R}}$ may fail to be equal to the coefficient of the top degree Chern character on KO (the Pontrjagin character), see Remark . That is, in fact, what makes $e_{\mathbb{R}}$ a finer invariant: It is either equal to $e_{\mathbb{C}}$ or to $\tfrac{1}{2}e_{\mathbb{C}}$. (Adams 66 (7.3)).

As a cobordism invariant of $SU$-manifolds with framed boundary

An analogous but finer version of the cobordism-theoretic construction (above) works for special unitary group-structure instead of unitary group-structure and in dimensions $8\bullet + 4$:

Since on $(8 \bullet + 4)$-dimensional $SU$-manifolds the Todd class is divisible by 2 Conner-Floyd 66, Prop. 16.4, we have (Conner-Floyd 66, p. 104) the following variant of (19):

(20)$$\array{ 0 \to & \Omega^{SU}_{8\bullet+4} & \overset{i}{\longrightarrow} & \Omega^{SU,fr}_{8\bullet+4} & \overset{\partial}{ \longrightarrow } & \Omega^{fr}_{8 \bullet + 3} & \simeq & \pi^s_{8 \bullet + 3} \\ & \big\downarrow{}^{\tfrac{1}{2}\mathrlap{Td}} && \big\downarrow{}^{\tfrac{1}{2}\mathrlap{Td}} && \big\downarrow{}^{} && \big\downarrow{}^{e_{\mathbb{R}}} \\ 0 \to & \mathbb{Z} &\overset{\;\;\;\;\;}{\hookrightarrow}& \mathbb{Q} &\overset{\;\;\;\;}{\longrightarrow}& \mathbb{Q}/\mathbb{Z} &=& \mathbb{Q}/\mathbb{Z} } \,.$$

This produces $e_{\mathbb{R}}$, the Adams e-invariant with respect to KO-theory instead of KU (Adams 66, p. 39), which, in degrees $8k + 3$, is indeed half of the e-invariant $e_{\mathbb{C}}$ for $KU$ (by Adams 66, Prop. 7.14).

Diagrammatic construction

under construction – not complete yet

While the Adams e-invariant of a map exists when the its d-invariant vanishes, the classical constructions above implicitly proceed via a finer invariant of maps equipped with a trivialization of their d-invariant. In order to bring this out more explicitly, the following is meant to be another, more abstractly homotopy theoretic, way to approach the construction of the e-invariant (following SS21). This perspective turns out to make various properties immediately manifest, notably the equality between Adams’s construction via the Chern character on KU and Conner-Floyd’s construction via the Todd character on MUFr.

1. Preliminaries

2. Unit cofiber cohomology theory

3. The refined e-invariant

4. Recovering Adams’s construction

5. Recovering Conner-Floyd’s construction

Preliminaries

First some Notation:

• For $E$ a spectrum and $n \in \mathbb{Z}$ we write

  • $E^n \coloneqq \Omega^\infty \Sigma^n E$ for the $n$th component space

  • $E_n \coloneqq \pi_n(E) \simeq \widetilde E{}^0(S^n) \simeq \pi_0(E^{-n})$ for its homotopy groups.

• For $R$ a ring we write $H R$ for its Eilenberg-MacLane spectrum and $H^{\mathrm{ev}}R \;\coloneqq\; \underset{k \in \mathbb{N}}{\oplus} \Sigma^{2k} H R$ for its connective even 2-periodic version.

The Setup is as above, which we recall for completeness:

• Let $n, d \in \mathbb{N}$, with $d \geq 1$,

• consider a map $S^{2(n+d)-1} \xrightarrow{\;c\;} S^{2n}$ representing a class in $\mathbb{S}_{2d-1}$, which we will denote by the same name.

  Without restriction of generality we may assume that this class is non-trivial $c \neq 0 \,\in\, \mathbb{S}_{2d-1}\,.$

• We write $C_c$ for the cofiber space of $c$:

Unit cofiber cohomology theory

Definition

[Unit cofiber cohomology theory]

For $E$ a multiplicative cohomology theory (represented by a homotopy-commutative ring spectrum) with unit operation $\mathbb{S} \overset{ e^E }{\longrightarrow} E$ we denote the corresponding homotopy cofiber-theory $E/\mathbb{S}$.

(In notation common around the Adams spectral sequence this would be “$\Sigma \overline {E}$” – as in Adams 74, theorem 15.1 page 319 – or just “$\overline{ E }$” – as in Hopkins 99, Cor. 5.3).

Via the induced homotopy cofiber sequence

this comes with a canonical cohomology operation $\partial \;\colon\; E/\mathbb{S} \longrightarrow \Sigma \mathbb{S}$ to shifted stable Cohomotopy:

Definition

[Induced cohomology operations on cofiber cohomology] Let $E \overset{\phi}{\longrightarrow} F$ be a multiplicative cohomology operation, so that in particular it preserves the units, witnessed by a homotopy-commutative square on the left here: Then passing to homotopy cofibers yields the induced cohomology operation $\phi/\mathbb{S}$ on cofiber theories (Def. ).

Example

[Chern character on cofiber of K-theory] The Chern character operation $\mathrm{KU} \overset{\phi}{\longrightarrow} H^{\mathrm{ev}}\mathbb{Q}$ is multiplicative, hence passes to an operation $\mathrm{KU}/\mathbb{S} \overset{ \;\mathrm{ch}/\mathbb{S}\; }{\longrightarrow} H^{\mathrm{ev}}\mathbb{Q}$ via Def. .

In a similar fashion we get:

Remark

There is a canonical splitting $\mathrm{spl}_0$ of the short exact sequence

namely that coming from the inclusion $H\mathbb{Q} \hookrightarrow H^{\mathrm{ev}}\mathbb{Q}$ (which is multiplicative, in particular preserves the unit):

where on the left we used our assumption that $d \neq 0$.

We will use this canonical splitting together with the canonical splitting of the even rational cohomology of a cofiber space $S^{2(n+d)-1} \xrightarrow{ \;c\; } S^{2n} \xrightarrow{ \;\; } C_c$ given by the splitting into degrees $2(n+d)$ and $2n$

which is induced in the same fashion from the inclusion $H\mathbb{Q} \hookrightarrow H^{\mathrm{ev}}\mathbb{Q}$.

Both of these splittings are hence characterized by the fact that their corresponding retraction (see there) is projection onto rational cohomology in degree $2(n+d)$.

Lemma

(Cofiber $E$-cohomology as extension of stable Cohomotopy by $E$-cohomology)

For $E$ a multiplicative cohomology theory and $X$ a space, assume that the $E$-Boardman homomorphism $\widetilde {\mathbb{S}}{}^\bullet(X) \xrightarrow{ \;\beta^\bullet_X\; } \widetilde E^\bullet(X)$ is zero in degrees $n$ and $n + 1$ – for instance in that $X \simeq S^{k \geq 2}$, $n = 0$ and the groups $\widetilde E^0(S^k) = \pi_k(E)$ have no torsion – then the cohomology operations $i^E$, $\partial^E$ form a short exact sequence of cohomology groups:

(e.g. Stong 68, p. 102)

Proof

Generally, the long cofiber sequence of cohomology theories

induces a long exact sequence of cohomology groups (…)

Under the given assumption the two outermost morphisms shown are zero, and hence the sequence truncates as claimed.

The refined e-invariant

Proposition

Let $E$ be a multiplicative cohomology theory and $n,d \in \mathbb{N}$. Consider the function that sends pairs consisting of

1. the stable class $\big[ G^{\mathbb{S}}_n (c) \big]$ of a map $S^{n+d-1} \overset{\;c\;}{\longrightarrow} S^n$

2. the class of a trivialization $H^E_{n-1}\!(c)$ of its d-invariant in $E$-cohomology

to the class in $(E/\mathbb{S})_d$ of this diagram:

Then: This function respects the canonical fibrations of both sides over $\mathbb{S}_{d-1}$, i.e. it is a lift through the boundary map $\partial$.

See also this Prop. at d-invariant.

Proof

First, here is a quick formal argument to see that some such map does exist:

By Definition , an element in $H_{n-1}Fluxes^E\big( S^{n+d-1} \big)$ is equivalently the class of a homotopy cone with tip $\Sigma^{n+d-1} \mathbb{S}$ over the cospan formed by the ring spectrum unit $e^E$ and the zero morphism:

But in Spectra homotopy cofiber sequences are homotopy fiber sequences (by this Prop.), so that by the universal property of homotopy fibers the class of the above diagram induces the class of a map
$\vdash {\color{orange} H^E_{n-1}(c) } \;\colon\; \Sigma^{n+d-1}\mathbb{S} \longrightarrow fib\big( \Sigma^{n} e^E \big) \,\simeq\, \Sigma^{n-1} (E/\mathbb{S}$):

equipped with a homotopy from its image under $\partial$ to $c$.

This implies the claim, by

$$\pi_0 Maps \Big( \Sigma^{n+d - 1}\mathbb{S} \,,\, \Sigma^{n-1} (E/\mathbb{S}) \Big) \;\simeq\; (E/\mathbb{S})_{d} \,.$$

Second, to see that this map is realized as claimed (the following construction is close to the proof of Conner-Floyd 66, Theorem 16.2):

Let $\big[ S^{n + d - 1} \overset{c}{\longrightarrow} S^{n} \big] \;\in\; \pi^n\big(S^{n+d-1}\big)$ be a given class in Cohomotopy. We need to produce a map of the form

and show that it is a bijection onto this fiber, hence that the square is cartesian. To this end, we discuss the following homotopy pasting diagram, all of whose cells are homotopy cartesian:

For given $H^E_{n-1}\!(c)$, this diagram is constructed as follows (where we say “square” for any single cell and “rectangle” for the pasting composite of any adjacent pair of them):

• The two squares on the left are the stabilization of the homotopy pushout squares defining the cofiber space $C_c$ and the suspension of $S^{n + d - 1}$

• The bottom left rectangle (with $\Sigma^n(e^E)$ at its top) is the homotopy pushout defining $\Sigma^n(E\!/\mathbb{S})$.

• The classifying map for the given $(n-1)$-flux, shown as a dashed arrow, completes a co-cone under the bottom left square. Thus the map ${\color{magenta}M^d}$ forming the bottom middle square is uniquely implied by the homotopy pushout property of the bottom left square. Moreover, the pasting law implies that this bottom middle square is itself homotopy cartesian.

• The bottom right square is the homotopy pushout defining $\partial$.

• By the pasting law it follows that also the bottom right rectangle is homotopy cocartesian, hence that, after the two squares on the left, it exhibits the third step in the long homotopy cofiber sequence of $\Sigma^\infty c$. This means that its total bottom morphism is $\Sigma^{\infty + 1} c$, and hence that $\partial \big[ M^d \big] = [c]$.

In conclusion, these construction steps yield a map $H^E_{n-1}\!(c) \mapsto M^d$ over $[\Sigma^\infty c]$, as required.

Definition

The refined e-invariant $\widehat e_{KU}$ is the composite of

1. the equivalence from Prop. for $E =$ KU,

2. the cofiber Chern character from Example ,

3. the canonical splitting from Remark :

sending a trivialization of the d-invariant

to the class of this pasting composite:

Lemma

The values of the refined e-invariant from Def. for fixed Cohomotopy class $[c]$ form an integer lattice inside the rational numbers:

$$\widehat e_{\mathrm{KU}} \Big( [c], \big[ H^{\mathrm{KU}}_{2d-1}\!(c) \big] \Big) - \widehat e_{\mathrm{KU}} \Big( [c], \big[ {H}^\prime{}^{\mathrm{KU}}_{2d-1}\!(c) \big] \Big) \;\in\; \mathbb{Z}$$

Proof

Using the same three ingredients that enter Def. , we paste together the following commuting diagram, whose vertical middle composite is the refined $\widehat e_{KU}$-invariant:

Now observe that:

1. by Lemma the middle rows of this diagram are exact;

2. the left vertical map is the canonical injection, since the Chern character is multiplicative, and in particular respects the unit.

By (1) the difference between any two choices of trivializations of the d-invariant (of $H^E_{n-1}$-fluxes) is an integer in the top left, and by (2) this translates to an integer difference between their $\widehat e$-invariants as we pass to the bottom of the diagram.

Hence we have a diagrammatic construction of an invariant of $[c]$ in $\mathbb{Q}/\mathbb{Z}$. It just remains to see that this actually coincides with the classical Adams invariant:

Recovering Adams’s construction

Remark

Observe that both the classical Adams invariant and diagrammatic construction from Def. above extract a rational number via a canonical splitting in both cases retracting onto rational cohomology $\simeq \mathbb{Q}$ in degree $2(n+d)$ (Remark ).

For the classical Adams invariant this is the content of Prop. , which we may summarize more succinctly:

Therefore we check that these two canonical splittings are compatible:

Lemma

Given non-trivial $\big[ S^{2(n+d)-1} \xrightarrow{\;c\;} S^{2n}\big] \,\in \, \mathbb{S}_{2d-1}$ for any $n,d \in \mathbb{N}$ with $d \geq 1$, we have a commuting diagram of the following form:

Here:

• The rear morphisms are pushforward along the projection $E \xrightarrow{i} E/\mathbb{S}$
  and pullback along $C_c \xrightarrow{p} S^{2(n+d)}$, respectively;

• $\mathrm{spl}_0$ denotes the canonical isomorphisms from Remark ;

• $\mathbb{S}_{2d-1}/\mathbb{Z}$ denotes the cofiber of $\mathbb{Z} \xrightarrow{\;c\;} \mathbb{S}_{2d-c}$;

• the symbol $\oplus'$ denotes some possibly non-trivial extension, left undetermined, of Q/Z by $\mathbb{S}_{d-1}/\mathbb{Z}$, and vice versa;

• the matrices act as usual, on row vectors by matrix multiplication from the right.

Proof

Consider the diagram which is the image under $\pi_0 \mathrm{Maps}^{\ast/}(-,-)$ of the sequences

In this diagram all rows and columns are long exact sequences of generalized cohomology groups (since $\mathrm{Maps}^{\ast/}$ sends both homotopy cofiber sequences in the first argument as well as homotopy fiber sequences in the second argument to homotopy fiber sequences, and using that these induce long exact sequences of homotopy groups).

By the definition (or characterization) of reduced generalized cohomology groups, this diagram is equal (in the sector shown) to the following commuting diagram of abelian groups:

Evaluating here all the cohomology groups on spheres yields:

Now recognizing split exact sequences using the vanishing Ext-groups $Ext^1(-,\mathbb{Q}) = 0$ and $Ext^1(\mathbb{Z},-) = 0$ (see here) yields:

Here the two identifications shown in magenta we may choose to be the canonical ones from Remark .

From this, and using again $\mathrm{Ext}^1(-,\mathbb{Q}) = 0$ together with $\mathrm{Ext}^1(-, A \oplus B ) \simeq \mathrm{Ext}^1(-,A) \oplus \mathrm{Ext}^1(-,B)$ (by this Prop.), the remaining entry and the maps into it must be as claimed:

Theorem

The diagrammatic $\widehat e_{\mathrm{KU}}$-invariant from Def. reproduces the classical Adams $e_{\mathbb{C}}$-invariant.

Proof

The homotopy-commuting rectangle in the bottom right part of the defining pasting diagram Def. says that

$$p^\ast \Big( \widehat e_{\mathrm{KU}}(c) , [c] \Big) \;=\; i_\ast \Big( \mathrm{ch} \big[ \vdash H^{\mathrm{KU}}_{2n-1}(c) \big] \Big) \,.$$

By Lemma this means that the image of both sides along their canonical retractions (Remark ) onto degree=$2(n+d)$ rational cohomology $\simeq \mathbb{Q}$ coincide. But by Definition and Remark , this is the claimed equality (even at the level of refined invariants, i.e. before forgetting choices of trivializations of the d-invaariant, hence before quotienting by $\mathbb{Q}$).

Recovering Conner-Floyd’s e-invariant

With this diagrammatic formulation of the e-invariant, the Conner-Floyd theorem – that the e-invariant is the Todd class of cobounding (U,fr)-manifolds – follows as an immediate corollary: It just amounts to factoring the above pasting composite further through MU, as follows:

using that the rational Todd class is the Chern character of the Thom class and that this identification is represented by a corresponding factorization of maps of multiplicative cohomology theories, as shown (e.g. Smith 73, Section 1)

Examples

Third stable homotopy group of spheres

Proposition

(Adams 66, Example 7.17 and p. 46)

In degree 3, the KO-theoretic e-invariant $e_{\mathbb{R}}$ takes the value $\left[\tfrac{1}{24}\right] \in \mathbb{Q}/\mathbb{Z}$ on the quaternionic Hopf fibration $S^7 \overset{h_{\mathbb{H}}}{\longrightarrow} S^4$ and hence reflects the full third stable homotopy group of spheres:

$$\array{ \pi^s_3 & \underoverset{ \simeq }{ e_{\mathbb{R}} }{ \;\;\longrightarrow\;\; } & \mathbb{Z}/24 & \subset & \mathbb{Q}/\mathbb{Z} \\ [h_{\mathbb{H}}] &&\mapsto&& \left[\tfrac{1}{24}\right] }$$

while $e_{\mathbb{C}}$ sees only “half” of it (by Adams 66, Prop. 7.14).

Related concepts

• eta-invariant

• d-invariant, f-invariant

• Hopf invariant, Hopf invariant one problem

• J-homomorphism

• stable homotopy groups of spheres

References

The definition is due to:

• John Adams, Sections 3,7 of: On the groups $J(X)$ IV, Topology 5: 21 (1966) (pdf, doi:10.1016/0040-9383(66)90004-8)

  Correction, Topology 7 (3): 331 (1968)

Discussion in more general Whitehead generalized cohomology theories:

• Warren M. Krueger, Generalized Steenrod-Hopf Invariants for Stable Homotopy Theory, Proceedings of the American Mathematical Society, Vol. 39, No. 3 (Aug., 1973), pp. 609-615 (jstor:2039603)

• Warren M. Krueger, Relation with the Hopf invariant revisited, Illinois J. Math. Volume 24, Issue 2 (1980), 188-191 (euclid:ijm/1256047713)

and in relation to the Adams spectral sequence:

• Robert Switzer, Section 19.19 in: Algebraic Topology - Homotopy and Homology, Grundlehren der Mathematischen Wissenschaften, Vol. 212, Springer, 1975 (doi:10.1007/978-3-642-61923-6)

and to the f-invariant:

• Mark Behrens, Gerd Laures, $\beta$-Family congruences and the $f$-invariant, Geometry & Topology Monographs 16 (2009) 9–29 (arXiv:0809.1125, doi: 10.2140/gtm.2009.16.9)

Interpretation in MUFr bordism theory:

• Pierre Conner, Edwin Floyd, Section 16 of: The Relation of Cobordism to K-Theories, Lecture Notes in Mathematics 28, Springer 1966 (doi:10.1007/BFb0071091, MR216511)

Interpretation via index theory:

• Michael Atiyah, Vijay Patodi, Isadore Singer, p. 18 onwards in: Spectral asymmetry and Riemannian geometry. II, Volume 78, Issue 3 November 1975 , pp. 405-432 (doi:10.1017/S0305004100051872)

Review and exposition:

• Charles Weibel, chapter VI, section 2 of The K-book (pdf)

• Ulrich Bunke, Section 2 of: Differential cohomology in geometry and analysis, talk 2008 (pdf, pdf)

• Klaus Wirthmüller, p. 52 (54 of 67) in: Vector bundles and K-theory, 2012 (pdf)

• Michael Hopkins (notes by Akhil Mathew), Lecture 11 in: Spectra and stable homotopy theory, 2012 (pdf, pdf)

• Gereon Quick, The $e$-invariant, lecture notes in: Advanced algebraic topology, 2014 (pdf)

• Gereon Quick, The $e$-invariant and the $J$-homomorphism, lecture notes in: Advanced algebraic topology, 2014 (pdf)

Discussion via Toda brackets:

• Hiroaki Hamanaka, Adams $e$-invariant, Toda bracket and $[X, U(n)]$, J. Math. Kyoto Univ. Volume 43, Number 4 (2003), 815-827. (euclid:kjm/1250281737)

Discussion in MU-theory:

• N. V. Panov, Characteristic numbers in $U$-theory, Akad. Nauk SSSR Ser. Mat., 1971 Volume 35, Issue 6 (mathnet:2174)

Discussion in BP-theory:

• Yasumasa Hirashima, On the $BP_\ast$-Hopf invariant, Osaka J. Math., Volume 12, Number 1 (1975), 187-196 (euclid:ojm/1200757733)

• Martin Bendersky, The BP Hopf Invariant, American Journal of Mathematics, Vol. 108, No. 5 (Oct., 1986) (jstor:2374595)