nLab Dirac charge quantization

Idea

For monopole charges in electromagnetism

If the field of electromagnetism serves as a background gauge field for electrically charged quantum particles it is subject to a quantization condition: Outside the locus of any magnetic charge – for instance a magnetic monopole topological defect – the electromagnetic field must be a connection on a principal U(1) bundle whose first Chern class is the discrete measure for the units of magnetic charge. Equivalently this means that the electromagnetic field is a cocycle in ordinary differential cohomology of degree 2.

In the underlying topological sector (“monopole”/“instantons”-sector) this is integral cohomology in degree-2, whose classifying space is equivalently the infinite complex projective space $B U(1) \simeq \mathbb{C}P^\infty$:

$\,$

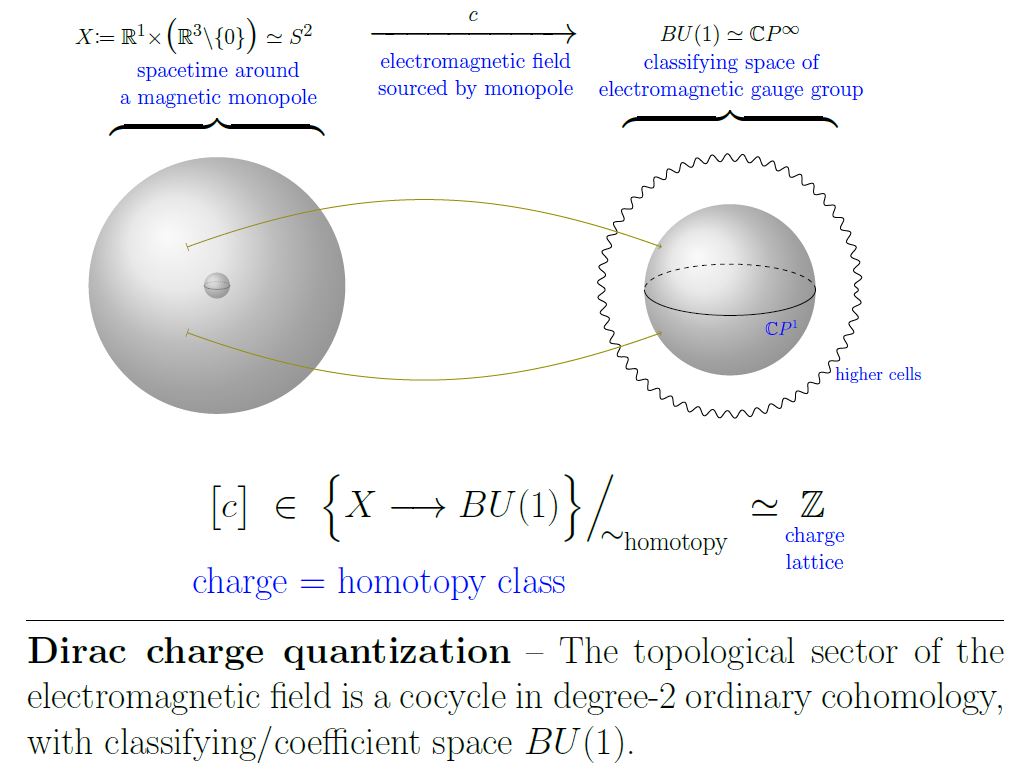
This goes back to an insight due to Dirac 31. See Heras 18 for traditional elementary review, but see Alvarez 85, Frankel and Mangiarotti-Sardanashvily 00 for exposition of the modern picture in terms of fiber bundles in physics. See Freed 00, Section 2 for review in terms of differential cohomology with outlook to generalization to higher gauge fields in string theory (more on which in the references below).

A closely related phenomenon is the magnetic flux quantization in type II superconductors, see there.

On the locus of the magnetic charge itself the situation is more complex. There the magnetic current is given by a cocycle in ordinary differential cohomology of degree 3 (with compact support) and now the electromagnetic field is a connection on a twisted bundle (Freed 00, Section 2).

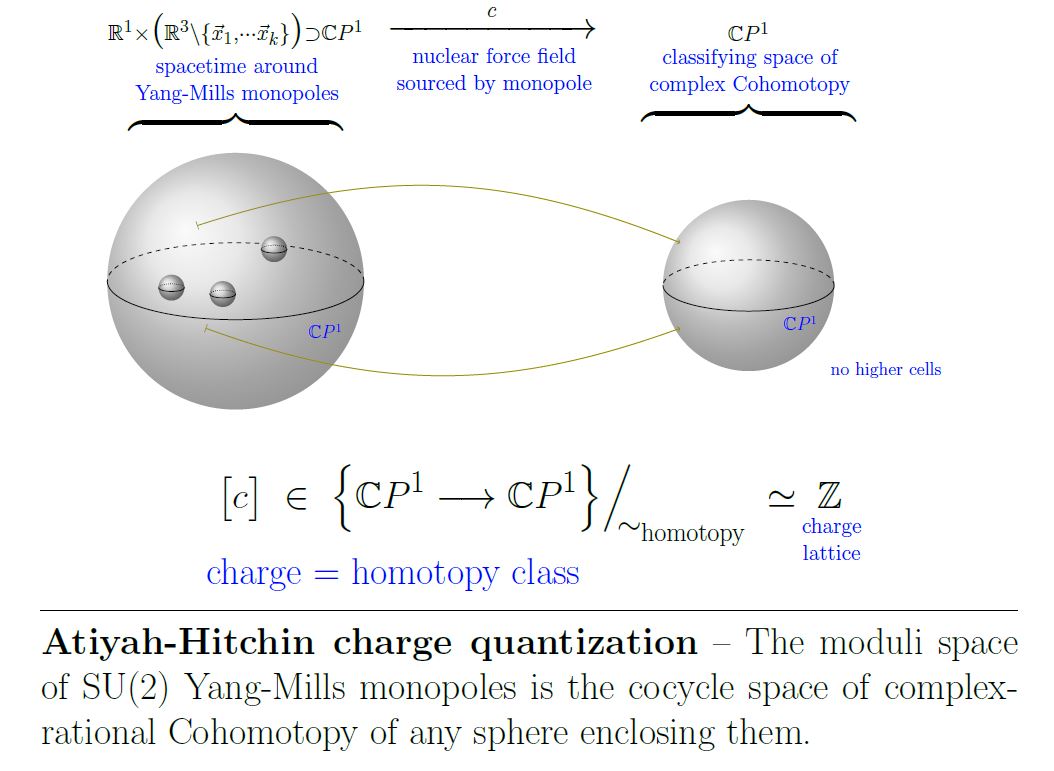
For monopole charges in non-abelian Yang-Mills theory

A similar charge quantization condition govers monopoles in SU(2)-Yang-Mills theory, see at moduli space of monopoles. Here the Atiyah-Hitchin charge quantization (Atiyah-Hitchin 88, Theorem 2.10) says that the moduli space of monopoles is the complex-rational 2-Cohomotopy of an asymptotic 2-sphere enclosing the monopoles:

$\,$

For RR-field D-brane charges in K-theory

See at D-brane charge quantization in K-theory

For the C-field in J-twisted Cohomotopy

See at supergravity C-field – shifted flux quantization condition

Related entries

• flux, flux tube, flux compactification, uncertainty of fluxes

• geometry of physics – flux quantization

• fiber bundles in physics

• non-perturbative quantum field theory

• monopole

  • Dirac monopole, Yang monopole

• moduli space of monopoles

References

See also the references at fiber bundles in physics.

For the electromagnetic field

The original argument for charge quantization of the electromagnetic field:

• P.A.M. Dirac, Quantized Singularities in the Electromagnetic Field, Proceedings of the Royal Society A 133 (1931) 60-72 [doi:10.1098/rspa.1931.0130]

Further early discussion

• Julian Schwinger, Magnetic Charge and Quantum Field Theory, Phys. Rev. 144 (1966) 1087 [doi:10.1103/PhysRev.144.1087]

• Daniel Zwanziger, Quantum Field Theory of Particles with Both Electric and Magnetic Charges, Phys. Rev. 176 (1968) 1489 [doi:10.1103/PhysRev.176.1489]

Understanding of charge quantization in terms of Čech cohomology:

• Orlando Alvarez, Cohomology and Field Theory, talk at: Symposium on Anomalies, Geometry, Topology, Argonne IL (28-30 March 1985) [inspire:965785, pdf, pdf]

• Orlando Alvarez, Topological quantization and cohomology, Comm. Math. Phys. 100 2 (1985) 279-309 [euclid:cmp/1103943448]

reviewed in:

• Guillermo A. González, Cohomologa de Cĕch y Cuantización Topológica de Parámetros Físicos, Revista de la Academia Colombiana de Ciencias Exactas, Físicas y Naturales 47 182 (2023) 51-71 [doi:10.18257/raccefyn.1782, pdf]

General review and further discussion:

• Jean-Luc Brylinski, §7.1 in: Loop spaces, characteristic classes and geometric quantization, Birkhäuser (1993) [doi:10.1007/978-0-8176-4731-5]

• Theodore Frankel, section 16.4e of: The Geometry of Physics - An Introduction, Cambridge University Press (1997, 2004, 2012) [doi:10.1017/CBO9781139061377]

• Luis Alvarez-Gaumé, Frederic Zamora, Section II in: Duality in Quantum Field Theory (and String Theory), AIP Conference Proceedings 423 (1998) 46–83 [arXiv:hep-th/9709180, doi:10.1063/1.55087]

• Daniel Freed, Section 2 of: Dirac charge quantization and generalized differential cohomology, Surveys in Differential Geometry 7, Int. Press (2000) 129-194 [arXiv:hep-th/0011220, doi:10.4310/SDG.2002.v7.n1.a6, spire:537392]

• L. Mangiarotti, Gennadi Sardanashvily, Connections in Classical and Quantum Field Theory, World Scientific, 2000 (doi:10.1142/2524)

• Yakov Shnir, Section 2.1 of: Magnetic Monopoles, Springer 2005 (ISBN:978-3-540-29082-7)

• Freed, Moore & Segal 2007, p. 7

• Ricardo Heras, Dirac quantisation condition: a comprehensive review, Contemp. Phys. 59, 331 (2018) (arXiv:1810.13403)

See also

• Wikipedia, Dirac’s quantization

Arguments for electric charge quantization from anomaly cancellation in the standard model of particle physics:

• K. S. Babu and Rabindra N. Mohapatra, Quantization of electric charge from anomaly constraints and a Majorana neutrino, Phys. Rev. D 41 (1990) 271 [doi:10.1103/PhysRevD.41.271]

Consideration of combined magnetic and electric charge quantization in vacuum (cf. duality-symmetric electromagnetism):

• Daniel S. Freed, Gregory W. Moore, Graeme Segal, The Uncertainty of Fluxes, Commun. Math. Phys. 271 (2007) 247-274 [arXiv:hep-th/0605198, doi:10.1007/s00220-006-0181-3]

• Christian Becker, Marco Benini, Alexander Schenkel, Richard Szabo, Rem. 2.3 in: Abelian duality on globally hyperbolic spacetimes, Commun. Math. Phys. 349 (2017) 361-392 [arXiv:1511.00316, doi:10.1007/s00220-016-2669-9]

• Calin Lazaroiu, Carlos S. Shahbazi, around Def. 1.16 in: The duality covariant geometry and DSZ quantization of abelian gauge theory, Advances in Theoretical and Mathematical Physics 26 (2022) 2213–2312 [arXiv:2101.07236, doi:10.4310/ATMP.2022.v26.n7.a5]

• Calin Lazaroiu, Carlos S. Shahbazi, around (3) in: The geometry and DSZ quantization of four-dimensional supergravity, Letters in Mathematical Physics 113 4 (2023) [arXiv:2101.07778, doi:10.1007/s11005-022-01626-y]

For the weak nuclear force field

Discussion of the moduli space of monopoles for SU(2)-Yang-Mills theory (weak nuclear force):

• Michael Atiyah, Nigel Hitchin, The geometry and dynamics of magnetic monopoles M. B. Porter Lectures. Princeton University Press, Princeton, NJ, 1988 (jstor:j.ctt7zv206)

• Graeme Segal, The topology of spaces of rational functions, Acta Math. Volume 143 (1979), 39-72 (euclid:1485890033)

D-brane charge quantization in ordinary cohomology

Discussion of charge quantization of D-branes in (relative) ordinary cohomology:

• José Figueroa-O’Farrill, Sonia Stanciu, D-brane charge, flux quantisation and relative (co)homology, JHEP 0101 (2001) 006 [arXiv:hep-th/0008038, doi:10.1088/1126-6708/2001/01/006]

• Kazuya Yonekura, Constraints on the topology of Type IIB string theory [arXiv:2403.04127, InSpire:2767009]

D-brane charge quantization in topological K-theory

On the conjectural D-brane charge quantization in topological K-theory:

Origin and basics

The idea that D-branes have Dirac charge quantization in topological K-theory originates with the observation that their charge expressed in RR-field flux densities resembles the image of a Chern character:

• Michael Green, Jeffrey A. Harvey, Gregory Moore, I-Brane Inflow and Anomalous Couplings on D-Branes, Class. Quant. Grav. 14 (1997) 47-52 [doi:10.1088/0264-9381/14/1/008, arXiv:hep-th/9605033]

• Ruben Minasian, Gregory Moore, K-theory and Ramond-Ramond charge, JHEP 9711:002 (1997) [doi:10.1088/1126-6708/1997/11/002, arXiv:hep-th/9710230]

Further early discussion:

• Edward Witten, D-Branes And K-Theory, JHEP 9812:019 (1998) [arXiv:hep-th/9810188, doi:10.1088/1126-6708/1998/12/019]

• Petr Hořava, Type IIA D-Branes, K-Theory, and Matrix Theory (1998). (hep-th/9812135).

• Daniel Freed, Michael Hopkins, On Ramond-Ramond fields and K-theory, JHEP 0005 (2000) 044 [doi:10.1088/1126-6708/2000/05/044, arXiv:hep-th/0002027]

and with emphasis on the full picture of twisted differential K-theory in:

• Daniel Freed, Dirac charge quantization and generalized differential cohomology, Surveys in Differential Geometry, Int. Press, Somerville, MA, 2000, pp. 129–194 (arXiv:hep-th/0011220, doi:10.4310/SDG.2002.v7.n1.a6, spire:537392)

Here:

• Green, Harvey & Moore (1997), Minasian & Moore (1997) observe that RR-field flux form-expressions for D-brane charge look like images of K-theory classes under the Chern character;

From Sch 18

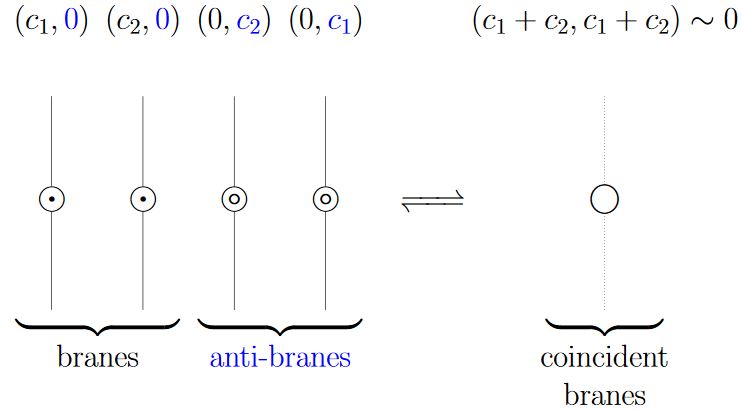
• Witten 98, Section 3 adds the observation that the tachyon condensation – which is expected (this is Sen's conjecture from Sen 98) for open strings between D-brane/anti-D-branes – plausibly implements on their Chan-Paton vector bundles the defining equivalence relation (here) of topological K-theory.

Expression of these D-brane K-theory classes via the Atiyah-Hirzebruch spectral sequence:

• Juan Maldacena, Gregory Moore, Nathan Seiberg, D-Brane Instantons and K-Theory Charges, JHEP 0111:062,2001 (arXiv:hep-th/0108100)

• Jarah Evslin, Hisham Sati, Can D-Branes Wrap Nonrepresentable Cycles?, JHEP0610:050,2006 (arXiv:hep-th/0607045)

Specifically for D-branes in WZW models see

• Peter Bouwknegt, A note on equality of algebraic and geometric D-brane charges in WZW models (pdf)

Understanding the solitonic (non-singular) D-branes and their T-duality in K-theory:

• Oren Bergman, Eric G. Gimon, Petr Hořava, Brane Transfer Operations and T-Duality of Non-BPS States, JHEP 9904 (1999) 010 [doi:10.1088/1126-6708/1999/04/010, arXiv:hep-th/9902160]

Towards a matrix model taking these K-theoretic effects into account (K-matrix model):

• Tsuguhiko Asakawa, Shigeki Sugimoto, Seiji Terashima, D-branes, Matrix Theory and K-homology, JHEP 0203 (2002) 034 [doi:10.1088/1126-6708/2002/03/034, arXiv:hep-th/0108085]

Twisted, equivariant and differential refinement

Discussion of charge quantization in twisted K-theory for the case of non-vanishing B-field:

• Witten 98, Sec. 5.3 (for torsion twists)

• Peter Bouwknegt, Varghese Mathai, D-branes, B-fields and twisted K-theory, Int. J. Mod. Phys. A 16 (2001) 693-706 [doi:10.1088/1126-6708/2000/03/007, arXiv:hep-th/0002023]

An elaborate proposal for the correct flavour of equivariant KR-theory needed for orientifolds is sketched in:

• Jacques Distler, Dan Freed, Greg Moore, Orientifold Précis in: Hisham Sati, Urs Schreiber (eds.) Mathematical Foundations of Quantum Field and Perturbative String Theory Proceedings of Symposia in Pure Mathematics, AMS (2011) (arXiv:0906.0795, slides)

Discussion of full-blown twisted differential K-theory and its relation to D-brane charge in type II string theory

• Daniel Grady, Hisham Sati, Ramond-Ramond fields and twisted differential K-theory, Advances in Theoretical and Mathematical Physics 26 5 (2022) [doi:10.4310/ATMP.2022.v26.n5.a2, arXiv:1903.08843]

Discussion of full-blown twisted differential orthogonal K-theory and its relation to D-brane charge in type I string theory (on orientifolds):

• Daniel Grady, Hisham Sati, Twisted differential KO-theory (arXiv:1905.09085)

Reviews

• Kasper Olsen, Richard Szabo, Brane Descent Relations in K-theory, Nucl.Phys. B566 (2000) 562-598 (arXiv:hep-th/9904153)

• Kasper Olsen, Richard Szabo, Constructing D-Branes from K-Theory, Adv. Theor. Math. Phys. 3 (1999) 889-1025 (arXiv:hep-th/9907140)

• John Schwarz, TASI Lectures on Non-BPS D-Brane Systems (arXiv:hep-th/9908144)

• Edward Witten, Overview Of K-Theory Applied To Strings, Int. J. Mod. Phys. A16:693-706, 2001 (arXiv:hep-th/0007175)

• Greg Moore, K-Theory from a physical perspective, in: Ulrike Tillmann (ed.) Topology, Geometry and Quantum Field Theory, Proceedings of the 2002 Oxford Symposium in Honour of the 60th Birthday of Graeme Segal, Cambridge University Press (2004) (arXiv:hep-th/0304018, doi:10.1017/CBO9780511526398.011)

• Juan José Manjarín, Topics on D-brane charges with B-fields, Int. J. Geom. Meth. Mod. Phys. 1 (2004) (arXiv:hep-th/0405074)

• Jarah Evslin, What Does(n’t) K-theory Classify?, Modave Summer School in Mathematical Physics (arXiv:hep-th/0610328, spire:730502)

• Stefan Fredenhagen, Physical Background to the K-Theory Classification of D-Branes: Introduction and References (doi:10.1007/978-3-540-74956-1_1), chapter in: Dale Husemoeller, Michael Joachim, Branislav Jurčo, Martin Schottenloher, Basic Bundle Theory and K-Cohomology Invariants, Lecture Notes in Physics, Springer (2008) 1-9 [doi:10.1007/978-3-540-74956-1, pdf]

• Fabio Ruffino, Topics on topology and superstring theory (arXiv:0910.4524)

• Hisham Sati, Urs Schreiber: Flux Quantization, in Encyclopedia of Mathematical Physics 2nd ed, Elsevier (2024) [arXiv:2402.18473]

Amplification of torsion-charges implied by charge quantization in Ktheory

• Volker Braun, K-Theory Torsion [arXiv:hep-th/0005103]

• Ilka Brunner, Jacques Distler, Torsion D-Branes in Nongeometrical Phases, Adv. Theor. Math. Phys. 5 (2002) 265-309 [doi:10.4310/ATMP.2001.v5.n2.a3, arXiv:hep-th/0102018]

• Ilka Brunner, Jacques Distler, Rahul Mahajan, Return of the Torsion D-Branes, Adv. Theor. Math. Phys. 5 (2002) 311-352 [doi:10.4310/ATMP.2001.v5.n2.a4, arXiv:hep-th/0106262]

Review of D-branes charge seen in KK-theory:

• Richard Szabo, D-branes and bivariant K-theory, Noncommutative Geometry and Physics 3 1 (2013): 131. (arXiv:0809.3029)

based on

• Rui Reis, Richard Szabo, Geometric K-Homology of Flat D-Branes , Commun. Math. Phys. 266 (2006) 71-122 [arXiv:hep-th/0507043]

• Jacek Brodzki, Varghese Mathai, Jonathan Rosenberg, Richard Szabo, D-Branes, RR-Fields and Duality on Noncommutative Manifolds, Commun. Math. Phys. 277 (2008) 643-706 [doi:10.1007/s00220-007-0396-y, arXiv:hep-th/0607020]

• Jacek Brodzki, Varghese Mathai, Jonathan Rosenberg, Richard Szabo, Noncommutative correspondences, duality and D-branes in bivariant K-theory, Adv. Theor. Math. Phys. 13:497-552, 2009 (arXiv:0708.2648)

• Jacek Brodzki, Varghese Mathai, Jonathan Rosenberg, Richard Szabo, D-branes, KK-theory and duality on noncommutative spaces, J. Phys. Conf. Ser. 103 012004 (2008) [doi:10.1088/1742-6596/103/1/012004, arXiv:0709.2128]

In particular (BMRS2) discusses the definition and construction of D-brane charge as a generalized index in KK-theory. The discussion there focuses on the untwisted case. Comments on the generalization of this to topologicall non-trivial B-field and hence twisted K-theory is in

• Richard Szabo, D-Branes, Tachyons and K-Homology, Mod. Phys. Lett. A17 (2002) 2297-2316 (arXiv:hep-th/0209210)

Conceptual problems

But there remain conceptual issues with the proposal that D-brane charge is in K-theory, as highlighted in

• Jan de Boer, Robbert Dijkgraaf, Kentaro Hori, Arjan Keurentjes, John Morgan, David Morrison, Savdeep Sethi, section 4.5.2 and 4.6.5 of Triples, Fluxes, and Strings, Adv. Theor. Math. Phys. 4 (2002) 995-1186 [arXiv:hep-th/0103170, pdf]

• Jarah Evslin, section 8 of: What Does(n’t) K-theory Classify?, Second Modave Summer School in Mathematical Physics [arXiv:hep-th/0610328]

In particular, actual checks of the proposal that D-brane charge is given by K-theory, via concrete computation in boundary conformal field theory, have revealed some subtleties:

• Stefan Fredenhagen, Thomas Quella, Generalised permutation branes, JHEP 0511:004 (2005) [arXiv:hep-th/0509153, doi:10.1088/1126-6708/2005/11/004]

  It might surprise that despite all the progress that has been made in understanding branes on group manifolds, there are usually not enough D-branes known to explain the whole charge group predicted by (twisted) K-theory. […] it is fair to say that a satisfactory answer is still missing.

The closest available towards an actual check of the argument for K-theory via open superstring tachyon condensation (Witten 98, Section 3) seems to be

• Theodore Erler, Analytic Solution for Tachyon Condensation in Berkovits’ Open Superstring Field Theory, JHEP 1311 (2013) 007 [doi:10.1007/JHEP11(2013)007, arXiv:1308.4400]

which, however, concludes (on p. 32) with:

It would also be interesting to see if these developments can shed light on the long-speculated relation between string field theory and the K-theoretic description of D-brane charge $[$75, 76, 77]. We leave these questions for future work.

See also

• Theodore Erler, Four Lectures on Analytic Solutions in Open String Field Theory (arXiv:1912.00521, spire:1768105)

which still lists (on p. 112) among open problems of string field theory:

“Are there topological invariants of the open string star algebra representing D-brane charges?”

For orbifolds in equivariant K-theory

The proposal that D-brane charge on orbifolds is measured in equivariant K-theory (orbifold K-theory) goes back to

• Witten 98, section 5.1

It was pointed out that only a subgroup of equivariant K-theory can be physically relevant in

• Jan de Boer, Robbert Dijkgraaf, Kentaro Hori, Arjan Keurentjes, John Morgan, David Morrison, Savdeep Sethi, around (137) of: Triples, Fluxes, and Strings, Adv.Theor.Math.Phys. 4 (2002) 995-1186 (arXiv:hep-th/0103170)

Further discussion of equivariant K-theory for D-branes on orbifolds includes the following:

• Hugo García-Compeán, D-branes in orbifold singularities and equivariant K-theory, Nucl.Phys. B557 (1999) 480-504 (arXiv:hep-th/9812226)

• Matthias Gaberdiel, Bogdan Stefanski, Dirichlet Branes on Orbifolds, Nucl.Phys.B578:58-84, 2000 (arXiv:hep-th/9910109)

• Igor Kriz, Leopoldo A. Pando Zayas, Norma Quiroz, Comments on D-branes on Orbifolds and K-theory, Int. J. Mod. Phys. A 23 (2008) 933-974 [arXiv:hep-th/0703122]

• Richard Szabo, Alessandro Valentino, Ramond-Ramond Fields, Fractional Branes and Orbifold Differential K-Theory, Commun.Math.Phys.294:647-702, 2010 (arXiv:0710.2773)

Discussion of real K-theory for D-branes on orientifolds includes the following:

The original observation that D-brane charge for orientifolds should be in KR-theory is due to

• Witten 98, section 5

and was then re-amplified in

• Sergei Gukov, K-Theory, Reality, and Orientifolds, Commun.Math.Phys. 210 (2000) 621-639 (arXiv:hep-th/9901042)

• Oren Bergman, E. Gimon, Shigeki Sugimoto, Orientifolds, RR Torsion, and K-theory, JHEP 0105:047, 2001 (arXiv:hep-th/0103183)

With further developments in

• Varghese Mathai, Michael Murray, Daniel Stevenson, Type I D-branes in an H-flux and twisted KO-theory, JHEP 0311 (2003) 053 (arXiv:hep-th/0310164)

Discussion of orbi-orienti-folds using equivariant KO-theory is in

• N. Quiroz, Bogdan Stefanski, Dirichlet Branes on Orientifolds, Phys.Rev. D66 (2002) 026002 (arXiv:hep-th/0110041)

• Volker Braun, Bogdan Stefanski, Orientifolds and K-theory (arXiv:hep-th/0206158)

• H. Garcia-Compean, W. Herrera-Suarez, B. A. Itza-Ortiz, O. Loaiza-Brito, D-Branes in Orientifolds and Orbifolds and Kasparov KK-Theory, JHEP 0812:007, 2008 (arXiv:0809.4238)

Discussion of the alleged K-theory classification of D-brane charge in relation to the M-theory C-field is in

• Duiliu-Emanuel Diaconescu, Gregory Moore, Edward Witten, $E_8$ Gauge Theory, and a Derivation of K-Theory from M-Theory, Adv.Theor.Math.Phys.6:1031-1134,2003 (arXiv:hep-th/0005090), summarised in A Derivation of K-Theory from M-Theory (arXiv:hep-th/0005091)

See also

• Inaki Garcia-Etxebarria, Angel Uranga, From F/M-theory to K-theory and back, JHEP 0602:008,2006 (arXiv:hep-th/0510073)

More complete discussion of double dimensional reduction of the supergravity C-field in 11d to the expected B-field and RR-field flux forms in 10d:

• Varghese Mathai, Hisham Sati, Some Relations between Twisted K-theory and $E_8$ Gauge Theory, JHEP0403:016,2004 (arXiv:hep-th/0312033)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Rational sphere valued supercocycles in M-theory and type IIA string theory, Journal of Geometry and Physics, Volume 114, Pages 91-108 April 2017 (arXiv:1606.03206, doi:10.1016/j.geomphys.2016.11.024)

For the C-field in F-theory

Discussion of shifted C-field flux quantization of the C-field in F-theory:

• Andres Collinucci, Raffaele Savelli, On Flux Quantization in F-Theory, J. High Energ. Phys. 2012 15 (2012) [arXiv:1011.6388, doi:10.1007/JHEP02(2012)015]

• Andres Collinucci, Raffaele Savelli, On Flux Quantization in F-Theory II: Unitary and Symplectic Gauge Groups, J. High Energ. Phys. 2012 94 (2012) [arXiv:1203.4542, doi:10.1007/JHEP08(2012)094]

• Raffaele Savelli, Flux Quantization in F-theory and Freed-Witten anomaly, talk at StringMath (2012) [pdf, pdf]

For the C-field in M-theory

Discussion of shifted C-field flux quantization of the C-field in D=11 supergravity/M-theory:

• E. Diaconescu, Dan Freed, Greg Moore, The $M$-theory 3-form and $E_8$-gauge theory, chapter in Haynes Miller, Douglas Ravenel (eds.) Elliptic Cohomology Geometry, Applications, and Higher Chromatic Analogues, Cambridge University Press 2007 (arXiv:hep-th/0312069, doi:10.1017/CBO9780511721489)

• Dan Freed, Greg Moore, Setting the quantum integrand of M-theory, Communications in Mathematical Physics, Volume 263, Number 1, 89-132, (arXiv:hep-th/0409135, doi:10.1007/s00220-005-1482-7)

• Greg Moore, Anomalies, Gauss laws, and Page charges in M-theory (arXiv:hep-th/0409158)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, The moduli 3-stack of the C-field, Communications in Mathematical Physics, Volume 333, Issue 1 (2015), Page 117-151, (arXiv:1202.2455, DOI 10.1007/s00220-014-2228-1)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, M5-branes, String 2-connections, and 7d nonabelian Chern-Simons theory Advances in Theoretical and Mathematical Physics, Volume 18, Number 2 (2014) p. 229?321 (arXiv:1201.5277, doi:10.4310/ATMP.2014.v18.n2.a1)

Discussion in twisted Cohomotopy (“Hypothesis H”):

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Twisted Cohomotopy implies M-theory anomaly cancellation (arXiv:1904.10207)

• Domenico Fiorenza, Hisham Sati, Urs Schreiber, Twisted Cohomotopy implies M5 WZ term level quantization (arXiv:1906.07417)

and in equivariant Cohomotopy:

• Hisham Sati, Urs Schreiber, Equivariant Cohomotopy implies orientifold tadpole cancellation (arXiv:1909.12277)