nLab third stable homotopy group of spheres

Idea

The third stable homotopy group of spheres (the third stable stem) is the cyclic group of order 24 (cf. Toda 1961 p. 186):

(1)$$\array{ \pi_3^s &\simeq& \mathbb{Z}/24 \\ [h_{\mathbb{H}}] &\leftrightarrow& [1] }$$

where the generator $[1] \in \mathbb{Z}/24$ is represented by (the suspensions of) the quaternionic Hopf fibration $S^7 \overset{h_{\mathbb{H}}}{\longrightarrow} S^4$ (cf. Prop. below).

from SS21

Properties

Generator

Proposition

A generator of $\pi_3^s$, is represented by the suspension of the quaternionic Hopf fibration.

One would hope this could be cited directly from classical literature. But Toda 1962 makes the statement only for the 2-primary projection, Adams 1966 leaves it rather implicit, and also the review in Ravenel 2004 Thm. 1.13 still does not quite say it. Here is how to stitch this information together:

Proof

From Toda 1962 p. 186 we know that $\pi_3^s \simeq \mathbb{Z}_{/24}$. With this, Adams 1966 Thm. 1.5 implies that the J-homomorphism is surjective onto $\pi_3^s$. (Use here that, in Adams’s notation, $s = 1$, and then that the Bernoulli number $B_{2s} = B_2 = 1/6$ so that $B_{2s}/4s = 1/24$.) Finally, Adams 1966 §10 observes (stated more explicitly in Ravenel 2004 Thm. 1.13), that the image of the J-homomorphism in degree 3 is generated by the (suspensions $\nu$ of) the quaternionic Hopf fibration.

See also Kirdar 2021 §4.

As the third framed bordism group

Under the Pontrjagin-Thom isomorphism, identifying the stable homotopy groups of spheres with the bordism ring $\Omega^{fr}_\bullet$ of stably framed manifolds (see at MFr), the generator (1) is represented by the 3-sphere (with its left-invariant framing induced from the identification with the Lie group SU(2) $\simeq$ Sp(1) )

$$\array{ \pi_3^s & \simeq & \Omega_3^{fr} \\ [h_{\mathbb{H}}] & \leftrightarrow & [S^3_{fr=1}] \,. }$$

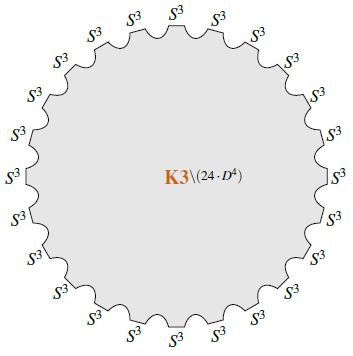
Moreover, the relation $24 \cdot [S^3_{Lie}] \,\simeq\, 0$ is represented by the bordism which is the complement of 24 open balls inside the K3-manifold (e.g. Wang-Xu 10, Sec. 2.6, Bauer 10, SP 17).

Via the fourth $(SU,fr)$-bordism group

Equivalently, the elements of $\pi_3^s \,\simeq\, \Omega^{fr}_3$ are detected by half the Todd classes of cobounding manifolds with special unitary group-tangential structure on their stable tangent bundle (elements of the MSUFr-bordism ring):

We have the following short exact sequence of the MSU-, MSUFr- and MFr-bordism rings (Conner-Floyd 66, p. 104)

(2)$$\array{ 0 \to & \Omega^{SU}_{8\bullet+4} & \overset{i}{\longrightarrow} & \Omega^{SU,fr}_{8\bullet+4} & \overset{\partial}{ \longrightarrow } & \Omega^{fr}_{8\bullet + 3} & \simeq & \pi^s_{8\bullet+3} \\ & \big\downarrow{}^{\tfrac{1}{2}\mathrlap{Td}} && \big\downarrow{}^{\tfrac{1}{2}\mathrlap{Td}} && \big\downarrow{}^{} && \big\downarrow{}^{e_{\mathbb{R}}} \\ 0 \to & \mathbb{Z} &\overset{\;\;\;\;\;}{\hookrightarrow}& \mathbb{Q} &\overset{\;\;\;\;}{\longrightarrow}& \mathbb{Q}/\mathbb{Z} &=& \mathbb{Q}/\mathbb{Z} }$$

which produces from half the Todd class of cobounding $(SU,fr)$-manifolds the KO-theoretic Adams e-invariant $e_{\mathbb{R}}$ (Adams 66, p. 39) of the boundary manifold in $\Omega^{fr}_{8k + 3} \simeq \pi^s_{8k+3}$. For $k = 0$ this detects the third stable homotopy group of spheres, by the following:

Proposition

(Adams 66, Example 7.17 and p. 46)

In degree 3, the KO-theoretic e-invariant $e_{\mathbb{R}}$ takes the value $\left[\tfrac{1}{24}\right] \in \mathbb{Q}/\mathbb{Z}$ on the quaternionic Hopf fibration $S^7 \overset{h_{\mathbb{H}}}{\longrightarrow} S^4$ and hence reflects the full third stable homotopy group of spheres:

$$\array{ \pi^s_3 & \underoverset{ \simeq }{ e_{\mathbb{R}} }{ \;\;\longrightarrow\;\; } & \mathbb{Z}/24 & \subset & \mathbb{Q}/\mathbb{Z} \\ [h_{\mathbb{H}}] &&\mapsto&& \left[\tfrac{1}{24}\right] }$$

while $e_{\mathbb{C}}$ sees only “half” of it (by Adams 66, Prop. 7.14).

Related concepts

• quaternionic Hopf fibration

• 24 branes transverse to K3

• first stable homotopy group of spheres

• second stable homotopy group of spheres

• seventh stable homotopy group of spheres

References

The original computation:

• Vladimir Abramovich Rokhlin, On a mapping of the $(n+3)$-dimensional sphere into the $n$-dimensional sphere, (Russian) Doklady Akad. Nauk SSSR (N.S.) 80, (1951). 541–544

with a mistake (in the unstable range) corrected in

• Vladimir Abramovich Rokhlin, New results in the theory of four-dimensional manifolds, (Russian) Doklady Akad. Nauk SSSR (N.S.) 84, (1952). 221–224.

French translation:

• Lucien Guillou, Alexis Marin (eds.): A la Recherche de la Topologie Perdue: I. Du côté de chez Rohlin. II. Le côté de Casson, Progress in Mathematics 62, Birkhäuser Boston (1985) [ISBN:0817633294, 9780817633295]

Further early discussion, as part of a comprehensive analysis:

• Hirosi Toda; p. 186 of: Composition Methods in Homotopy Groups of Spheres, Annals of Mathematics Studies 49, Princeton University Press (1962) [doi:10.1515/9781400882625, jstor:j.ctt1bgzb5t]

Review:

• Guozhen Wang, Zhouli Xu, Section 2.6 of: A survey of computations of homotopy groups of Spheres and Cobordisms, 2010 (pdf)

In relation to the J-homomorphism:

• John Adams; Thm. 1.6 in: On the groups $J(X)$ IV, Topology 5 1 (1966) 21–71 [doi:10.1016/0040-9383(66)90004-8, pdf]

• Doug Ravenel; Thm 1.1.13 in: Complex cobordism and stable homotopy groups of spheres, Academic Press Orland (1986) reprinted as: AMS Chelsea Publishing 347 (2004) [ISBN:978-0-8218-2967-7, webpage, pdf]

See also:

• Mehmet Kirdar: On the First, the Second and the Third Stems of the Stable Homotopy Groups of Spheres [arXiv:2107.06103]

More on the computation via the framed cobordism ring and the K3-manifold giving the cobordism that witnesses the order of 24:

• Tilman Bauer, answer to: third stable homotopy group of spheres via geometry?, 2010 (MO:a/44885)

• Chris Schommer-Pries, answer to: Nilpotence of the stable Hopf map via framed cobordism, 2017 (MO:a/218053)

Via immersions of 3-spheres into Euclidean 4-space

• A. Szűcs, Two Theorems of Rokhlin, Journal of Mathematical Sciences 113, 888–892 (2003) (doi:10.1023/A:1021208007146)

• Tobias Ekholm, Masamichi Takase, Singular Seifert surfaces and Smale invariants for a family of 3-sphere immersions, Bulletin of the London Mathematical Society 43 (2011) 251–266 (arXiv:0903.0238)

Discussion of geometric string bordism in degreee 3 as a means to speak (via the Pontryagin-Thom theorem) about the third stable homotopy group of spheres:

• Domenico Fiorenza, Eugenio Landi, Integrals detecting degree 3 string cobordism classes [arXiv:2209.12933]

• Domenico Fiorenza, String bordism invariants in dimension 3 from $U(1)$-valued TQFTs, talk at QFT and Cobordism, CQTS (Mar 2023) [web]