nLab 24 branes transverse to K3

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Discuss this page |
Contents

Context

String theory

Ingredients

Critical string models

Extended objects

Topological strings

Backgrounds

Phenomenology

Contents

Idea

Several classes of string theory vacua require the presence of exactly 24 branes of codimension 4 transverse to a K3-surface-fiber; this happens notably:

In both cases the condition arises as a kind of tadpole cancellation-condition, where the charge of the 24 branes in the compact K3-fiber space, which naively would be 24 in natural units, cancels out to zero, due to some subtle effect.

Despite the superficial similarity, this subtle effect is, at the face of it, rather different in the two cases:

An argument that these two different-looking mechanisms are in fact equivalent, under suitable duality in string theory, is given in Braun-Brodie-Lukas-Ruehle 18, Sec. III, following detailed analysis due to Aspinwall-Morrison 97.

In F-theory on K3

In passing from M-theory to type IIA string theory, the locus of any Kaluza-Klein monopole in 11d becomes the locus of D6-branes in 10d. The locus of the Kaluza-Klein monopole in turn (as discussed there) is the locus where the S A 1S^1_A-circle fibration degenerates. Hence in F-theory this is the locus where the fiber of the S A 1×S B 1S^1_A \times S^1_B-elliptic fibration degenerates to the nodal curve. Since the T-dual of D6-branes are D7-branes, it follows that D7-branes in F-theory “are” the singular locus of the elliptic fibration.

Now, considering F-theory on K3, an elliptically fibered complex K3-surface

T ⟶ K3 ↓ ℂℙ 1 \array{ T &\longrightarrow& K3 \\ && \downarrow \\ && \mathbb{C}\mathbb{P}^1 }

may be parameterized via the Weierstrass elliptic function as the solution locus of the equation

y 2=x 3+f(z)x+g(z) y^2 = x^3 + f(z) x + g(z)

for x,y,z∈ℂℙ 1x,y,z \in \mathbb{C}\mathbb{P}^1, with ff a polynomial of degree 8 and gg of degree twelve. The j-invariant of the complex elliptic curve which this parameterizes for given zz is

j(τ(z))=4(24f) 327g 2+4f 3. j(\tau(z)) = \frac{4 (24 f)^3}{27 g^2 + 4 f^3} \,.

The poles j→∞j\to \infty of the j-invariant correspond to the nodal curve, and hence it is at these poles that the D7-branes are located.

homotopy pasting diagram exhibiting the homotopy Whitehead integral
from SS21

Since the order of the poles is 24 (the polynomial degree of the discriminant Δ=27g 2+4f 3\Delta = 27 g^2 + 4 f^3, see at elliptically fibered K3-surface – singular points) there are necessarily 24 D7-branes (Sen 96, page 5, Lerche 99, p. 6 , see also Morrison 04, sections 8 and 17, Denef 08, around (3.41), Douglas-Park-Schnell 14).

Notice that the net charge of these 24 D7-branes is supposed to vanish, due to S-duality effects (e.g. Denef 08, below (3.41)).

In IIA-theory on K3

Under T-duality the above discussion in F-theory translates to 24 D6-branes in type IIA string theory on K3 (Vafa 96, Footnote 2 on p. 6).

In HET-theory on K3

In heterotic string theory KK-compactified on K3 with vanishing gauge fields-instanton number, the existence of exactly 24 NS5-branes is implied by the Green-Schwarz mechanism: This requires that the 3-flux density H 3H_3 measuring the NS5-brane charge satisfies dH 3=trac12p 1(∇) d H_3 = \trac{1}{2} p_1(\nabla); and using that on K3 we have ∫ K312p 1(∇)=∫ K3χ 4(∇)=χ 4[K3]=24\int_{K3} \tfrac{1}{2} p_1(\nabla) = \int_{K3} \chi_4(\nabla) = \chi_4[K3] = 24 this implies, with Stokes' theorem, that the H 3H_3-flux through the 3-spheres around transversal NS5-brane-punctures of the K3 equals 24 (e.g. Schwarz 96, around p. 50, Aspinwall-Morrison 97, Sec. 4-5, Johnson 98, p. 30, Braun-Brodie-Lukas-Ruehle 18, Section III.A, Choi-Kobayashi 19, Sec. 1.1).

The duality of this HET-phenomenon with that in F-theory above is discussed in Braun-Brodie-Lukas-Ruehle 18, Section III.

Under Hypothesis H

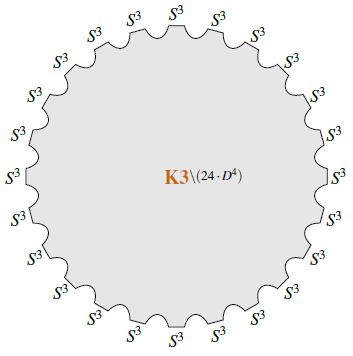
The vanishing of the Euler characteristic of K3 after cutting out the complement of 24 points is precisely the mechanism which witnesses the order 24 of the third stable homotopy group of spheres, seen under Pontryagin's theorem as the existence of a framed cobordism K3∖24⋅D 4K3 \setminus 24 \cdot D^4 between 24 3-spheres:

from SS21

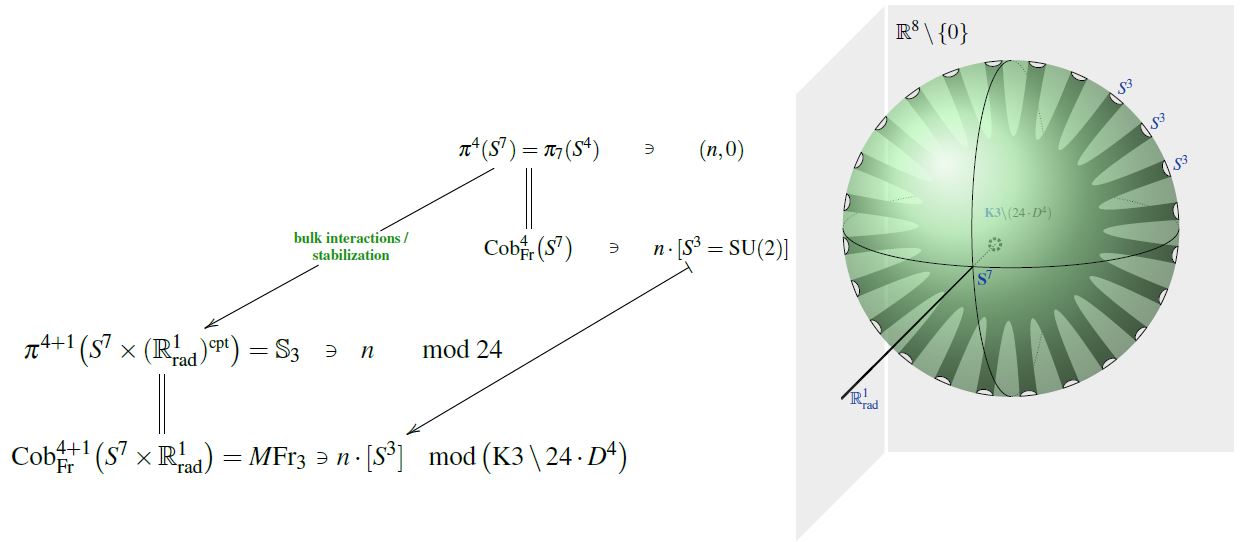
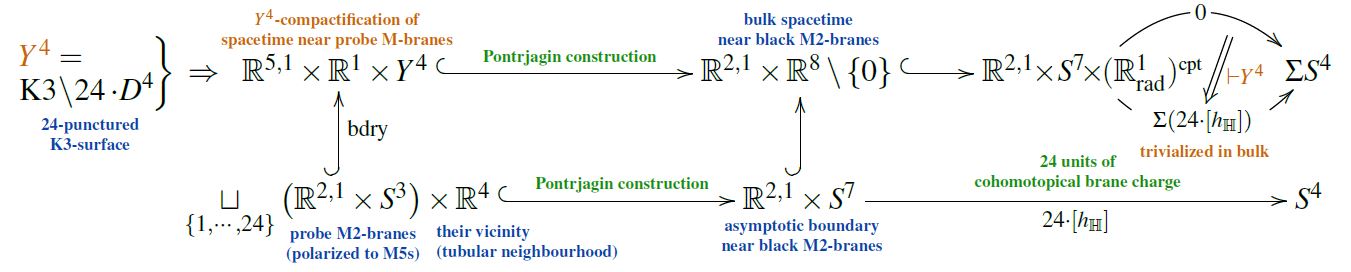
This relates the number of 24 branes transverse on K3 to Hypothesis H:

from SS21

References

In F-theory

Discussion in F-theory via the Kodeira classification of elliptically fibered K3s:

In HET-theory

Discussion in heterotic string theory via the Green-Schwarz mechanism on K3 (see also at small instantons):

In F- and HET-theory

Joint discussion in F- and dual HET-theory:

Swampland cobordism conjecture

The swampland cobordism conjecture is the hypothesis that consistency of vacua in string theory/M-theory/F-theory (hence their being in the “landscape” instead of the “swampland”) requires (undefined) stringy/quantum gravity-analogs of cobordism groups to vanish:

Relation to topological K-theory and D-brane charge quantization in K-theory:

Review:

A more concrete consequence of this conjecture is claimed (McNamara & Vafa 2019, Sec. 5.2, 2nd paragr.) to be the statement that – paraphrasing/extrapolating somewhat (in line with Blumenhagen & Cribiori 2022; Blumenhagen et al. 2023; Blumenhagen 2023, p. 23): Certain topological brane charges are quantized in Cobordism cohomology; so that, in particular tadpole cancellation of brane charges is to happen in Cobordism cohomology. This kind of statement is also discussed, as a consequence of Hypothesis H, in (see p. 83):

Last revised on July 23, 2022 at 17:42:21. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (3 revisions) Cite Print Source