Schreiber Lift of fractional D-brane charge to equivariant Cohomotopy theory

Redirected from "The image of the Burnside ring in the Representation ring".

An article that we have written:

Abstract. The lift of K-theoretic D-brane charge to M-theory was recently hypothesized to land in Cohomotopy cohomology theory. To further check this $\,$ Hypothesis H, here we explicitly compute the constraints on fractional D-brane charges at ADE-orientifold singularities imposed by the existence of lifts from equivariant K-theory to equivariant Cohomotopy theory, through Boardman's comparison homomorphism. We check the relevant cases and find that this condition singles out precisely those fractional D-brane charges which do not take irrational values, in any twisted sector. Given that the possibility of irrational D-brane charge has been perceived as a paradox in string theory, we conclude that Hypothesis H serves to resolve this paradox.

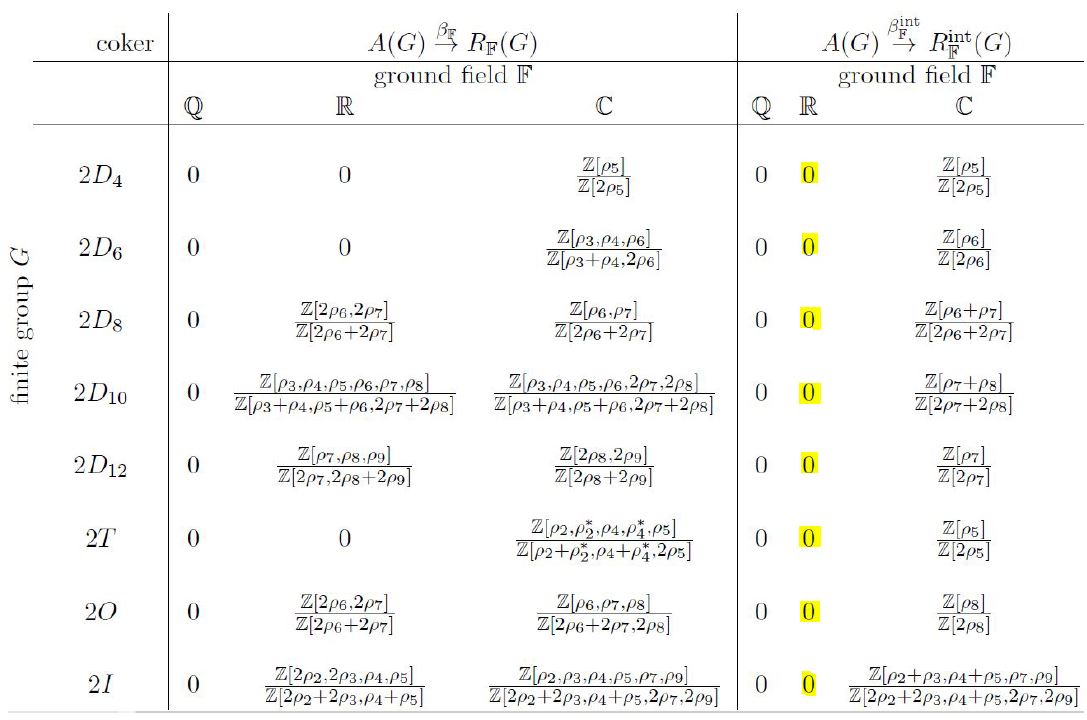
Concretely, we first explain that the Boardman homomorphism, in the present case, is the map from the Burnside ring to the representation ring of the singularity group given by forming virtual permutation representations. Then we describe an explicit algorithm that computes the image of this comparison map for any finite group. We run this algorithm for binary Platonic groups, hence for finite subgroups of SU(2); and we find explicitly that for the three exceptional subgroups (2T, 2O, 2I) and for the first few cyclic and binary dihedral subgroups the comparison morphism surjects precisely onto the sub-lattice of the real representation ring spanned by the non-irrational characters.

Related articles

Related talks

Last revised on December 17, 2020 at 15:30:34. See the history of this page for a list of all contributions to it.